• K-Nearest Neighbor je jeden z nejjednodušších algoritmů založených na strojovém učení o metodě supervidovaného učení.
• Algoritmus K-NN předpokládá podobnost mezi novými případy / daty a dostupnými případy a zařazuje nový případ do kategorie, která se nejvíce podobá dostupným kategoriím.

K-NN algoritmus ukládá všechna dostupná data a klasifikuje nový datový bod na základě podobnosti. To znamená, že když se objeví nová data, lze je snadno zařadit do kategorie sady vrtů pomocí algoritmu K-NN.

• Algoritmus K-NN lze použít pro regresi i klasifikaci, ale většinou se používá pro klasifikační problémy.
• K-NN je neparametrický algoritmus, což znamená nevytváří žádný předpoklad o podkladových datech.
• Nazývá se také algoritmus líného žáka, protože se nenaučí z tréninkové sady okamžitě, místo toho uloží datovou sadu a v době klasifikace provede akce na datové sadě.
• Algoritmus KNN ve fázi tréninku datovou sadu pouze uloží a když získá nová data, klasifikuje tato data do kategorie, která je hodně podobná novým datům.
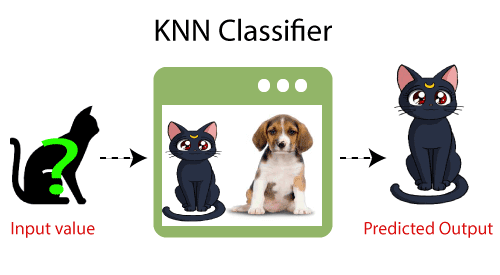
• Příklad: Předpokládejme, že máme obraz tvora, který vypadá podobně jako kočka a pes, ale chceme vědět, zda je to kočka nebo pes. Pro tuto identifikaci tedy můžeme použít algoritmus KNN, protože pracuje na míře podobnosti. Náš model KNN najde podobné vlastnosti nové datové sady jako obrázky koček a psů a na základě nejpodobnějších funkcí jej zařadí do kategorie koček nebo psů.

Proč potřebujeme algoritmus K-NN?

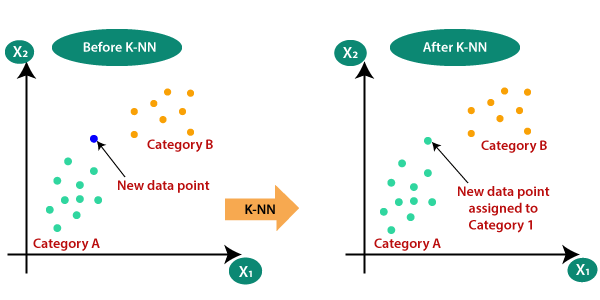
Předpokládejme, že existují dvě kategorie, tj. Kategorie A a Kategorie B, a máme nový datový bod x1, takže tento datový bod bude ležet ve které z těchto kategorií. K vyřešení tohoto typu problému potřebujeme algoritmus K-NN. S pomocí K-NN můžeme snadno identifikovat kategorii nebo třídu konkrétní datové sady. Zvažte následující diagram:

Jak funguje K-NN?

Fungující K-NN lze vysvětlit na základě níže uvedený algoritmus:

• Krok 1: Vyberte počet K sousedů
• Krok 2: Vypočítejte euklidovskou vzdálenost K počtu sousedů
• Krok 3: Vezměte K nejbližší sousedy podle vypočtené euklidovské vzdálenosti.
• Krok 4: Mezi těmito k sousedy spočítejte počet datových bodů v každé kategorii.
• Krok 5: Přiřaďte nové datové body k té kategorii, pro kterou je maximální počet sousedů.
• Krok 6: Náš model je připraven.

Předpokládejme, že máme nový datový bod a musíme jej zařadit do požadované kategorie. Zvažte následující obrázek:

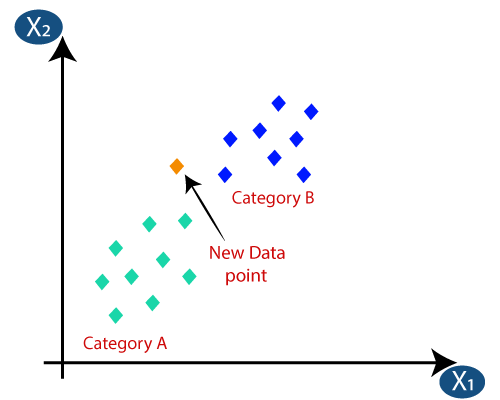
• Nejprve zvolíme počet sousedů, takže zvolíme k = 5.
• Dále vypočítáme euklidovskou vzdálenost mezi datovými body. Euklidovská vzdálenost je vzdálenost mezi dvěma body, kterou jsme již studovali v geometrii. Lze jej vypočítat jako:

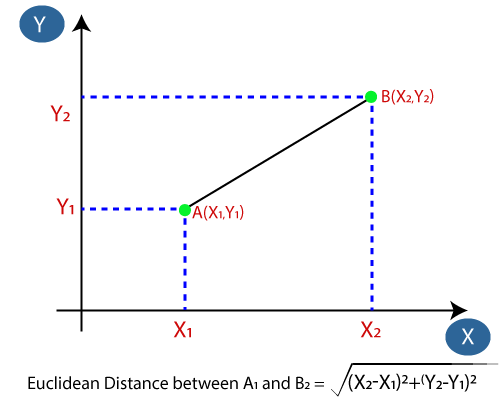
• Výpočetem euklidovské vzdálenosti jsme dostali nejbližší sousedy, jako tři nejbližší sousedy v kategorii A a dva nejbližší sousedy v kategorii B. Zvažte následující obrázek:

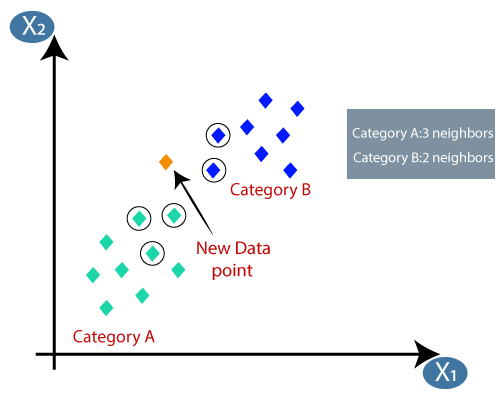
• Jak vidíme, 3 nejbližší sousedé jsou z kategorie A, proto tento nový datový bod musí patřit do kategorie A.

Jak vybrat hodnotu K v algoritmu K-NN?

Níže jsou uvedeny některé body k pamatujte při výběru hodnoty K v algoritmu K-NN:

• Neexistuje žádný konkrétní způsob, jak určit nejlepší hodnotu pro „K“, takže musíme najít některé hodnoty, abychom našli nejlepší z nich. Nejvýhodnější hodnota pro K je 5.
• Velmi nízká hodnota pro K, jako je K = 1 nebo K = 2, může být hlučná a vést k účinkům odlehlých hodnot v modelu.
• Velké hodnoty pro K jsou dobré, ale může najít určité potíže.

Výhody algoritmu KNN:

• Implementace je jednoduchá.
• Je robustní vůči hlučným tréninkovým datům.
• Může být efektivnější, pokud jsou tréninková data velká.

Nevýhody algoritmu KNN:

• Vždy je třeba určit hodnotu K, která může být někdy složitá.
• Náklady na výpočet jsou vysoké kvůli výpočtu vzdálenosti mezi datovými body pro všechny tréninkové vzorky .

Implementace algoritmu KNN v Pythonu

Abychom implementovali algoritmus K-NN v Pythonu, použijeme stejný problém a soubor dat, který jsme použili v Logistická regrese. Ale zde vylepšíme výkon modelu. Níže je uveden popis problému:

Problém s algoritmem K-NN: Existuje společnost výrobce automobilů, která vyrobila nové SUV.Společnost chce dát reklamy uživatelům, kteří mají zájem o koupi tohoto SUV. Takže pro tento problém máme datovou sadu, která obsahuje více informací o uživateli prostřednictvím sociální sítě. Datová sada obsahuje spoustu informací, ale odhadovaný plat a věk, který budeme brát v úvahu pro nezávislou proměnnou, a zakoupená proměnná pro závislou proměnnou. Níže je uveden soubor dat:

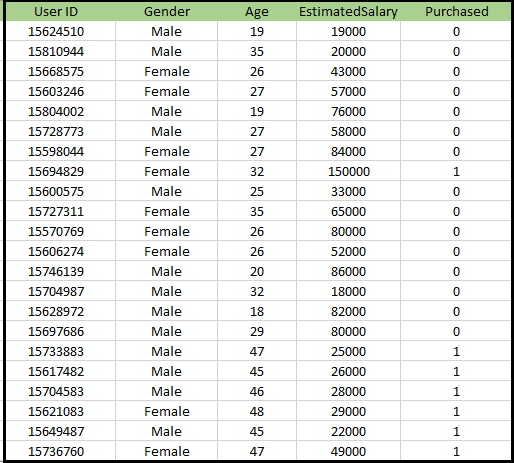
Kroky k implementaci algoritmu K-NN:

• Krok předběžného zpracování dat
• Přizpůsobení algoritmu K-NN tréninkové sadě
• Predikce výsledku testu
• Přesnost testu (Creation of Confusion matrix)
• Vizualizace výsledku testovací sady.

Krok předběžného zpracování dat:

Krok předběžného zpracování dat zůstane přesně stejný jako u logistické regrese. Níže je uveden kód za to:

Provedením výše uvedeného kódu se náš datový soubor importuje do našeho programu a dobře se předzpracuje. Po změně měřítka funkce bude náš testovací datový soubor vypadat takto:

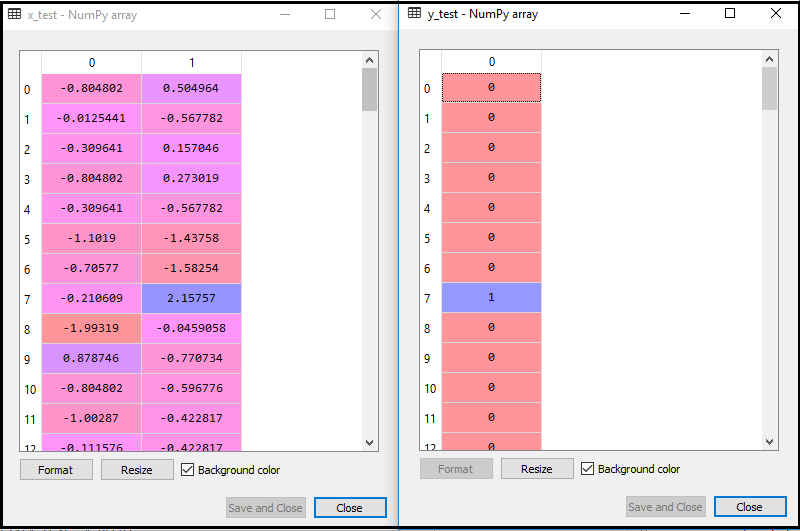
Z výše uvedeného výstupu im věku vidíme, že naše data jsou úspěšně škálována.

• Přizpůsobení klasifikátoru K-NN tréninkovým datům:
  Nyní přizpůsobíme klasifikátor K-NN tréninkovým datům. K tomu importujeme třídu KNe NeighborsClassifier knihovny Sklearn Neighbors. Po importu třídy vytvoříme objekt Classifier třídy. Parametr této třídy bude
  • n_ne Neighbors: Chcete-li definovat požadované sousedy algoritmu. Obvykle to trvá 5.
  • metric = „minkowski“: Toto je výchozí parametr a určuje vzdálenost mezi body.
  • p = 2: Je to ekvivalent standardu Euklidovská metrika.

  A potom přizpůsobíme klasifikátor tréninkovým datům. Níže je uveden jeho kód:

Výstup: Provedením výše uvedeného kódu získáme výstup jako:

• Predikce výsledku testu: Abychom mohli předpovědět výsledek testovací sady, vytvoříme vektor y_pred stejně jako v Logistické regrese. Níže je uveden kód:

Výstup:

Výstup pro výše uvedený kód bude:

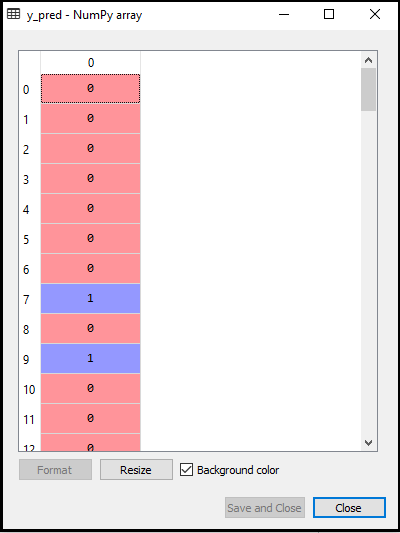
• Vytvoření matice zmatku:
  Nyní vytvoříme matici zmatku pro náš model K-NN, abychom viděli přesnost klasifikátoru. Níže je uveden její kód:

Ve výše uvedeném kódu jsme importovali funkci confusion_matrix a nazvali ji pomocí proměnné cm.

Výstup: Provedením výše uvedeného kódu získáme matici uvedenou níže:

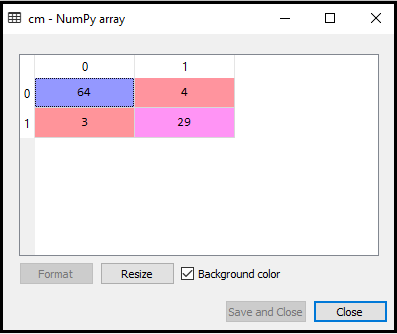
Na obrázku výše vidíme existuje 64 + 29 = 93 správných předpovědí a 3 + 4 = 7 nesprávných předpovědí, zatímco v Logistické regrese bylo 11 nesprávných předpovědí. Můžeme tedy říci, že výkon modelu se zlepšuje pomocí algoritmu K-NN.

• Vizualizace výsledku Training set:
  Nyní si vizualizujeme výsledek tréninkové sady pro K -NN model. Kód zůstane stejný jako v Logistické regrese, kromě názvu grafu. Níže je uveden jeho kód:

Výstup:

Provedením výše uvedeného kódu získáme následující graf:

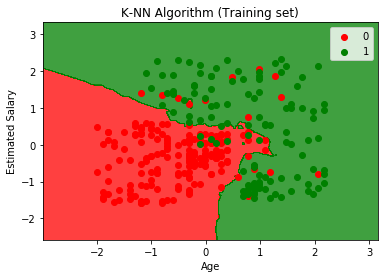
Výstupní graf se liší od grafu, ke kterému došlo v logistické regrese. Lze to pochopit v následujících bodech:

• Jak vidíme, graf ukazuje červený bod a zelené body. Zelené body jsou pro proměnnou Zakoupeno (1) a Červené body pro Nekoupeno (0).
• Graf zobrazuje nepravidelnou hranici namísto zobrazení jakékoli přímky nebo křivky, protože se jedná o algoritmus K-NN, tj. nalezení nejbližšího souseda.
• Graf klasifikoval uživatele do správných kategorií, protože většina uživatelů, kteří si SUV nekoupili, jsou v červené oblasti a uživatelé, kteří si SUV koupili, jsou v zelené oblasti.
• Graf ukazuje dobrý výsledek, ale přesto jsou v červené oblasti zelené body a v zelené oblasti červené body. To však není velký problém, protože provedením tohoto modelu se zabrání problémům s nadměrným vybavováním.
• Proto je náš model dobře vyškolený.
• Vizualizace výsledku testovací sady:
  Po zaškolení modelu nyní otestujeme výsledek vložením nové datové sady, tj. Testovací datová sada. Kód zůstává stejný až na některé drobné změny: například x_train a y_train budou nahrazeny x_test a y_test.
  Níže je uveden kód:

Výstup:

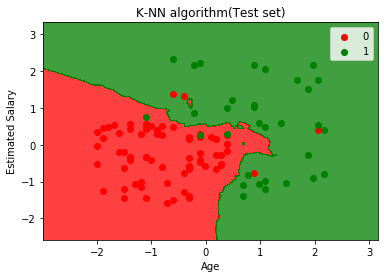
Výše uvedený graf ukazuje výstup pro testovací datovou sadu. Jak vidíme v grafu, předpokládaný výstup je dobrý dobré, protože většina červených bodů je v červené oblasti a většina zelených bodů je v zelené oblasti.

Existuje však několik zelených bodů v červené oblasti a několik červených bodů v zelené oblasti. Toto jsou nesprávná pozorování, která jsme pozorovali v matici zmatků (7 Nesprávný výstup).