Když vystřelíte střelu pod úhlem # theta # od vodorovné roviny, počáteční rychlost střely mít svislou a vodorovnou složku.

# {(v_ (0x) = v_0 * cos (theta)), (v_ (0y) = v_0 * sin (theta)):} #

Za účelem určení maximální výška dosažená projektilem během jeho letu, musíte se podívat na svislou složku jeho pohybu.

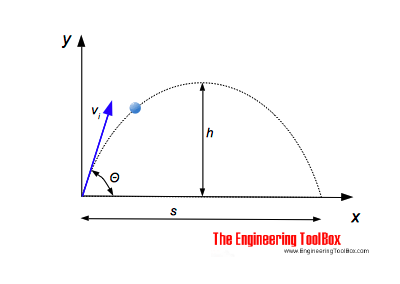
Pohyb střely je vertikálně ovlivněn gravitací. To znamená, že při maximální výšce bude vertikální složka počáteční rychlosti nulová.

Projektil zpomalí na své cestě do maximální výšky, úplně se zastaví v maximální výšce a poté zahájí svůj volný pád sestup k zemi.

Pokud použijete svislou složku počáteční rychlosti, můžete napsat

#underbrace (v_ „h max“ ^ 2) _ (color (blue) („= 0“) )) = v_text (0y) ^ 2 – 2 * g * h_ „max“ #

To odpovídá

#v_ (0y) ^ 2 = 2 * g * h_ „max“ #

Maximální výška dosažená projektilem bude tedy

#h_ „max“ = v_ (0y) ^ 2 / (2 * g) = (v_0 * sin (theta)) ^ 2 / (2 * g) #

#h_ „max“ = barva (zelená) ((v_0 ^ 2 * sin ^ 2 (theta)) / (2 * g) ) #