MATH 1314: College Algebra (Čeština)
Zatímco vertikální asymptoty popisují chování grafu, protože výstup je velmi velký nebo velmi malý, horizontální asymptoty pomáhají popsat chování grafu jako vstup je velmi velký nebo velmi malý. Připomeňme, že koncové chování polynomu bude zrcadlit chování vedoucího členu. Stejně tak bude koncové chování racionální funkce odrážet poměr hlavních podmínek funkcí čitatele a jmenovatele.
Při kontrole horizontálních asymptot existují tři odlišné výsledky:
Případ 1: Pokud je stupeň jmenovatele > stupeň čitatele, existuje vodorovná asymptota na y = 0.

Případ 2: Pokud stupeň jmenovatele < stupeň čitatele o jeden, dostaneme šikmou asymptotu.

Všimněte si, že zatímco graf racionální funkce nikdy nepřekročí svislou asymptotu, graf může nebo nemusí překročit vodorovnou nebo šikmou plochu jako ymptote. I když graf racionální funkce může mít mnoho vertikálních asymptot, bude mít graf nejvýše jednu horizontální (nebo šikmou) asymptotu.
Je třeba poznamenat, že pokud je stupeň čitatele větší než stupeň jmenovatele o více než jeden, bude koncové chování grafu napodobovat chování redukované frakce koncového chování. Například kdybychom měli funkci
s chováním na konci
konečné chování grafu bude vypadat podobně jako u rovnoměrného polynomu s kladným vedoucím koeficientem.
Obecná poznámka: Horizontální asymptoty racionálních funkcí
Horizontální asymptota racionální funkce může být určeno pohledem na stupně čitatele a jmenovatele.
- Stupeň čitatele je menší než stupeň jmenovatele: vodorovná asymptota na y = 0.
- Stupeň čitatele je větší než stupeň jmenovatele jedním: žádný horizontální asymptot; šikmá asymptota.
- Stupeň čitatele se rovná stupni jmenovatele: vodorovná asymptota při poměru hlavních koeficientů.
Příklad 9: Identifikace horizontálních a vertikálních asymptot
Najděte horizontální a vertikální asymptoty funkce
Solution
Nejprve si všimněte, že tato funkce nemá žádné společné faktory, takže neexistují žádné potenciální vyměnitelné diskontinuity.
Funkce bude mít vertikální asymptoty, když je jmenovatel nulový, což způsobí, že funkce nebude definována. Jmenovatel bude nula na x = 1, -2, text {a} 5 \, což znamená vertikální asymptoty na těchto hodnotách.
Čitatel má stupeň 2, zatímco jmenovatel má stupeň 3. Protože stupeň Jmenovatel je větší než stupeň čitatele, jmenovatel bude růst rychleji než čitatel, což způsobí, že výstupy budou mít tendenci k nule, jak se vstupy zvětšují, a tak jako xto pm infty, fleft (xright) na 0 \. Tato funkce bude mít vodorovnou asymptotu na y = 0 \.
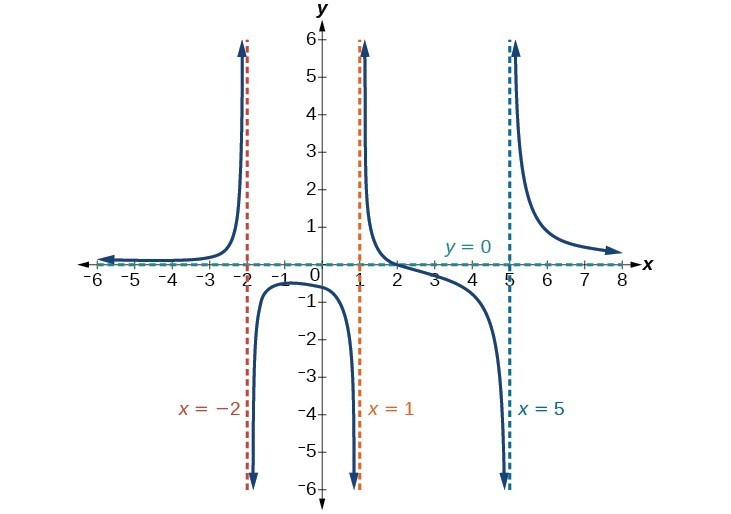
Obrázek 15
Obecná poznámka: Zachycení racionálních funkcí
Racionální funkce bude mít průnik y, když je vstup nula, pokud je funkce definována na nulu. Racionální funkce nebude mít průnik y, pokud funkce není definována na nule.
Podobně bude mít racionální funkce na průchodech x průsečíky, které způsobí, že výstup bude nulový. Vzhledem k tomu, že zlomek se rovná nule pouze v případě, že čitatel je nula, mohou se x-průsečíky vyskytnout pouze v případě, že se čitatel racionální funkce rovná nule.
Zkuste to 7
Vzhledem k reciproční funkci na druhou, která je posunuta o 3 jednotky doprava a dolů o 4 jednotky, zapište to jako racionální funkci. Poté najděte průsečíky x– a y a horizontální a vertikální asymptoty.
Řešení