Řešení
ColligativeProperties
Deprese tlaku páry
Fyzikální vlastnosti lze rozdělit do dvou kategorií. Rozsáhlé vlastnosti (například hmotnost a objem) závisí na velikosti vzorku. Intenzivní vlastnosti (například hustota a koncentrace) jsou charakteristické vlastnosti látky; nezávisí na velikosti zkoumaného vzorku. Tato část představuje třetí kategorii, která je podmnožinou intenzivních vlastností systému. Tuto třetí kategorii, známou jako colligativeproperties, lze použít pouze u řešení. Podle definice je jednou z vlastností řešení kogrativní vlastnost, pokud závisí pouze na poměru počtu částic rozpustné látky a rozpouštědla v roztoku, nikoli na totožnosti rozpuštěné látky.
Velmi málo fyzických vlastností řešení je inteligenčních vlastností. Jako příklad této omezené sady fyzikálních vlastností uvažujme, co se stane s tlakem páry rozpouštědla, když přidáme rozpuštěnou látku k vytvoření roztoku. Definujeme Po jako tlak páry čisté kapaliny rozpouštědlo ![]() a P jako tlak páry v rozpouštědle po přidání rozpuštěné látky.
a P jako tlak páry v rozpouštědle po přidání rozpuštěné látky.
Po = tlak páry čisté kapaliny nebo rozpouštědla
P = tlak páry rozpouštědla v roztoku
Když je teplota kapaliny pod jejím bodem varu Bod, můžeme předpokládat, že jediné molekuly, které mohou uniknout z kapaliny za vzniku plynu, jsou ty, které leží poblíž povrchu kapaliny.
Když je do rozpouštědla přidána rozpuštěná látka, některé z těchto solutemolekul zabírají prostor poblíž povrchu kapaliny, jak je znázorněno na obrázku níže. Když je rozpuštěná látka rozpuštěna v rozpouštědle, snižuje se počet molekul rozpouštědla v blízkosti povrchových ploch a tlak par rozpouštědla klesá.

To nemá žádný vliv na rychlost, jakou molekuly rozpouštědla v plynné fázi kondenzují za vzniku kapaliny. Snižuje se však na té úrovni, při které molekuly rozpouštědla v kapalině mohou uniknout do plynné fáze. Ve výsledku by měl být tlak par rozpouštědla unikajícího z roztoku menší než tlak páry čistého rozpouštědla.
| P | < | Po | ||
| tlak par rozpouštědlo nad roztokem |
tlak par čistého rozpouštědla |
Mezi lety 1887 a 1888 Francois-Marie Raoult ukázala, že tlak páry roztoku je se rovná molárnímu podílu rozpouštědla krát tlak par čisté kapaliny.
| P | = | Csolvent Po | ||||
| tlak par rozpouštědla nad řešením |
tlak par čistého čistého rozpouštědla |
Tato rovnice, která je známá jako Raoultův zákon, je snadno pochopitelná. Když je rozpouštědlo čisté a molární frakce rozpouštědla je rovna 1, P se rovná Po. Jak se molární podíl rozpouštědla zmenšuje , bude tlak páry unikajícího z roztoku také menší.
Předpokládejme prozatím, že rozpouštědlo je jedinou složkou roztoku, která je dostatečně těkavá, aby měla měřitelný tlak par. Pokud je to pravda, tlak par roztoku se bude rovnat tlaku par rozpouštědla unikajícího z roztoku. Raoultův zákon naznačuje, že rozdíl mezi tlakem par čistého rozpouštědla a roztokem se zvyšuje se snižováním molárního podílu rozpouštědla.
Změna tlaku par, ke které dochází, když se do rozpouštědla přidá asolut proto koligativní vlastnost. Pokud to závisí na molárním podílu rozpuštěné látky, pak to musí záviset na poměru počtu částic rozpuštěné látky k rozpouštědlu v roztoku, ale ne na identitě rozpuštěné látky.
![]()
Zvýšení bodu varu a pokles bodu mrznutí
Následující obrázek ukazuje důsledky skutečnosti, že rozpustné látky snižují tlak par rozpouštědla. spojovací body B a C v tomto fázovém diagramu obsahují kombinace teploty a tlaku, při nichž jsou čisté rozpouštědlo a jeho páry v rovnováze. Každý bod na tomto řádku proto popisuje tlak par čisticího rozpouštědla při dané teplotě. Tečkovaná čára na tomto obrázku popisuje vlastnosti Roztoku získaného rozpuštěním absolutního množství v rozpouštědle.Při jakékoli dané teplotě je tlak páry rozpouštědla unikajícího z roztoku menší než tlak páry čistého rozpouštědla. Tečkovaná čára proto leží pod plnou čarou.
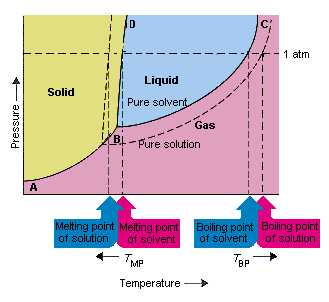
Pokles tlak par rozpouštědla, ke kterému dochází, když se k rozpouštědlu přidá rozpuštěná látka, způsobí zvýšení bodu varu a snížení teploty tání roztoku.
Podle tohoto obrázku nemůže roztok vřít při stejné teplotě jako čisté rozpouštědlo. Pokud tlak par rozpouštědlo unikající z roztoku je menší než tlak páry čistého rozpouštědla při jakékoli dané teplotě, musí se roztok zahřát na vyšší teplotu, než začne vřít. Snížení tlaku par rozpouštědla, ke kterému dochází, když se použije k vytvoření roztoku, proto zvyšuje bod varu kapaliny.
Když byly zavedeny fázové diagramy, byl trojitý bod definován jako jediná kombinace teploty a tlaku, při které může současně existovat plyn, kapalina a pevná látka. Obrázek výše ukazuje že trojný bod roztoku se vyskytuje při nižší teplotě než trojný bod čistého rozpouštědla. Samotná změna trojitého bodu není důležitá. Výsledkem však bude změna teploty, při které roztok zamrzne nebo se roztaví. proč, musíme vypadat opatrně plně na linii, která odděluje pevnou a kapalnou oblast ve phasediagramu. Tato čára je téměř vertikální, protože tání látky není příliš citlivé na tlak.
Přidání rozpuštěné látky k rozpouštědlu nezmění způsob, jakým bod tání závisí na tlaku. Linka, která odděluje pevné a kapalné oblasti roztoku, je tedy rovnoběžná s linií, která slouží stejné funkci pro čisté rozpouštědlo . Tato čára však musí projít trojným bodem pro roztok. Snížení trojného bodu, ke kterému dochází, když je asolut rozpuštěn v rozpouštědle, tedy snižuje teplotu tání roztoku.
Obrázek výše ukazuje, jak změna tlaku par, ke které dochází, když se rozpustí rozpuštěná látka v rozpouštědle, vede ke změnám teploty tání a teploty varu rozpouštědla. Protože změna tlaku par je koligativní vlastnost, která závisí pouze na relativním počtu částic rozpuštěné látky a rozpouštědla , změny bodu varu a teploty tání rozpouštědla jsou také koligativní vlastnosti.
![]()
Výpočty ColligativeProperties
Nejlepší cesta k démonům Významem inteligenčních vlastností je zkoumat důsledky Raoultova zákona. Zjistilo se, že tlak par rozpouštědla unikajícího z roztoku je úměrný molárnímu podílu rozpouštědla.
P = CsolventPo
Tlak par rozpouštědla však není koligativní vlastností. Mezi koligativní vlastnosti roztoku lze zahrnout pouze změnu tlaku par, která nastane, když se do rozpouštědla přidá rozpuštěná látka.
Protože tlak je stavová funkce, lze změnu tlaku páry rozpouštědla, ke které dojde, když se do rozpouštědla přidá rozpuštěná látka, definovat jako rozdíl mezi tlakem páry čistého rozpouštědla a tlakem páry rozpouštědla unikající z řešení.
P = Po – P
Dosazením Raoultova zákona do této rovnice získáte následující výsledek.
P = Po – Csolvent Po = (1 – Csolvent) Po
Tuto rovnici lze zjednodušit zapamatováním si vztahu mezi molárním zlomkem rozpuštěné látky a molární frakcí rozpouštědla.
Csolute + Csolvent = 1
Dosazením tohoto vztah do rovnice, která definuje Pgives, dává další formu Raoultova zákona.
P = CsolutePo
Tato rovnice nám připomíná, že změna tlaku par rozpouštědla, ke které dochází, když se k rozpouštědlu přidá rozpuštěná látka, je úměrná molárnímu podílu rozpuštěné látky. Když je moresolute rozpuštěn v rozpouštědle, tlak par rozpouštědla klesá a změna tlaku par rozpouštědla se zvyšuje.
Protože změny bodu varu rozpouštědla (TBP), ke kterým dochází při přidání rozpuštěné látky k rozpouštědlu, jsou důsledkem změn tlaku par rozpouštědla, velikost změny bodu varu je také úměrná k molekulové frakci rozpuštěné látky.
![]() TBP = kbsolute
TBP = kbsolute
Ve zředěných roztocích je molární podíl rozpuštěné látky úměrný molalitě roztoku, jak je uvedeno v obrázek níže.

Rovnice, která popisuje velikost varu pointelevace, ke kterému dochází při přidání rozpuštěné látky do rozpouštědla, se proto často píše následovně.
![]() TBP = kbm
TBP = kbm
Zde ![]() TBP představuje zvýšení bodu varu – změna bodu varu, ke které dojde, když se rozpuštěná látka rozpustí v rozpouštědle
TBP představuje zvýšení bodu varu – změna bodu varu, ke které dojde, když se rozpuštěná látka rozpustí v rozpouštědle ![]() a kb je konstanta proporcionality známá jako molalová konstanta zvýšení bodu varu rozpouštědla.
a kb je konstanta proporcionality známá jako molalová konstanta zvýšení bodu varu rozpouštědla.
Podobnou rovnici lze napsat k popisu toho, co se stane s bodem mrazu (nebo teplotou tání) rozpouštědla, když se k rozpouštědlu přidá solute.
![]() TFP = -kfm
TFP = -kfm
V této rovnici je ![]() TFP bod mrazu deprese
TFP bod mrazu deprese ![]() změna bodu tuhnutí, která nastává, když se rozpustí rozpuštěná látka v rozpouštědle – a kfis je molová konstanta deprese bodu mrazu pro rozpouštědlo. V této rovnici se používá záporné znaménko k indikaci, že bod tuhnutí rozpouštědla klesá, když je přidána rozpuštěná látka.
změna bodu tuhnutí, která nastává, když se rozpustí rozpuštěná látka v rozpouštědle – a kfis je molová konstanta deprese bodu mrazu pro rozpouštědlo. V této rovnici se používá záporné znaménko k indikaci, že bod tuhnutí rozpouštědla klesá, když je přidána rozpuštěná látka.
Hodnoty kf a kbas, jakož i body tuhnutí a teploty varu pro řadu čistých rozpouštědel jsou uvedeny v tabulkách níže.
Konstanty deprese bodu mrazu
Konstanty zvýšení bodu varu
Praktický problém 6:
Vypočítejte molekulovou hmotnost síry, pokud se 35,5 gramů síry rozpustí ve 100,0 gramech CS2 za vzniku roztoku s bodem varu 49,48 ° C.
Kliknutím sem zkontrolujete odpověď na cvičný problém 6
Kliknutím sem zobrazíte řešení cvičného problému 6
Cvičení Problém 7:
Určete molekulovou hmotnost kyseliny octové, pokud roztok, který obsahuje 30,0 gramů kyseliny octové na kilogram vody zamrzne při -0,93 ° C. Souhlasí tyto výsledky s předpokladem, že kyselina octová má vzorec CH3CO2H?
Kliknutím sem zkontrolujete svoji odpověď na cvičný problém 7
Kliknutím sem zobrazíte řešení cvičného problému 7
Co by se stalo ve výpočtu v Praktickém problému 7 se opakovalo se silnější kyselinou, jako je kyselina chlorovodíková?
Cvičení Problém 8:
Vysvětlete, proč 0,100 m roztok HCl rozpuštěný v benzenu má pokles bodu tuhnutí 0,512 ° C, zatímco 0,100 m roztok HCl ve vodě má pokles bodu tuhnutí 0,352 ° C.
Kliknutím sem zkontrolujete odpověď na cvičný problém 8
V roce 1884 Jacobus Henricus van Hoff představil další zakončení deprese bodu mrazu a výšky bodu varu, aby vysvětlil koligativní vlastnosti roztoků sloučenin, které se disociují, když se rozpustí ve vodě.
![]() TFP = – kf (i) m
TFP = – kf (i) m
Dosazením experimentální hodnoty pro pokles bodu tuhnutí roztoku HCl 0,100 m do této rovnice se získá hodnota pro i i hodnotu 1,89. Pokud by se HCl neoddělil ve vodě, byl bych 1. Pokud by disocioval úplně, byl bych 2. Experimentální hodnota 1,89 navrhuje, aby se v tomto řešení disociovalo alespoň 95% molekul HCl.
Procvičování Problém 9:
Vysvětlete, proč se 0,60 gramu kyseliny octové rozpouští ve 200 gramech benzenu za vzniku roztoku, který snižuje bod tuhnutí benzenu na 5,40 ° C.
Kliknutím sem zkontrolujete svoji odpověď na Cvičení Problém 9
![]()
Osmotický tlak
V roce 1784 francouzský fyzik a kněz Jean AntoineNollet objevil, že se prasatový močový měchýř naplněný koncentrovaným roztokem alkoholu ve vodě rozšířil, když byl ponořen do vody. Močový měchýř fungoval jako semipermeabilní membrána, která umožňovala molekulám vody vstoupit do roztoku, ale bránila molekulám alkoholu v pohybu opačným směrem. Pohyb jedné složky roztoku přes membránu za účelem zředění roztoku se nazývá osmóza a tlak, který se vytváří, se nazývá osmotický tlak ().
Osmotický tlak lze demonstrovat pomocí přístroje zobrazeného na obrázku níže. Semipermeabilní membrána je vázána přes otevřený konec bodlák trubice. Trubice se poté částečně naplní roztokem cukru nebo alkoholu ve vodě a ponoří se do spodní části vody. Voda bude proudit do trubice, dokud tlak na sloupci vody v důsledku gravitační síly nevyrovná theosmotický tlak pohánějící vodu přes membránu.

Voda protéká semipermeabilní membrána k zředění alkoholového roztoku, dokud gravitační síla táhnoucí dolů na kolonu tohoto roztoku nevyvažuje osmotický tlak tlačící vodu přes membránu.
Ve stejném roce, kdy Raoult objevil vztah mezi tlakem par roztoku a tlakem par čisticího rozpouštědla, Jacobus Henricus van „t Hoff zjistil, že osmotický tlak zředěného roztoku () se řídí rovnicí analogickou k rovnici ideálního plynu.
| |
= | nRT | ||
| V |
Tato rovnice naznačuje, že osmotický tlak je dalším příkladem koligativní vlastnosti, protože toto závislost tlaku na poměru počtu částic rozpuštěné látky k objemu roztoku ![]() n / V
n / V ![]() ne na identitu částice rozpuštěné látky. také nám připomíná velikost osmotického tlaku. Podle této rovnice je 1,00 M s olutionh má osmotický tlak 22,4 atm při 0 ° C.
ne na identitu částice rozpuštěné látky. také nám připomíná velikost osmotického tlaku. Podle této rovnice je 1,00 M s olutionh má osmotický tlak 22,4 atm při 0 ° C.

To znamená, že 1,00 M řešení by mělo být schopné podporovat sloupec vody vysoký 670 palců nebo téměř 56 stop vysoký !
Biologové a biochemici často využívají osmotický tlak, když izolují složky buňky. Když je buňka přidána do vodného roztoku, který obsahuje mnohem vyšší koncentraci iontů než kapalina v buňce, voda opustí buňku protékáním buněčnou membránou, dokud se buňka nezmenší natolik, že se membrána rozbije. Alternativně, když je buňka umístěna do roztoku, který má mnohem menší iontovou sílu, nalije se do buňky voda a buňka se rozpíná, dokud nepraskne buněčná membrána.
![]()