Strmost kopce se nazývá sklon. Totéž platí pro strmost čáry. Sklon je definován jako poměr vertikální změny mezi dvěma body, vzestupu, k horizontální změně mezi stejnými dvěma body, běhu.

$$ sklon = \ frac {rise} {běh} = \ frac {change \: in \: y} {change \: in \: x} $$

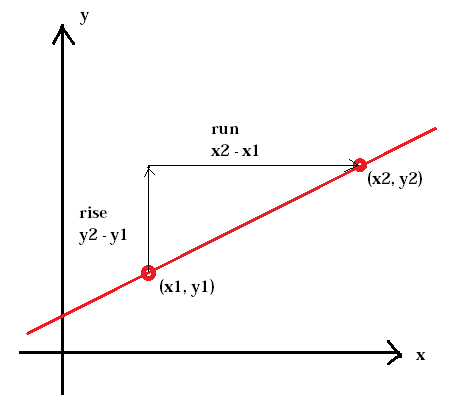
sklon přímky je obvykle reprezentován písmenem m. (x1, y1) představuje první bod, zatímco (x2, y2) představuje druhý bod.

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2 } \, -x_ {1}} $$

Je důležité zachovat souřadnice xay ve stejném pořadí jak v čitateli, tak ve jmenovateli, jinak získáte špatný sklon.

Příklad

Najděte sklon čáry

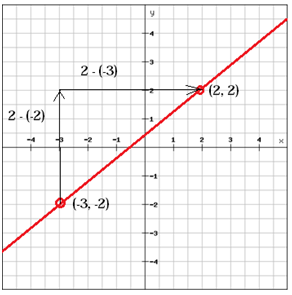
(x1, y1 ) = (-3, -2) a (x2, y2) = (2, 2)

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ { 2} \, -x_ {1}} = \ frac {2- \ levý (-2 \ pravý)} {2- \ levý (-3 \ pravý)} = \ frac {2 + 2} {2 + 3} = \ frac {4} {5} $$

Řádek s kladným sklonem (m > 0), jako řádek výše, stoupá zleva zatímco čára se záporným sklonem (m < 0) klesá zleva doprava.

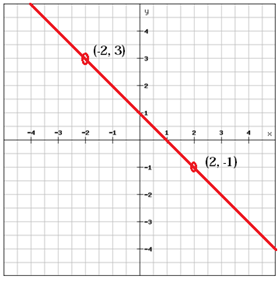
$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2} \, -x_ {1}} = \ frac {\ vlevo (-1 \ vpravo) -3} {2- \ left (-2 \ right)} = \ frac {-1-3} {2 + 2} = \ frac {-4} {4} = – 1 $$

Pokud mají dvě čáry stejný sklon, říká se, že čáry jsou str souběžně.

Lineární funkci můžete vyjádřit pomocí formuláře pro zachycení sklonu.

$$ y = mx + b $$

$$ m = sklon $ $

$$ b = y – zachytit $$

Video lekce

Najít sklon