Výpočty síly

Síla je push nebo pull.
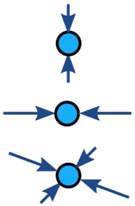
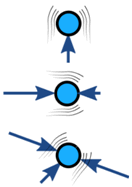
Síly na objekt jsou obvykle vyvážené (pokud je nevyvážené, objekt se zrychluje):
 |
 |
|
| Vyvážený | Nevyvážený | |
|---|---|---|
| Žádná akcelerace | Zrychlení |
Příklad: Síly v horní části této mostní věže jsou vyvážené (nezrychluje se):

Kabely se táhnou směrem dolů rovnoměrně doleva a doprava, což je vyváženo tlakem věže nahoru. (Tlačí věž? Ano! Představte si, že tam stojíte místo věže.)
Sily můžeme modelovat takto:

A když postavíme-li je od hlavy k patě, vidíme, že se uzavírají zpět, což znamená, že čistý efekt je nulový:

Síly jsou v rovnováze.
Síly v rovnováze jsou považovány za rovnovážné: nedochází ani ke změnám v pohybu.
Diagramy volného těla
Prvním krokem je k nakreslení diagramu volného těla (také nazývaného silový diagram)
Diagram volného těla: Skica, kde je tělo vyříznuto ze světa kromě sil působících na něj.
V příkladu mostu je schéma volného těla pro horní část věže:

Diagram volného těla
Pomáhá musíme jasně přemýšlet o silách působících na tělo.
Příklad: Auto na dálnici
Jaké jsou síly na auto křižující po dálnici?

Motor pracuje tvrdě, tak proč auto nezrychluje?
Protože jízda síla je vyvážena:
- odpor vzduchu (jednoduše řečeno: th Vzduch vzdoruje tlačení),
- Valivý odpor, nazývaný také valivé tření (pneumatiky odolávají změnám tvaru)

Schéma volné karoserie
W je hmotnost vozu,
R1 a R2 jsou valivý odpor pneumatik,
N1 a N2 jsou reakční síly (vyvažující hmotnost vozu).
Poznámka: ocelová kola (jako u vlaků) mají menší valivý odpor, ale na silnici jsou příliš kluzká!
Výpočty
Síla je vektor. Vektor má velikost (velikost) a směr:

Sily můžeme modelovat nakreslením šipek správné velikosti a směru . Například:
Příklad: Obdivování pohledu
Brady stojí na okraji balkónu, který je podepřen vodorovným nosníkem a podpěrou:

Váží 80 kg.
Jaké jsou síly?
Pojďme si vzít místo, na kterém stojí, a přemýšlet o silách, které tam jsou:

Jeho váha
Jeho hmotnost 80 kg vytváří sílu dolů díky gravitaci.
Síla je hmotnost krát zrychlení: F = ma
Zrychlení gravitací na Zemi je 9,81 m / s2 , takže a = 9,81 m / s2
F = 80 kg × 9,81 m / s2
F = 785 N
Ostatní síly
Síly jsou vyvážené, takže by se měly samy uzavřít takto:

K vyřešení můžeme použít trigonometrii .
Protože se jedná o pravoúhlý trojúhelník, SOHCAHTOA pomůže.
U paprsku známe sousední, chceme znát protiklad a „TOA“ nám říká, abychom použili tangens:
opálení (60 ° ) = Paprsek / 785 N
paprsek / 785 N = opálení (60 °)
paprsek = opálení (60 °) × 785 N
paprsek = 1,732 … × 785 N = 1360 N
U Strut známe sousední, chceme znát hypotenzi a „CAH“ nám říká, abychom použili kosinus:
cos (60 °) = 785 N / podpěra
Strut × cos (60 °) = 785 N
Strut = 785 N / cos (60 °)
Strut = 785 N / 0,5 = 1570 N
Vyřešeno:

Zajímavé, na kolik síly působí paprsek a vzpěra ve srovnání s podporovanou hmotností!
Točivý moment (nebo moment)
Co když je paprsek právě zaseknutý ve zdi (nazývá se konzola)?

Neexistuje žádná podpěra, tak co se stane se silami?
Diagram volného těla vypadá takto:

Síla nahoru R vyvažuje váhu směrem dolů.
Pouze s těmito dvěma nutí paprsek se točit jako vrtule! Ale existuje také „efekt otáčení“ M zvaný Moment (nebo Torque), který to vyvažuje:
Moment: Síla krát Vzdálenost v pravém úhlu.
Víme, že Weight is 785 N, a také potřebujeme znát vzdálenost v pravých úhlech, která je v tomto případě 3,2 m.
M = 785 N x 3,2 m = 2512 Nm
A ten okamžik je to, co zastaví paprsek v otáčení.

Když držíte rybářský prut, můžete cítit okamžik.
Kromě toho, že držíte svou váhu, musíte zabránit jejímu otáčení směrem dolů.
Tření
Box na rampě
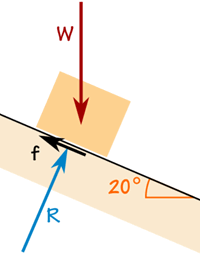
Krabice váží 100 kg.
Třecí síla stačí k tomu, aby zůstala tam, kde je.
Reakční síla R je kolmá k rampa.
Box se nezrychluje, takže síly jsou v rovnováze:
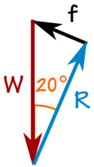
100 kg hmotnosti vytváří sílu dolů díky gravitaci:
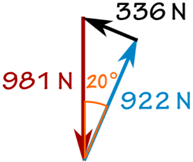
W = 100 kg × 9,81 m / s2 = 981 N
K vyřešení trojúhelníku můžeme použít SOHCAHTOA.
Tření f:
sin (20 °) = f / 981 N
f = sin (20 °) × 981 N = 336 N
Reakce N:
cos (20 °) = R / 981 N
R = cos (20 °) × 981 N = 922 N
A dostaneme:
Tipy pro kreslení diagramů těla zdarma
- Kreslete co nejjednodušším způsobem. Krabice je často dost dobrá.
- Síly ukazují ve směru, kterým působí na tělo
- přímé šipky pro síly
- zakřivené šipky na okamžiky
Sam a Alex vytáhnou krabici
Výpočty mohou být někdy snazší, když velikost a směr změníme na x a y:
 |
< = > |  |
| Vektor v polárních souřadnicích |
Vektor a v kartézských souřadnicích |
Jak je převést si můžete přečíst v Polárních a kartézských Souřadnice, ale zde je stručné shrnutí:
Pojďme je použít!