Parametrické a neparametrické testy pro porovnání dvou nebo více skupin

Statistiky: Parametrické a neparametrické testy

Tato část zahrnuje:

• Výběr testu
• Parametrické testy
• Neparametrické testy

Výběr testu

Z hlediska výběru statistického testu je nejdůležitější otázkou „jaká je hlavní studijní hypotéza?“ V některých případech neexistuje hypotéza; vyšetřovatel chce jen „zjistit, co tam je“. Například ve studii prevalence neexistuje žádná hypotéza k testování a velikost studie je určena tím, jak přesně chce vyšetřovatel prevalenci určit. Pokud neexistuje hypotéza, neexistuje statistický test. Je důležité a priori rozhodnout, které hypotézy jsou potvrzující (tj. Testují nějaký předpokládaný vztah) a které jsou průzkumné (naznačují data). Žádná jednotlivá studie nemůže podpořit celou řadu hypotéz. Rozumným plánem je přísně omezit počet potvrzujících hypotéz. Ačkoli je platné používat statistické testy na hypotézách navrhovaných údaji, hodnoty P by měly být použity pouze jako vodítko a výsledky by měly být považovány za předběžné, dokud nebudou potvrzeny dalšími studiemi. Užitečným průvodcem je použití Bonferroniho korekce, která jednoduše říká, že pokud testujete n nezávislých hypotéz, měli byste použít hladinu významnosti 0,05 / n. Pokud by tedy existovaly dvě nezávislé hypotézy, byl by výsledek prohlášen za významný pouze v případě, že P < 0,025. Vzhledem k tomu, že testy jsou zřídka nezávislé, jedná se o velmi konzervativní postup – tj. Je nepravděpodobné, že by nulovou hypotézu odmítl. Vyšetřovatel by se měl poté zeptat „jsou údaje nezávislé?“ To může být obtížné rozhodnout, ale zpravidla nejsou výsledky u stejného jedince nebo od spárovaných jedinců nezávislé. Výsledky křížového pokusu nebo studie případové kontroly, ve které byly kontroly přizpůsobeny případům podle věku, pohlaví a sociální třídy, tedy nejsou nezávislé.

• Analýza by měla odrážet design , a proto by po shodném designu měla následovat shodná analýza.
• Výsledky měřené v čase vyžadují zvláštní péči. Jednou z nejčastějších chyb ve statistické analýze je zacházet s korelovanými proměnnými, jako by byly nezávislé
  nezávislé. Předpokládejme například, že jsme sledovali léčbu bércových vředů, při nichž někteří lidé měli vředy na nohou. Mohli bychom mít 20 subjektů s 30 vředy, ale počet nezávislých informací je 20, protože stav vředů na každé noze u jedné osoby může být ovlivněn zdravotním stavem osoby a analýzou, která považoval vředy za nezávislé pozorování by bylo nesprávné. Pro správnou analýzu smíšených spárovaných a nepárových
  dat se obraťte na statistika.

Další otázka je „jaké typy dat se měří?“ Použitý test by měl být určen podle údajů. Volba testu pro spárovaná nebo spárovaná data je popsána v tabulce 1 a pro nezávislá data v tabulce 2.

Tabulka 1 Výběr statistického testu ze spárovaného nebo spárovaného pozorování

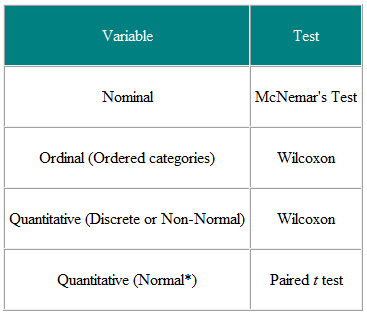
Je užitečné rozhodovat o vstupních proměnných a výsledných proměnných. Například v klinické studii je vstupní proměnnou typ léčby – nominální proměnná – a výsledkem může být nějaká klinická míra, možná normálně distribuovaná. Požadovaným testem je pak t-test (tabulka 2). Pokud je však vstupní proměnná spojitá, řekněme klinické skóre, a výsledek je nominální, řekněme vyléčená nebo nevyléčená, je požadovanou analýzou logistická regrese. T-test v tomto případě může pomoci, ale nedal by nám to, co požadujeme, konkrétně pravděpodobnost vyléčení dané hodnoty klinického skóre. Jako další příklad předpokládejme, že máme průřezovou studii, ve které se ptáme náhodného vzorku lidí, zda si myslí, že jejich praktický lékař dělá dobrou práci, na pětibodové stupnici, a rádi bychom zjistili, zda mají ženy vyšší mínění praktických lékařů než muži. Vstupní proměnnou je pohlaví, které je nominální. Výsledná proměnná je pětibodová řadová stupnice. Názor každého člověka je nezávislý na ostatních, takže máme nezávislá data. Z tabulky 2 bychom měli použít test χ2 pro trend, nebo Mann-Whitney U test s korekcí na vazby (poznámka: hodnoty jsou stejné, takže neexistuje striktně rostoucí pořadí pořadí – tam, kde k tomu dojde, lze průměrovat pořadí pro vázané hodnoty). Všimněte si však, že pokud někteří lidé sdílejí praktického lékaře a jiní ne, pak údaje nejsou nezávislá a vyžaduje se sofistikovanější analýza. Upozorňujeme, že tyto tabulky by měly být považovány pouze za vodítka a každý případ by měl být posuzován podle jeho podstaty.

Tabulka 2 Volba statistického testu pro nezávislá pozorování

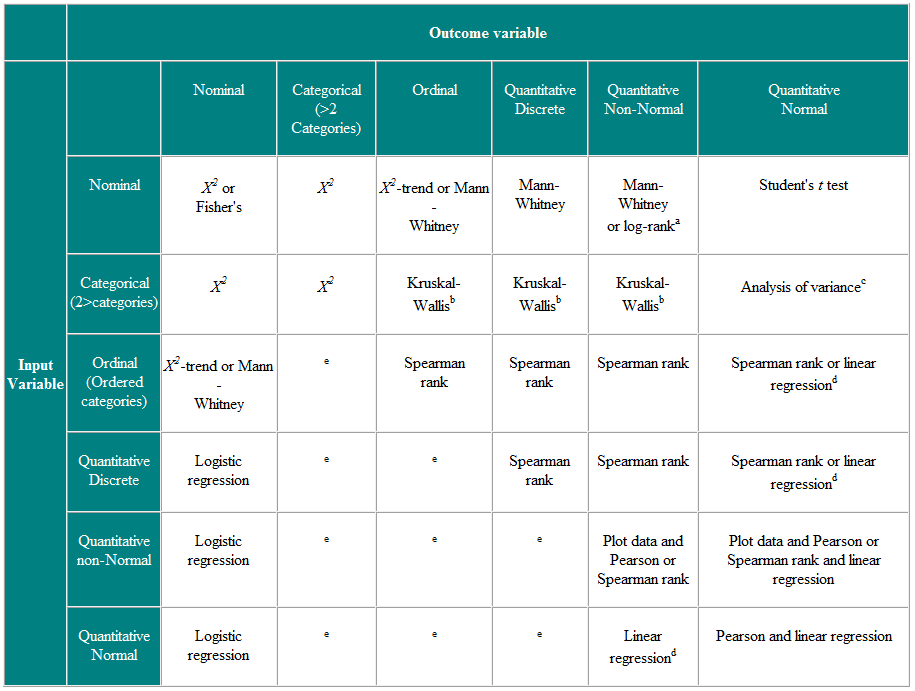
a Pokud jsou data cenzurována. b Kruskal-Wallisův test se používá k porovnání řadových nebo nenormálních proměnných pro více než dvě skupiny a je zobecněním Mann-Whitneyho U testu. c Analýza rozptylu je obecná technika a jedna verze (jednosměrná analýza rozptylu) se používá k porovnání normálně distribuovaných proměnných pro více než dvě skupiny a je parametrickým ekvivalentem Kruskal-Wallistest. d Pokud je výsledná proměnná závislá proměnná, pak za předpokladu, že rezidua (rozdíly mezi pozorovanými hodnotami a predikovanými odpověďmi z regrese) jsou věrohodně normálně distribuovány, pak distribuce nezávislé proměnné není důležitá. e Existuje řada pokročilejších technik, jako je Poissonova regrese, pro řešení těchto situací. Vyžadují však určité předpoklady a je často snazší buď dichotomizovat výslednou proměnnou, nebo ji považovat za spojitou.

Parametrické testy jsou ty, které vytvářejí předpoklady o parametrech distribuce populace, ze které je vzorek čerpán . Často se jedná o předpoklad, že údaje o populaci jsou normálně distribuovány. Neparametrické testy jsou „bez distribuce“ a jako takové je lze použít pro jiné než normální proměnné. Tabulka 3 ukazuje neparametrický ekvivalent řady parametrických testů.

Tabulka 3 Parametrické a Neparametrické testy pro porovnání dvou nebo více skupin

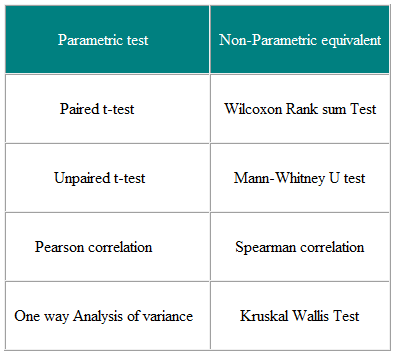
Neparametrické testy jsou platné pro data, která nejsou normálně distribuována, a Normálně distribuovaná data, tak proč je nepoužívat pořád?

Zdá se být rozumné používat neparametrické testy ve všech případech, což by ušetřilo obtěžování z testování Normality. Preferovány jsou parametrické testy, ale z následujících důvodů:

1. Zřídka nás zajímá pouze test významnosti; rádi bychom řekli něco o populaci, ze které vzorky pocházejí, a to se nejlépe provádí pomocí
odhady parametrů a intervaly spolehlivosti.

2. Je obtížné provést flexibilní modelování pomocí neparametrických testů, například umožnit matoucí faktory pomocí více regrese.

3. Parametrické testy mají obvykle větší statistickou sílu než jejich neparametrické ekvivalenty. Jinými slovy, je pravděpodobnější, že zjistíme významné rozdíly, když
skutečně existují.

Porovnávají neparametrické testy medián?

Běžně se věří, že Mann-Whitneyův U test je ve skutečnosti testem rozdílů v mediánu. Dvě skupiny však mohly mít stejný medián a přesto mít významný Mann-Whitneyův U test. Zvažte následující data pro dvě skupiny, každá se 100 pozorováními. Skupina 1: 98 (0), 1, 2; Skupina 2: 51 (0), 1, 48 (2). Medián v obou případech je 0, ale z Mann-Whitneyova testu P < 0,0001. Pouze pokud jsme připraveni učinit další předpoklad, že rozdílem v obou skupinách je pouze posun v místě (tj. Distribuce dat v jedné skupině se jednoduše posune o pevnou částku od druhé), můžeme říci, že test je testem rozdílu v mediánu. Pokud však skupiny mají stejné rozdělení, pak posun v umístění posune mediány a prostředky o stejnou částku, takže rozdíl v mediánech je stejný jako rozdíl v prostředcích. Mann-Whitneyův U test je tedy také testem rozdílu průměrů. Jak souvisí test Mann-Whitney U s t-testem? Pokud bychom měli do programu t-test se dvěma vzorky zadat spíše data než samotná data, byla by získaná hodnota P velmi blízká hodnotě produkované Mann-Whitneyovým U testem.