Stejlheden på en bakke kaldes en hældning. Det samme gælder stejlheden i en linje. Hældningen er defineret som forholdet mellem den lodrette ændring mellem to punkter, stigningen, og den vandrette ændring mellem de samme to punkter, løbet.

$$ hældning = \ frac {rise} {run} = \ frac {ændring \: i \: y} {ændring \: i \: x} $$

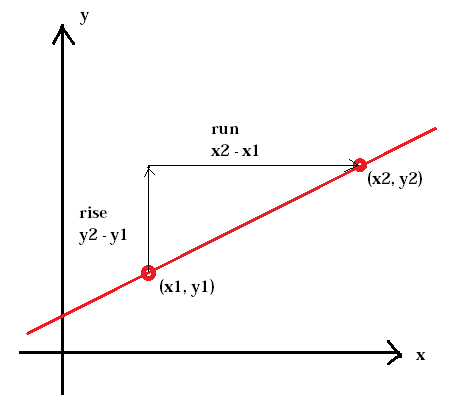
hældning af en linje er normalt repræsenteret af bogstavet m. (x1, y1) repræsenterer det første punkt, mens (x2, y2) repræsenterer det andet punkt.

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2 } \, -x_ {1}} $$

Det er vigtigt at holde x- og y-koordinaterne i samme rækkefølge i både tælleren og nævneren ellers får du den forkerte hældning.

Eksempel

Find linjens hældning

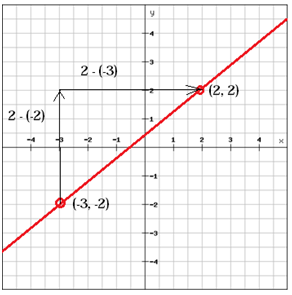
(x1, y1 ) = (-3, -2) og (x2, y2) = (2, 2)

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ { 2} \, -x_ {1}} = \ frac {2- \ venstre (-2 \ højre)} {2- \ venstre (-3 \ højre)} = \ frac {2 + 2} {2 + 3} = \ frac {4} {5} $$

En linje med en positiv hældning (m > 0), som linien ovenfor, stiger fra venstre til til højre, mens en linje med negativ hældning (m < 0) falder fra venstre mod højre.

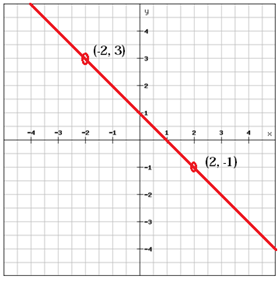
$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2} \, -x_ {1}} = \ frac {\ left (-1 \ right) -3} {2- \ left (-2 \ right)} = \ frac {-1-3} {2 + 2} = \ frac {-4} {4} = – 1 $$

Hvis to linjer har samme hældning, siges linjerne at være p arallel.

Du kan udtrykke en lineær funktion ved hjælp af hældningsafskæringsformularen.

$$ y = mx + b $$

$$ m = hældning $ $

$$ b = y – opfange $$

Videolektion

Find hældningen