• K-tætteste nabo er en af de mest enkle maskinlæringsalgoritmer baseret om Supervised Learning-teknik.
• K-NN-algoritmen antager ligheden mellem den nye sag / data og tilgængelige sager og placerer den nye sag i den kategori, der mest ligner de tilgængelige kategorier.
• K-NN algoritme gemmer alle tilgængelige data og klassificerer et nyt datapunkt baseret på ligheden. Det betyder, at når nye data vises, kan de let klassificeres i en brøndpakke-kategori ved hjælp af K-NN-algoritme.
• K-NN-algoritme kan bruges til regression såvel som til klassificering, men for det meste bruges den til klassificeringsproblemerne.
• K-NN er en ikke-parametrisk algoritme, hvilket betyder det antager ingen antagelser om underliggende data.
• Det kaldes også en doven elevalgoritme, fordi den ikke lærer af træningssættet med det samme i stedet for at gemme datasættet og på klassifikationstidspunktet udfører det en handling på datasættet.
• KNN-algoritme i træningsfasen gemmer bare datasættet, og når det får nye data, klassificerer det disse data i en kategori, der meget ligner de nye data.
• Eksempel: Antag, vi har et billede af et væsen, der ligner kat og hund, men vi vil gerne vide, om det er en kat eller hund. Så til denne identifikation kan vi bruge KNN-algoritmen, da den fungerer på et lighedsmål. Vores KNN-model finder de samme funktioner i det nye datasæt til katte- og hundebillederne og baseret på de mest lignende funktioner vil den placere den i enten kat- eller hundekategori.

Hvorfor har vi brug for en K-NN algoritme?

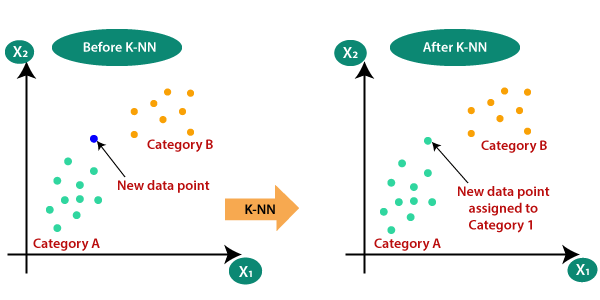
Antag at der er to kategorier, dvs. kategori A og kategori B, og vi har et nyt datapunkt x1, så dette datapunkt ligger i hvilken af disse kategorier. For at løse denne type problemer har vi brug for en K-NN-algoritme. Ved hjælp af K-NN kan vi let identificere kategorien eller klassen for et bestemt datasæt. Overvej nedenstående diagram:

Hvordan fungerer K-NN?

K-NN-arbejdet kan forklares på baggrund af nedenstående algoritme:

• Trin-1: Vælg antallet K for naboerne
• Trin-2: Beregn den euklidiske afstand for K antallet af naboer
• Trin 3: Tag K nærmeste naboer i henhold til den beregnede euklidiske afstand.
• Trin 4: Bland disse k naboer, tæl antallet af datapunkter i hver kategori.
• Trin 5: Tildel de nye datapunkter til den kategori, hvor naboens antal er maksimalt.
• Trin-6: Vores model er klar.

Antag, at vi har et nyt datapunkt, og vi skal sætte det i den krævede kategori. Overvej nedenstående billede:

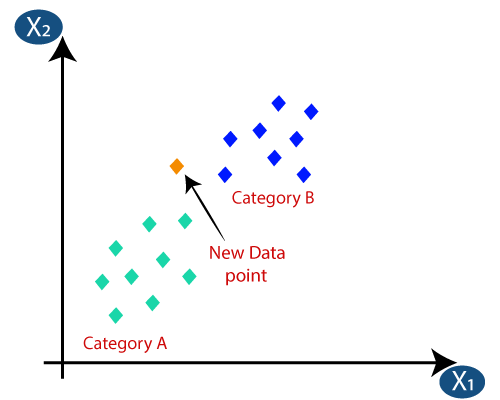
• For det første vælger vi antallet af naboer, så vi vælger k = 5.
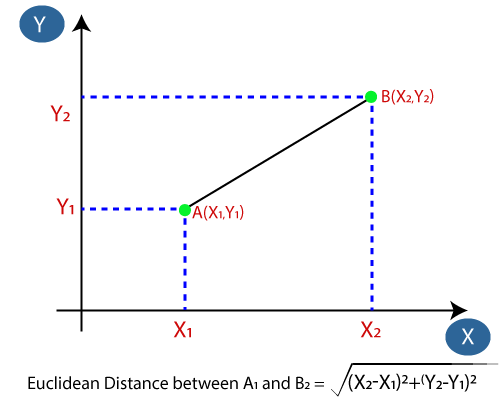
• Dernæst beregner vi den euklidiske afstand mellem datapunkterne. Den euklidiske afstand er afstanden mellem to punkter, som vi allerede har studeret i geometri. Det kan beregnes som:

• Ved at beregne den euklidiske afstand fik vi de nærmeste naboer som tre nærmeste naboer i kategori A og to nærmeste naboer i kategori B. Overvej nedenstående billede:

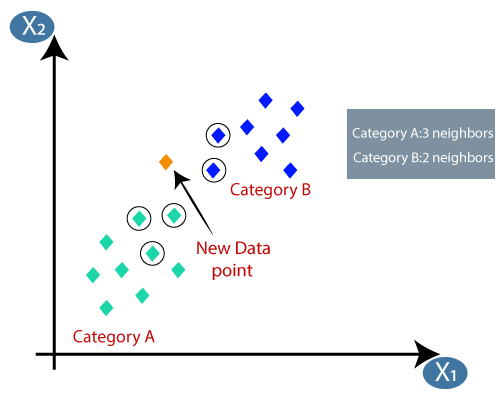
• Som vi kan se, er de 3 nærmeste naboer fra kategori A, derfor skal dette nye datapunkt tilhøre kategori A.

Hvordan vælges værdien af K i K-NN-algoritmen?

Nedenfor er nogle punkter til husk, mens du valgte værdien af K i K-NN-algoritmen:

• Der er ingen særlig måde at bestemme den bedste værdi for “K”, så vi er nødt til at prøve nogle værdier for at finde de bedste ud af dem. Den mest foretrukne værdi for K er 5.
• En meget lav værdi for K, såsom K = 1 eller K = 2, kan være støjende og føre til virkningerne af outliers i modellen.
• Store værdier for K er gode, men det kan finde nogle vanskeligheder.

Fordele ved KNN-algoritme:

• Det er simpelt at implementere.
• Det er robust over for de støjende træningsdata
• Det kan være mere effektivt, hvis træningsdataene er store.

Ulemper ved KNN-algoritme:

• Har altid brug for at bestemme værdien af K, som kan være kompleks i nogen tid.
• Beregningsomkostningerne er høje på grund af beregningen af afstanden mellem datapunkterne for alle træningseksemplerne .

Python-implementering af KNN-algoritmen

For at udføre Python-implementeringen af K-NN-algoritmen bruger vi det samme problem og datasæt, som vi har brugt i Logistisk regression. Men her vil vi forbedre modelens ydeevne. Nedenfor er problembeskrivelsen:

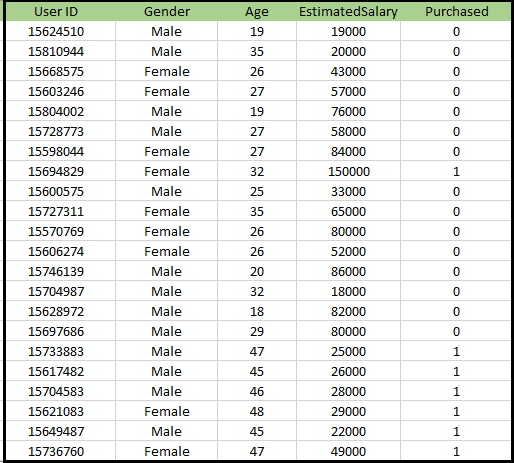
Problem for K-NN algoritme: Der er et bilproducentfirma, der har produceret en ny SUV-bil.Virksomheden ønsker at give annoncerne til de brugere, der er interesserede i at købe den SUV. Så for dette problem har vi et datasæt, der indeholder flere brugeroplysninger gennem det sociale netværk. Datasættet indeholder masser af information, men den estimerede løn og alder, vi vil overveje for den uafhængige variabel, og den købte variabel er for den afhængige variabel. Nedenfor er datasættet:

Trin til implementering af K-NN-algoritmen:

• Dataforbehandlingstrin
• Tilpasning af K-NN-algoritmen til træningssættet
• Forudsigelse af testresultatet
• Testnøjagtighed af resultatet (Oprettelse af forvirringsmatrix)
• Visualisering af testsættets resultat.

Trin til forbehandling af data:

Dataforbehandlingstrinnet forbliver nøjagtigt det samme som logistisk regression. Nedenfor er koden for det:

Ved at udføre ovenstående kode importeres vores datasæt til vores program og forbehandles godt. Efter funktionsskalering vil vores testdatasæt se ud som:

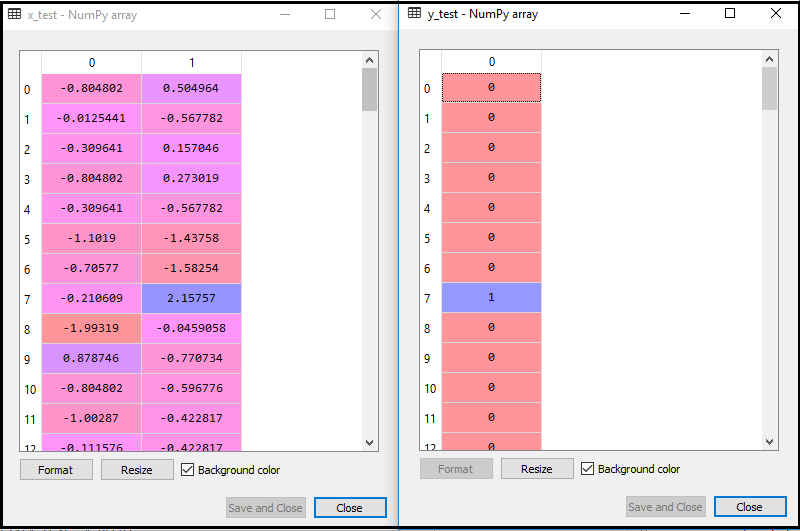
Fra ovenstående output im alder, kan vi se, at vores data er vellykket skaleret.

• Tilpasning af K-NN-klassifikator til træningsdataene:
  Nu passer vi K-NN-klassifikatoren til træningsdataene. For at gøre dette importerer vi KNeighborsClassifier-klassen i Sklearn Neighbors-biblioteket. Efter import af klassen opretter vi klassifikationsobjektet for klassen. Parameteren for denne klasse vil være
  • n_nebors: At definere de krævede naboer til algoritmen. Normalt tager det 5.
  • metric = “minkowski”: Dette er standardparameteren, og det bestemmer afstanden mellem punkterne.
  • p = 2: Det svarer til standarden Euklidisk metric.

  Og så passer vi klassifikatoren til træningsdataene. Nedenfor er koden til det:

Output: Ved at udføre ovenstående kode får vi output som:

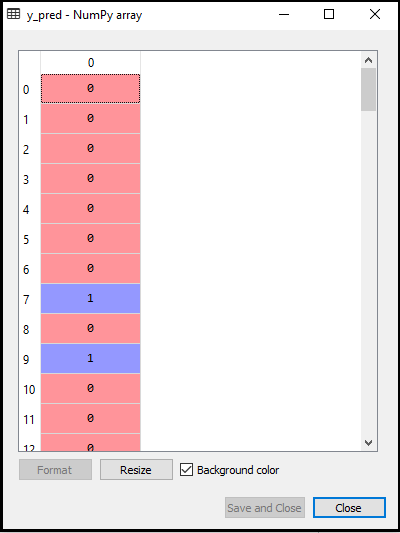
• Forudsigelse af testresultatet: For at forudsige testsættets resultat opretter vi en y_pred-vektor som vi gjorde i Logistisk regression. Nedenfor er koden til det:

Output:

Outputtet for ovenstående kode vil være:

• Oprettelse af forvirringsmatrix:
  Nu opretter vi forvirringsmatrix til vores K-NN-model for at se nøjagtigheden af klassificeringen. Nedenfor er koden til det:

I ovenstående kode har vi importeret confusion_matrix-funktionen og kaldt den ved hjælp af variablen cm.

Output: Ved at udføre ovenstående kode får vi matrixen som nedenfor:

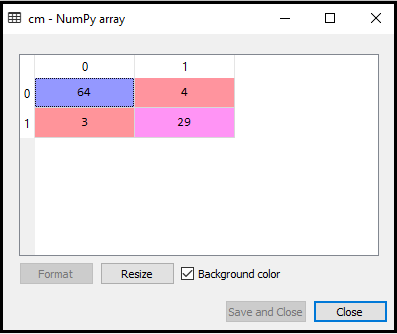
I ovenstående billede kan vi se der er 64 + 29 = 93 korrekte forudsigelser og 3 + 4 = 7 forkerte forudsigelser, mens der i Logistisk regression var 11 forkerte forudsigelser. Så vi kan sige, at ydeevnen af modellen forbedres ved hjælp af K-NN-algoritmen.

• Visualisering af træningssætresultatet:
  Nu vil vi visualisere træningssætresultatet for K -NN-model. Koden forbliver den samme som vi gjorde i Logistisk regression, undtagen navnet på grafen. Nedenfor er koden til det:

Output:

Ved at udføre ovenstående kode får vi nedenstående graf:

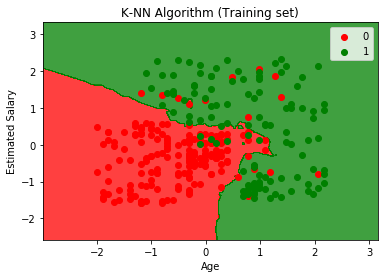
Outputgrafen er forskellig fra den graf, som vi har fundet sted i Logistisk regression. Det kan forstås i nedenstående punkter:

• Som vi kan se, viser grafen det røde punkt og de grønne punkter. De grønne punkter er for købt (1) og røde punkter for ikke købt (0) variabel.
• Grafen viser en uregelmæssig grænse i stedet for at vise en lige linje eller en hvilken som helst kurve, fordi det er en K-NN-algoritme, dvs. at finde den nærmeste nabo.
• Grafen har klassificeret brugere i de rigtige kategorier, da de fleste brugere, der ikke købte SUV’erne, er i den røde region, og brugere, der har købt SUV’en, er i den grønne region.
• Grafen viser et godt resultat, men der er stadig nogle grønne punkter i den røde region og røde punkter i den grønne region. Men dette er ikke noget stort problem, da man ved at gøre denne model forhindres i at overmontere problemer.
• Derfor er vores model veluddannet.
• Visualisering af testsættets resultat:
  Efter træning af modellen vil vi nu teste resultatet ved at sætte et nyt datasæt, dvs. Testdatasæt. Koden forbliver den samme undtagen nogle mindre ændringer: såsom x_train og y_train erstattes af x_test og y_test.
  Nedenfor er koden til det:

Output:

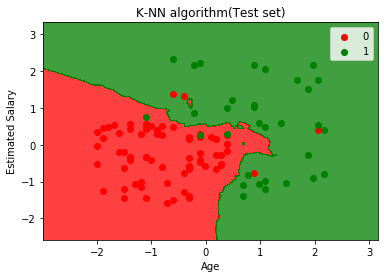
Ovenstående graf viser output for testdatasættet. Som vi kan se i grafen, er den forudsagte output godt godt, da de fleste af de røde punkter er i den røde region og de fleste af de grønne punkter er i den grønne region.

Der er dog få grønne punkter i den røde region og et par røde punkter i den grønne region. Så dette er de forkerte observationer, som vi har observeret i forvirringsmatrixen (7 Forkert output).