Kraftberegninger

Kraft er push eller pull.
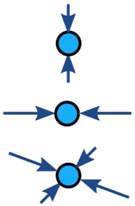
Styrker på et objekt er normalt afbalanceret (hvis det ikke er i balance, accelererer objektet):
 |
 |
|
| Balanceret | Ubalanceret | |
|---|---|---|
| Ingen acceleration | Acceleration |
Eksempel: Kræfterne øverst i dette brotårn er i balance (det accelererer ikke):

Kablerne trækkes lige ned til venstre og højre, og det er afbalanceret af tårnets skub opad (skubber tårnet? Ja! Forestil dig at du står der i stedet for tårnet.)
Vi kan modellere kræfterne sådan:

Og når vi sæt dem hoved-til-hale, vi ser, at de lukker sig tilbage, hvilket betyder, at nettoeffekten er nul:

Styrkerne er i balance.
Styrker i balance siges at være i ligevægt: der er heller ingen ændring i bevægelse.
Diagrammer med fri krop
Det første trin er at tegne et frit kropsdiagram (også kaldet et kraftdiagram)
Gratis kropsdiagram: en skitse, hvor et legeme er skåret fri fra verden bortset fra de kræfter, der virker på det.
I broeksemplet er det frie kropsdiagram til toppen af tårnet:

Gratis kropsdiagram
Det hjælper os til at tænke klart om de kræfter, der virker på kroppen.
Eksempel: Bil på en motorvej
Hvad er kræfterne på en bil, der kører ned ad motorvejen?

Motoren arbejder hårdt, så hvorfor fortsætter ikke bilen med at accelerere?
Fordi kørslen kraft afbalanceres af:
- Luftmodstand (enkelt sagt: th e luft modstår at blive skubbet rundt),
- Rullemodstand, også kaldet rullende friktion (dækkene modstår at have deres form ændret)

Free Body Diagram
W er bilens vægt,
R1 og R2 er dækkets rullemodstand,
N1 og N2 er reaktionskræfterne (afvejning af bilens vægt).
Bemærk: stålhjul (som i tog) har mindre rullemodstand, men er alt for glatte på vejen!
Beregninger
Force er en vektor. En vektor har størrelse (størrelse) og retning:

Vi kan modellere kræfterne ved at tegne pile med den rigtige størrelse og retning . Som dette:
Eksempel: Beundrer udsigten
Brady står på kanten af en altan understøttet af en vandret bjælke og en stiver:

Han vejer 80 kg.
Hvad er kræfterne?
Lad os tage den plads, han står på, og tænke på kræfterne lige der:

Hans vægt
Hans 80 kg masse skaber en nedadgående kraft på grund af tyngdekraften.
Kraft er masse gange acceleration: F = ma
Accelerationen på grund af tyngdekraften på jorden er 9,81 m / s2 , så a = 9,81 m / s2
F = 80 kg × 9,81 m / s2
F = 785 N
De øvrige styrker
Kræfterne er afbalancerede, så de bør lukke sig selv på denne måde:

Vi kan bruge trigonometri til at løse det .
Fordi det er en retvinklet trekant, vil SOHCAHTOA hjælpe.
For bjælken kender vi den tilstødende, vi vil kende det modsatte, og “TOA” fortæller os at bruge Tangent:
tan (60 ° ) = Stråle / 785 N
Stråle / 785 N = tan (60 °)
Stråle = tan (60 °) × 785 N
Stråle = 1.732 … × 785 N = 1360 N
For stammen kender vi det tilstødende, vi ønsker at kende hypotenusen, og “CAH” fortæller os at bruge Cosine:
cos (60 °) = 785 N / stiver
Stiv × cos (60 °) = 785 N
Stiv = 785 N / cos (60 °)
Strut = 785 N / 0.5 = 1570 N
Løst:

Interessant, hvor meget kraft der er på bjælken og stiverne sammenlignet med den vægt, der understøttes!
Moment (eller Moment)
Hvad hvis bjælken bare sidder fast i væggen (kaldet en cantilever)?

Der er ingen støttestiv, så hvad sker der med kræfterne?
Diagrammet for fri krop ser sådan ud:

Den opadgående kraft R afbalancerer vægten nedad.
Med kun de to styrker strålen vil dreje som en propel! Men der er også en “drejningseffekt” M kaldet Moment (eller Torque), der afbalancerer den:
Moment: Force gange afstanden vinkelret.
Vi ved, at vægten er 785 N, og vi skal også kende afstanden vinkelret, som i dette tilfælde er 3,2 m.
M = 785 N x 3,2 m = 2512 Nm
Og det øjeblik er det, der forhindrer strålen i at rotere.

Du kan føle et øjeblik, når du holder fast i en fiskestang.
Ud over at holde vægten op, skal du stoppe den fra at rotere nedad.
Friktion
Boks på en rampe
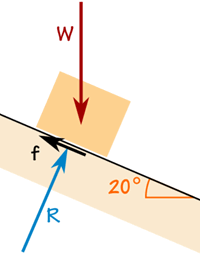
Kassen vejer 100 kg.
Friktionskraften er tilstrækkelig til at holde den, hvor den er.
Reaktionskraften R er vinkelret på rampe.
Boksen accelererer ikke, så kræfterne er i balance:
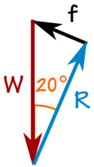
De 100 kg masse skaber en nedadgående kraft på grund af tyngdekraften:
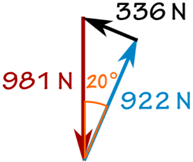
W = 100 kg × 9,81 m / s2 = 981 N
Vi kan bruge SOHCAHTOA til at løse trekanten.
Friktion f:
sin (20 °) = f / 981 N
f = sin (20 °) × 981 N = 336 N
Reaktion N:
cos (20 °) = R / 981 N
R = cos (20 °) × 981 N = 922 N
Og vi får:
Tip til at tegne gratis kropsdiagrammer
- Tegn så enkelt som muligt. En kasse er ofte god nok.
- Styrker peger i den retning, de virker på kroppen
- lige pile for kræfter
- buede pile i øjeblikke
Sam og Alex trækker en kasse
Beregningerne kan nogle gange være lettere, når vi vender størrelse og retning til x og y:
 |
< = > |  |
| Vector a i Polar koordinater |
Vector a i kartesisk koordinater |
Du kan læse, hvordan du konverterer dem på Polar og Cartesian Koordinater, men her er et hurtigt resume:
Lad os bruge dem!