Parametriske og ikke-parametriske tests til sammenligning af to eller flere grupper

Statistik: Parametriske og ikke-parametriske tests

Dette afsnit dækker:

• Valg af test
• Parametriske tests
• Ikke-parametriske tests

Valg af test

Med hensyn til valg af en statistisk test er det vigtigste spørgsmål “hvad er hovedundersøgelseshypotesen?” I nogle tilfælde er der ingen hypotese; efterforskeren vil bare “se, hvad der er der”. For eksempel er der i en prævalensundersøgelse ingen hypotese at teste, og undersøgelsens størrelse bestemmes af, hvor præcist efterforskeren vil bestemme prævalensen. Hvis der ikke er nogen hypotese, er der ingen statistisk test. Det er vigtigt at beslutte på forhånd, hvilke hypoteser der er bekræftende (det vil sige at teste noget formodet forhold), og hvilke der er udforskende (er foreslået af dataene). Ingen enkelt undersøgelse kan understøtte en hel række hypoteser. En fornuftig plan er at begrænse antallet af bekræftende hypoteser alvorligt. Selv om det er gyldigt at bruge statistiske test på hypoteser, der er foreslået af dataene, bør P-værdierne kun bruges som retningslinjer, og resultaterne behandles som foreløbige indtil de bekræftes af efterfølgende undersøgelser. En nyttig vejledning er at bruge en Bonferroni-korrektion, der siger, at hvis man tester n uafhængige hypoteser, skal man bruge et signifikansniveau på 0,05 / n. Hvis der således var to uafhængige hypoteser, ville et resultat kun blive erklæret signifikant, hvis P < 0,025. Bemærk, at da test sjældent er uafhængige, er dette en meget konservativ procedure – dvs. en der sandsynligvis ikke afviser nulhypotesen. Efterforskeren skulle så spørge “er dataene uafhængige?” Dette kan være vanskeligt at beslutte, men som en tommelfingerregel er resultater på den samme person eller fra matchede individer ikke uafhængige. Resultater fra et crossover-forsøg eller fra en case-control-undersøgelse, hvor kontrollerne blev matchet med tilfældene efter alder, køn og social klasse, er således ikke uafhængige.

• Analyse skal afspejle designet , og så skal et matchet design efterfølges af en matchet analyse.
• Resultater målt over tid kræver særlig omhu. En af de mest almindelige fejl i statistisk analyse er at behandle korrelerede variabler som om de var uafhængige. Antag for eksempel, at vi så på behandling af bensår, hvor nogle mennesker havde et sår på hvert ben. Vi har muligvis 20 forsøgspersoner med 30 sår, men antallet af uafhængige oplysninger er 20, fordi sårstilstanden på hvert ben for en person kan være påvirket af personens tilstand og en analyse, der betragtes sår som uafhængige observationer ville være forkert. For en korrekt analyse af blandet parret og uparret
  data, kontakt en statistiker.

Det næste spørgsmål er “hvilke typer data måles?” Den anvendte test skal bestemmes af dataene. Valget af test for matchede eller parrede data er beskrevet i tabel 1 og for uafhængige data i tabel 2.

Tabel 1 Valg af statistisk test fra parret eller matchet observation

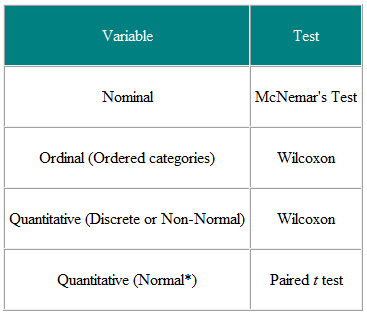
Det er nyttigt at bestemme inputvariablerne og resultatvariablerne. For eksempel er inputvariablen i et klinisk forsøg typen af behandling – en nominel variabel – og resultatet kan være et klinisk mål, måske normalt fordelt. Den krævede test er derefter t-testen (tabel 2). Imidlertid, hvis inputvariablen er kontinuerlig, siger en klinisk score, og resultatet er nominelt, siger helbredt eller ikke helbredt, er logistisk regression den krævede analyse. En t-test i dette tilfælde kan hjælpe, men vil ikke give os, hvad vi har brug for, nemlig sandsynligheden for en kur mod en given værdi af den kliniske score. Antag som et andet eksempel, at vi har en tværsnitsundersøgelse, hvor vi spørger et tilfældigt udsnit af mennesker, om de mener, at deres praktiserende læge gør et godt stykke arbejde på en fem-skala skala, og vi ønsker at fastslå, om kvinder har en højere mening af praktiserende læger end mænd har. Inputvariablen er køn, hvilket er nominelt. Resultatvariablen er den fem-punkts ordinære skala. Hver persons mening er uafhængig af de andre, så vi har uafhængige data. Fra tabel 2 skal vi bruge en χ2-test for trend eller en Mann-Whitney U-test med en korrektion for bånd (NB et bånd opstår, hvor to eller flere værdier er de samme, så der er ingen strengt stigende rækkefølge – hvor dette sker, kan man gennemsnitlig rangere for bundne værdier. Bemærk dog, at hvis nogle mennesker deler en praktiserende læge og andre ikke, så er dataene ikke uafhængig, og der kræves en mere sofistikeret analyse. Bemærk, at disse tabeller kun skal betragtes som vejledninger, og at hvert tilfælde skal betragtes efter sin fordel.

Tabel 2 Valg af statistisk test til uafhængige observationer

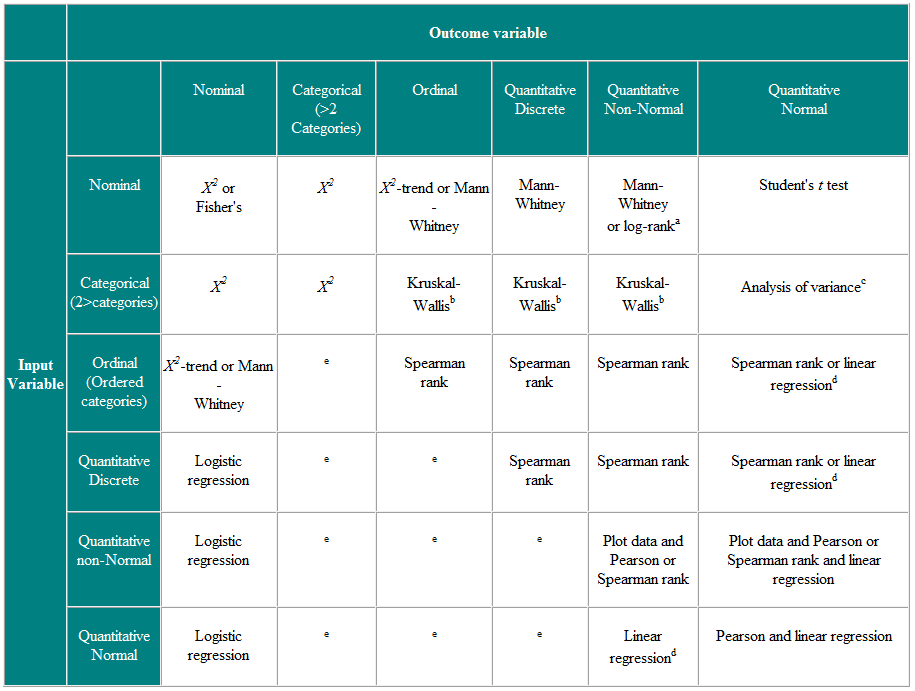
a Hvis data er censureret. b Kruskal-Wallis-testen bruges til at sammenligne ordinære eller ikke-normale variabler for mere end to grupper og er en generalisering af Mann-Whitney U-testen. c Variansanalyse er en generel teknik, og en version (envejs variansanalyse) bruges til at sammenligne normalt distribuerede variabler i mere end to grupper og er den parametriske ækvivalent til Kruskal-Wallistest. d Hvis udfaldsvariablen er den afhængige variabel, så forudsat at resterne (forskellene mellem de observerede værdier og de forudsagte svar fra regression) er sandsynligt Normalt fordelt, så er fordelingen af den uafhængige variabel ikke vigtig. e Der er en række mere avancerede teknikker, såsom Poisson-regression, til håndtering af disse situationer. Imidlertid kræver de visse antagelser, og det er ofte lettere at enten dikotomisere resultatvariablen eller behandle den som kontinuerlig.

Parametriske tests er dem, der antager antagelser om parametrene for den befolkningsfordeling, hvorfra prøven er trukket. . Dette er ofte antagelsen om, at befolkningsdataene normalt er fordelt. Ikke-parametriske tests er “distributionsfri” og kan som sådan bruges til ikke-normale variabler. Tabel 3 viser den ikke-parametriske ækvivalent af et antal parametriske tests.

Tabel 3 Parametrisk og Ikke-parametriske tests til sammenligning af to eller flere grupper

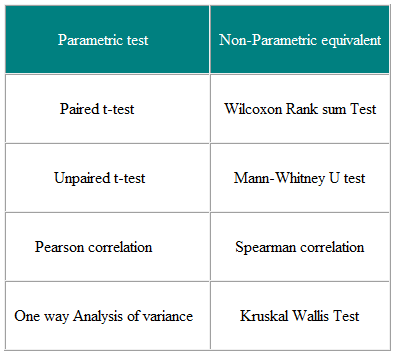
Ikke-parametriske tests er gyldige for både ikke-normalt distribuerede data og Normalt distribuerede data, så hvorfor ikke bruge dem hele tiden?

Det ser ud til at være klogt at bruge ikke-parametriske tests i alle tilfælde, hvilket vil spare en for at teste for normalitet. Parametriske tests foretrækkes, dog af følgende grunde:

1. Vi er sjældent interesserede i en signifikanstest alene; vi vil gerne sige noget om den population, hvorfra prøverne kom, og det gøres bedst med
estimater af parametre og konfidensintervaller.

2. Det er vanskeligt at udføre fleksibel modellering med ikke-parametriske tests, for eksempel at muliggøre forvirrende faktorer ved hjælp af flere regression.

3. Parametriske tests har normalt mere statistisk styrke end deres ikke-parametriske ækvivalenter. Med andre ord er det mere sandsynligt, at man opdager signifikante forskelle, når
de virkelig findes.

Sammenligner ikke-parametriske tests medianer?

Det er en almindelig opfattelse, at en Mann-Whitney U-test er faktisk en test for forskelle i medianer. Imidlertid kunne to grupper have den samme median og alligevel have en signifikant Mann-Whitney U-test. Overvej følgende data for to grupper, hver med 100 observationer. Gruppe 1: 98 (0), 1, 2; Gruppe 2: 51 (0), 1, 48 (2). Medianen er i begge tilfælde 0, men fra Mann-Whitney-testen P < 0,0001. Kun hvis vi er villige til at antage den yderligere antagelse, at forskellen i de to grupper simpelthen er et skift i placering (det vil sige, at fordelingen af data i en gruppe simpelthen forskydes med et fast beløb fra den anden) kan vi sige, at testen er en test af forskellen i medianer. Men hvis grupperne har den samme fordeling, vil et skift i placering flytte medianer og midler med samme mængde, og forskellen i medianer er således den samme som forskellen i gennemsnit. Således er Mann-Whitney U-testen også en test for forskellen i midler. Hvordan er Mann-Whitney U-testen relateret til t-testen? Hvis man skulle indtaste rækken af data snarere end selve dataene i et to-prøve t-testprogram, ville den opnåede P-værdi være meget tæt på den, der blev produceret af en Mann-Whitney U-test.