Die Steilheit eines Hügels wird als Steigung bezeichnet. Gleiches gilt für die Steilheit einer Linie. Die Steigung ist definiert als das Verhältnis der vertikalen Änderung zwischen zwei Punkten, dem Anstieg, zur horizontalen Änderung zwischen denselben beiden Punkten, dem Lauf.

$$ Steigung = \ frac {Anstieg} {Lauf} = \ frac {change \: in \: y} {change \: in \: x} $$

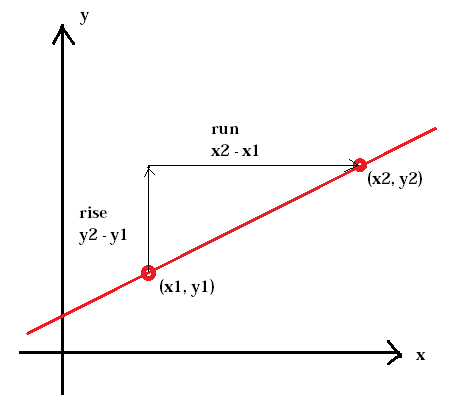
Die Die Steigung einer Linie wird normalerweise durch den Buchstaben m dargestellt. (x1, y1) repräsentiert den ersten Punkt, während (x2, y2) den zweiten Punkt repräsentiert.

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2 } \, -x_ {1}} $$

Es ist wichtig, die x- und y-Koordinaten sowohl im Zähler als auch im Nenner in derselben Reihenfolge zu halten, da sonst die falsche Steigung angezeigt wird.

Beispiel

Ermitteln Sie die Steigung der Linie

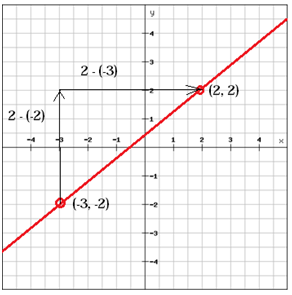
(x1, y1 ) = (-3, -2) und (x2, y2) = (2, 2)

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ { 2} \, -x_ {1}} = \ frac {2- \ left (-2 \ right)} {2- \ left (-3 \ right)} = \ frac {2 + 2} {2 + 3} = \ frac {4} {5} $$

Eine Linie mit einer positiven Steigung (m > 0) steigt als obige Linie von links nach links an rechts, während eine Linie mit einer negativen Steigung (m < 0) von links nach rechts fällt.

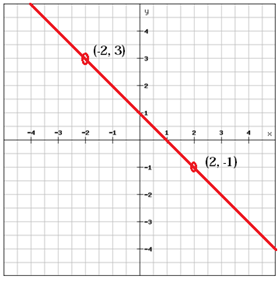
$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2} \, -x_ {1}} = \ frac {\ left (-1 \ right) -3} {2- \ left (-2 \ right)} = \ frac {-1-3} {2 + 2} = \ frac {-4} {4} = – 1 $$

Wenn zwei Linien die gleiche Steigung haben, werden die Linien als p bezeichnet parallel.

Sie können eine lineare Funktion mithilfe der Steigungsschnittform ausdrücken.

$$ y = mx + b $$

$$ m = Steigung $ $

$$ b = y – Intercept $$

Videolektion

Finden Sie die Steigung