• K-Nehest Neighbor es uno de los algoritmos de aprendizaje automático más simples basados en en la técnica de aprendizaje supervisado.
• El algoritmo K-NN asume la similitud entre el nuevo caso / datos y los casos disponibles y coloca el nuevo caso en la categoría que es más similar a las categorías disponibles.

K-NN almacena todos los datos disponibles y clasifica un nuevo punto de datos según la similitud. Esto significa que cuando aparecen nuevos datos, se pueden clasificar fácilmente en una categoría de conjunto de pozos utilizando el algoritmo K-NN.

• El algoritmo K-NN se puede utilizar tanto para la regresión como para la clasificación, pero principalmente se utiliza para los problemas de clasificación.
• K-NN es un algoritmo no paramétrico, lo que significa no hace ninguna suposición sobre los datos subyacentes.
• También se denomina algoritmo de aprendizaje perezoso porque no aprende del conjunto de entrenamiento inmediatamente, sino que almacena el conjunto de datos y, en el momento de la clasificación, realiza una acción en el conjunto de datos.
• El algoritmo KNN en la fase de entrenamiento simplemente almacena el conjunto de datos y cuando obtiene nuevos datos, clasifica esos datos en una categoría que es muy similar a los nuevos datos.
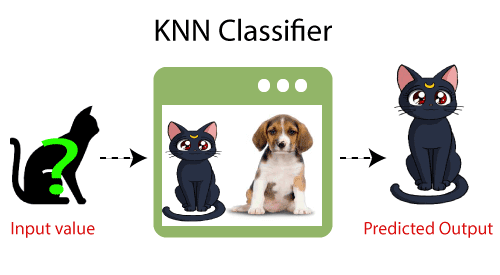
• Ejemplo: Supongamos que tenemos una imagen de una criatura que se parece a un gato y un perro, pero queremos saber si es un gato o un perro. Entonces, para esta identificación, podemos usar el algoritmo KNN, ya que funciona en una medida de similitud. Nuestro modelo KNN encontrará las características similares del nuevo conjunto de datos a las imágenes de perros y gatos y, basándose en las características más similares, las colocará en la categoría de gato o perro.

¿Por qué necesitamos un algoritmo K-NN?

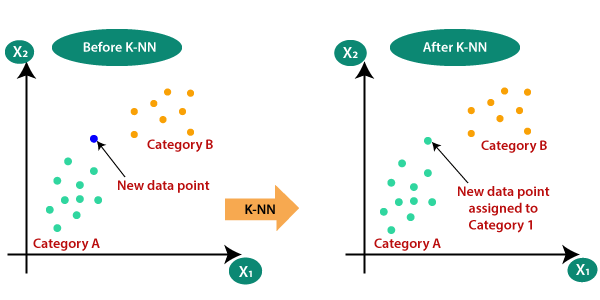
Supongamos que hay dos categorías, es decir, Categoría A y Categoría B, y tenemos un nuevo punto de datos x1, por lo que este punto de datos se ubicará en cuál de estas categorías. Para resolver este tipo de problemas, necesitamos un algoritmo K-NN. Con la ayuda de K-NN, podemos identificar fácilmente la categoría o clase de un conjunto de datos en particular. Considere el siguiente diagrama:

¿Cómo funciona K-NN?

El funcionamiento de K-NN se puede explicar sobre la base de el siguiente algoritmo:

• Paso 1: Seleccione el número K de vecinos
• Paso 2: Calcule la distancia euclidiana de K número de vecinos
• Paso 3: Tome los K vecinos más cercanos según la distancia euclidiana calculada.
• Paso 4: Entre estos k vecinos, cuente el número de puntos de datos en cada categoría.
• Paso 5: Asigne los nuevos puntos de datos a esa categoría para la que el número de vecinos sea máximo.
• Paso 6: Nuestro modelo está listo.

Suponga que tenemos un nuevo punto de datos y necesitamos ponerlo en la categoría requerida. Considere la siguiente imagen:

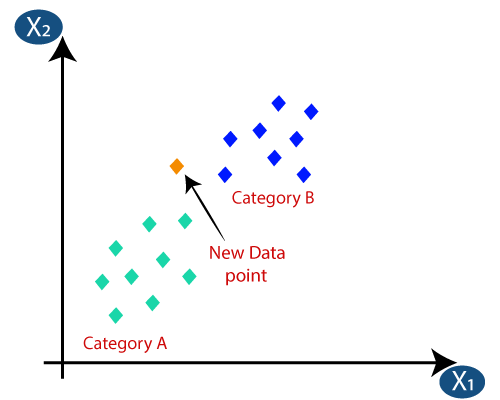
• En primer lugar, elegiremos el número de vecinos, por lo que elegiremos k = 5.
• A continuación, calcularemos la distancia euclidiana entre los puntos de datos. La distancia euclidiana es la distancia entre dos puntos, que ya hemos estudiado en geometría. Se puede calcular como:

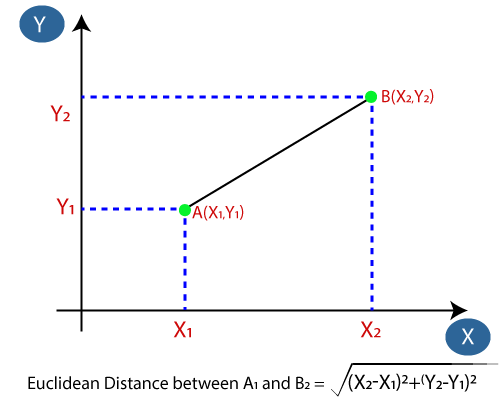
• Al calcular la distancia euclidiana obtuvimos los vecinos más cercanos, como tres vecinos más cercanos en la categoría A y dos vecinos más cercanos en la categoría B. Considere la siguiente imagen:

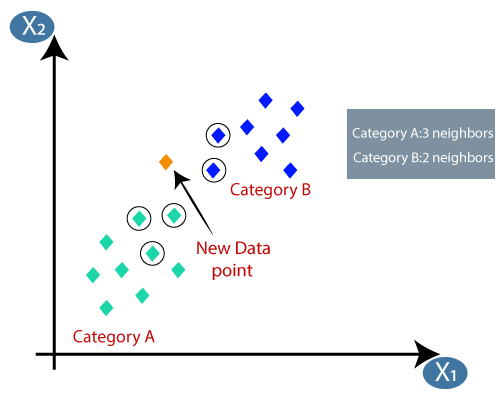
• Como podemos ver, los 3 vecinos más cercanos son de la categoría A, por lo tanto, este nuevo punto de datos debe pertenecer a la categoría A.

¿Cómo seleccionar el valor de K en el algoritmo K-NN?

A continuación se muestran algunos puntos para recuerde al seleccionar el valor de K en el algoritmo K-NN:

• No hay una forma particular de determinar el mejor valor para «K», por lo que debemos probar algunos valores para encontrar el mejor fuera de ellos. El valor más preferido para K es 5.
• Un valor muy bajo para K, como K = 1 o K = 2, puede ser ruidoso y provocar los efectos de valores atípicos en el modelo.
• Los valores altos para K son buenos, pero pueden encontrar algunas dificultades.

Ventajas del algoritmo KNN:

• Es simple de implementar.
• Es robusto para los datos de entrenamiento ruidosos
• Puede ser más efectivo si los datos de entrenamiento son grandes.

Desventajas del algoritmo KNN:

• Siempre necesita determinar el valor de K, que puede ser complejo en algún momento.
• El costo de cálculo es alto debido al cálculo de la distancia entre los puntos de datos para todas las muestras de entrenamiento. .

Implementación Python del algoritmo KNN

Para realizar la implementación Python del algoritmo K-NN, usaremos el mismo problema y conjunto de datos que hemos usado en Regresión logística. Pero aquí mejoraremos el rendimiento del modelo. A continuación se muestra la descripción del problema:

Problema del algoritmo K-NN: hay una empresa fabricante de automóviles que ha fabricado un nuevo automóvil SUV.La empresa quiere dar los anuncios a los usuarios que estén interesados en comprar ese SUV. Entonces, para este problema, tenemos un conjunto de datos que contiene información de múltiples usuarios a través de la red social. El conjunto de datos contiene mucha información, pero el salario y la edad estimados los consideraremos para la variable independiente y la variable Comprada es para la variable dependiente. A continuación se muestra el conjunto de datos:

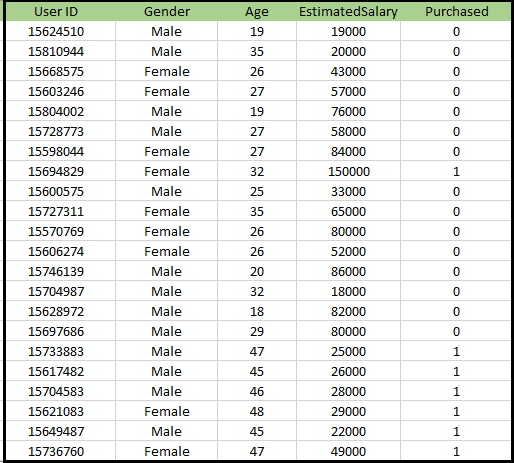
Pasos para implementar el algoritmo K-NN:

• Paso de preprocesamiento de datos
• Ajustar el algoritmo K-NN al conjunto de entrenamiento
• Predecir el resultado de la prueba
• Exactitud de la prueba del resultado (Creación de matriz de confusión)
• Visualización del resultado del conjunto de prueba.

Paso de preprocesamiento de datos:

El paso de preprocesamiento de datos seguirá siendo exactamente el mismo que el de Regresión logística. A continuación se muestra el código para ello:

Al ejecutar el código anterior, nuestro conjunto de datos se importa a nuestro programa y está bien preprocesado. Después de escalar las características, nuestro conjunto de datos de prueba se verá así:

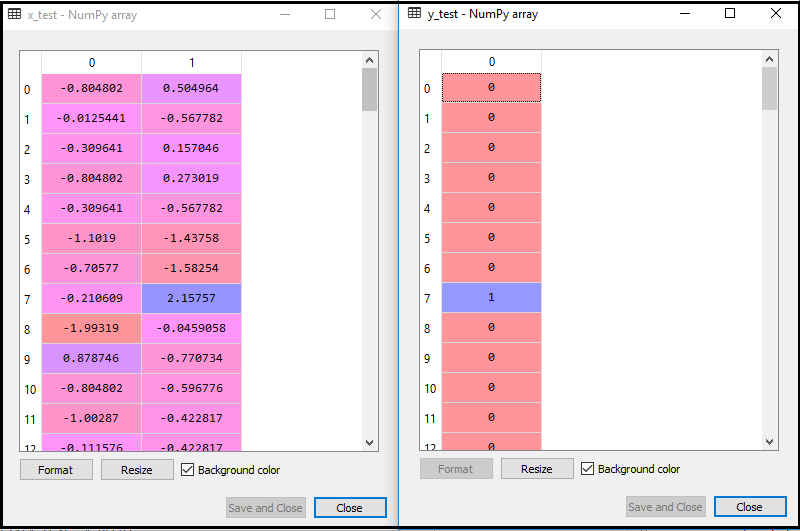
De la salida anterior im edad, podemos ver que nuestros datos se escalan correctamente.

• Adaptando el clasificador K-NN a los datos de entrenamiento:
  Ahora ajustaremos el clasificador K-NN a los datos de entrenamiento. Para hacer esto, importaremos la clase KNeighborsClassifier de la biblioteca Sklearn Neighbors. Después de importar la clase, crearemos el objeto Clasificador de la clase. El parámetro de esta clase será
  • n_neighbors: Para definir los vecinos requeridos del algoritmo. Por lo general, toma 5.
  • metric = «minkowski»: Este es el parámetro predeterminado y decide la distancia entre los puntos.
  • p = 2: Es equivalente al estándar Métrica euclidiana.

  Y luego ajustaremos el clasificador a los datos de entrenamiento. A continuación se muestra el código para ello:

Salida: Al ejecutar el código anterior, obtendremos la salida como:

• Predecir el resultado de la prueba: Para predecir el resultado del conjunto de prueba, crearemos un vector y_pred como hicimos en Regresión logística. A continuación se muestra el código para ello:

Salida:

La salida para el código anterior será:

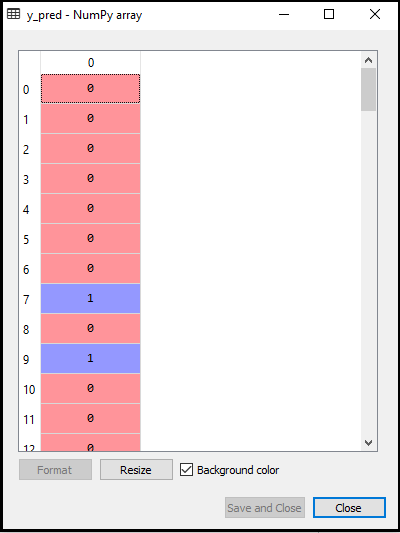
• Creando la Matriz de Confusión:
  Ahora crearemos la Matriz de Confusión para nuestro modelo K-NN para ver la precisión del clasificador. A continuación se muestra el código para ello:

En el código anterior, hemos importado la función confusion_matrix y la hemos llamado usando la variable cm.

Salida: Al ejecutar el código anterior, obtendremos la matriz como se muestra a continuación:

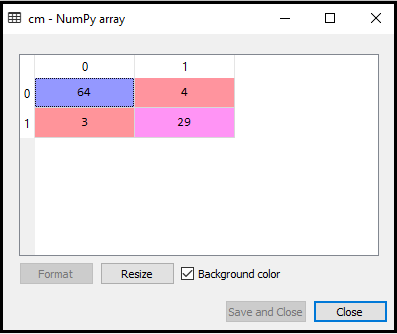
En la imagen de arriba, podemos ver hay 64 + 29 = 93 predicciones correctas y 3 + 4 = 7 predicciones incorrectas, mientras que, en Regresión logística, hubo 11 predicciones incorrectas. Entonces podemos decir que el rendimiento del modelo se mejora mediante el uso del algoritmo K-NN.

• Visualización del resultado del conjunto de entrenamiento:
  Ahora, visualizaremos el resultado del conjunto de entrenamiento para K -Modelo NN. El código seguirá siendo el mismo que hicimos en Regresión logística, excepto el nombre del gráfico. A continuación se muestra el código para ello:

Salida:

Al ejecutar el código anterior, obtendremos el siguiente gráfico:

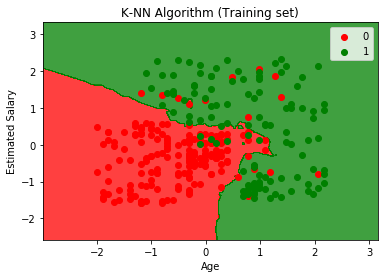
La gráfica de salida es diferente a la gráfica que hemos ocurrido en Regresión logística. Se puede entender en los siguientes puntos:

• Como podemos ver, el gráfico muestra el punto rojo y los puntos verdes. Los puntos verdes son para la variable Comprado (1) y los Puntos rojos para la variable No comprado (0).
• El gráfico muestra un límite irregular en lugar de mostrar cualquier línea recta o cualquier curva porque es un algoritmo K-NN, es decir, encontrar el vecino más cercano.
• El gráfico ha clasificado a los usuarios en las categorías correctas, ya que la mayoría de los usuarios que no compraron el SUV están en la región roja y los usuarios que compraron el SUV están en la región verde.
• El gráfico muestra un buen resultado, pero aún así, hay algunos puntos verdes en la región roja y puntos rojos en la región verde. Pero esto no es un gran problema ya que al hacer este modelo se evita problemas de sobreajuste.
• Por lo tanto, nuestro modelo está bien entrenado.
• Visualización del resultado del conjunto de prueba:
  Después del entrenamiento del modelo, ahora probaremos el resultado poniendo un nuevo conjunto de datos, es decir, Conjunto de datos de prueba. El código sigue siendo el mismo, excepto algunos cambios menores: como x_train y y_train serán reemplazados por x_test e y_test.
  A continuación se muestra el código:

Resultado:

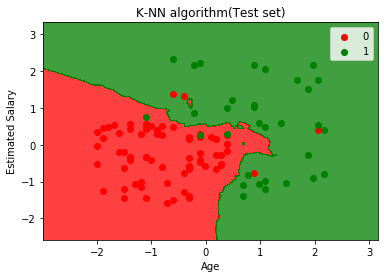
El gráfico anterior muestra el resultado del conjunto de datos de prueba. Como podemos ver en el gráfico, el resultado predicho es bueno bueno ya que la mayoría de los puntos rojos están en la región roja y la mayoría de los puntos verdes están en la región verde.

Sin embargo, hay pocos puntos verdes en la región roja y algunos puntos rojos en la región verde. Entonces estas son las observaciones incorrectas que hemos observado en la matriz de confusión (7 Salida incorrecta).