Cálculos de fuerza

La fuerza es empujar o tirar.
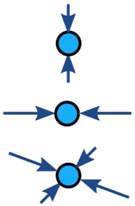
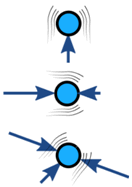
Las fuerzas sobre un objeto generalmente están equilibradas (si no está equilibrado, el objeto acelera):
 |
 |
|
| Equilibrado | Desequilibrado | |
|---|---|---|
| Sin aceleración | Aceleración |
Ejemplo: las fuerzas en la parte superior de esta torre de puente están en equilibrio (no se acelera):

Los cables tiran hacia abajo por igual a la izquierda y a la derecha, y eso se equilibra con el empuje hacia arriba de la torre. (¿La torre empuja? ¡Sí! Imagínese que está parado allí en lugar de la torre.)
Podemos modelar las fuerzas así:

Y cuando ponerlos de cabeza a cola, vemos que se cierran sobre sí mismos, lo que significa que el efecto neto es cero:

Las fuerzas están en equilibrio.
Se dice que las fuerzas en equilibrio están en equilibrio: tampoco hay cambios en el movimiento.
Diagramas de cuerpo libre
El primer paso es para dibujar un diagrama de cuerpo libre (también llamado diagrama de fuerza)
Diagrama de cuerpo libre: un boceto en el que un cuerpo se separa del mundo excepto por las fuerzas que actúan sobre él.
En el ejemplo del puente, el diagrama de cuerpo libre para la parte superior de la torre es:

Diagrama de cuerpo libre
Ayuda pensemos claramente en las fuerzas que actúan sobre el cuerpo.
Ejemplo: automóvil en una carretera
¿Cuáles son las fuerzas en un automóvil que circula por la autopista?

El motor está trabajando duro, entonces, ¿por qué el auto no sigue acelerando?
Porque la conducción la fuerza se equilibra con:
- Resistencia del aire (en pocas palabras: th El aire resiste ser empujado),
- Resistencia a la rodadura, también llamada fricción de rodadura (los neumáticos resisten que su forma cambie)

Diagrama de carrocería libre
W es el peso del coche,
R1 y R2 son la resistencia a la rodadura de los neumáticos,
N1 y N2 son las fuerzas de reacción (equilibrando el peso del coche).
Nota: las ruedas de acero (como en los trenes) tienen menos resistencia a la rodadura, ¡pero son demasiado resbaladizas en la carretera!
Cálculos
La fuerza es un vector. Un vector tiene magnitud (tamaño) y dirección:

Podemos modelar las fuerzas dibujando flechas del tamaño y dirección correctos . Así:
Ejemplo: Admirar la vista
Brady se para en el borde de un balcón sostenido por una viga horizontal y un puntal:

Pesa 80 kg.
¿Cuáles son las fuerzas?
Tomemos el lugar en el que está parado y pensemos en las fuerzas que se encuentran allí:

Su peso
Su masa de 80 kg crea una fuerza descendente debido a la gravedad.
La fuerza es la masa multiplicada por la aceleración: F = ma
La aceleración debida a la gravedad en la Tierra es de 9,81 m / s2 , entonces a = 9.81 m / s2
F = 80 kg × 9.81 m / s2
F = 785 N
Las otras fuerzas
Las fuerzas están equilibradas, por lo que deberían volver a cerrarse sobre sí mismas así:

Podemos usar trigonometría para resolverlo .
Debido a que es un triángulo rectángulo, SOHCAHTOA ayudará.
Para la Viga, conocemos el Adyacente, queremos conocer el Opuesto, y «TOA» nos dice que usemos la Tangente:
bronceado (60 ° ) = Haz / 785 N
Haz / 785 N = tan (60 °)
Haz = tan (60 °) × 785 N
Haz = 1.732 … × 785 N = 1360 N
Para el Strut, conocemos el Adyacente, queremos conocer la Hipotenusa y «CAH» nos dice que usemos Coseno:
cos (60 °) = 785 N / Strut
Strut × cos (60 °) = 785 N
Strut = 785 N / cos (60 °)
Strut = 785 N / 0.5 = 1570 N
Resuelto:

Interesante cuánta fuerza hay en la viga y el puntal en comparación con el peso que se soporta!
Torque (o Momento)
¿Qué pasa si la viga simplemente está pegada a la pared (llamada voladizo)?

No hay un puntal de apoyo, entonces, ¿qué sucede con las fuerzas?
El diagrama de cuerpo libre se ve así:

La fuerza hacia arriba R equilibra el peso hacia abajo.
Con solo esos dos fuerzas, el rayo girará como una hélice. Pero también hay un «efecto de giro» M llamado Momento (o Torque) que lo equilibra:
Momento: Fuerza multiplicada por la Distancia en ángulos rectos.
Sabemos que el Peso es 785 N, y también necesitamos saber la distancia en ángulo recto, que en este caso es de 3,2 m.
M = 785 N x 3,2 m = 2512 Nm
Y ese momento es lo que impide que el rayo gire.

Puedes sentir el momento cuando agarras una caña de pescar.
Además de sostener su peso, debes evitar que gire hacia abajo.
Fricción
Caja en una rampa
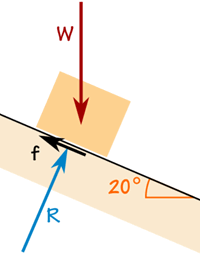
La caja pesa 100 kg.
La fuerza de fricción es suficiente para mantenerla donde está.
La fuerza de reacción R está en ángulo recto con la rampa.
La caja no acelera, por lo que las fuerzas están en equilibrio:
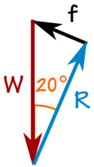
El 100 kg de masa crea una fuerza hacia abajo debido a la gravedad:
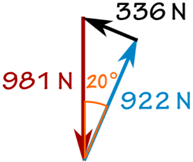
W = 100 kg × 9.81 m / s2 = 981 N
Podemos usar SOHCAHTOA para resolver el triángulo.
Fricción f:
sin (20 °) = f / 981 N
f = sin (20 °) × 981 N = 336 N
Reacción N:
cos (20 °) = R / 981 N
R = cos (20 °) × 981 N = 922 N
Y obtenemos:
Consejos para dibujar diagramas de cuerpo libre
- Dibuje de la forma más sencilla posible. Una caja suele ser suficiente.
- Las fuerzas apuntan en la dirección en que actúan sobre el cuerpo
- flechas rectas para las fuerzas
- flechas curvas por momentos
Sam y Alex Pull a Box
Los cálculos a veces pueden ser más fáciles cuando convertimos la magnitud y la dirección en xey:
 |
< = > |  |
| Vector a en coordenadas polares |
Vector a en coordenadas cartesianas |
Puede leer cómo convertirlos en polar y cartesiano Coordenadas, pero aquí hay un resumen rápido:
¡Vamos a usarlas!