Pruebas paramétricas y no paramétricas para comparar dos o más grupos

Estadísticas: pruebas paramétricas y no paramétricas

Esta sección abarca:

• Elección de una prueba
• Pruebas paramétricas
• Pruebas no paramétricas

Elección de una prueba

En términos de seleccionar una prueba estadística, la pregunta más importante es «¿cuál es la principal hipótesis del estudio?» En algunos casos no hay hipótesis; el investigador solo quiere «ver lo que hay». Por ejemplo, en un estudio de prevalencia no hay hipótesis para probar y el tamaño del estudio está determinado por la precisión con la que el investigador desea determinar la prevalencia. Si no hay hipótesis, entonces no hay prueba estadística. Es importante decidir a priori qué hipótesis son confirmatorias (es decir, están probando alguna relación supuesta) y cuáles son exploratorias (son sugeridas por los datos). Ningún estudio por sí solo puede respaldar toda una serie de hipótesis. Un plan sensato es limitar severamente el número de hipótesis confirmatorias. Si bien es válido utilizar pruebas estadísticas sobre las hipótesis sugeridas por los datos, los valores de P deben usarse solo como pautas, y los resultados deben tratarse como provisionales hasta que sean confirmados por estudios posteriores. Una guía útil es usar una corrección de Bonferroni, que establece simplemente que si uno está probando n hipótesis independientes, debe usar un nivel de significancia de 0.05 / n. Por lo tanto, si hubiera dos hipótesis independientes, un resultado se declararía significativo solo si P < 0.025. Tenga en cuenta que, dado que las pruebas rara vez son independientes, este es un procedimiento muy conservador, es decir, que es poco probable que rechace la hipótesis nula. A continuación, el investigador debería preguntar «¿son los datos independientes?» Esto puede ser difícil de decidir pero, como regla general, los resultados en el mismo individuo o en individuos emparejados no son independientes. Por lo tanto, los resultados de un ensayo cruzado o de un estudio de casos y controles en el que los controles se emparejaron con los casos por edad, sexo y clase social, no son independientes.

• El análisis debe reflejar el diseño , por lo que un diseño emparejado debe ir seguido de un análisis emparejado.
• Los resultados medidos a lo largo del tiempo requieren un cuidado especial. Uno de los errores más comunes en el análisis estadístico es tratar las variables correlacionadas como si fueran independientes. Por ejemplo, supongamos que estamos analizando el tratamiento de las úlceras en las piernas, en las que algunas personas tienen una úlcera en cada pierna. Podríamos tener 20 sujetos con
  30 úlceras, pero la cantidad de datos independientes es 20 porque el estado de las úlceras en cada pierna de una persona puede estar influenciado por el estado de
  salud de la persona y un análisis que consideradas úlceras como observaciones independientes serían incorrectas. Para un análisis correcto de datos
  pareados y no pareados, consulte a un estadístico.

La siguiente pregunta es «¿qué tipos de datos se están midiendo?» La prueba utilizada debe estar determinada por los datos. La elección de la prueba para datos emparejados o emparejados se describe en la Tabla 1 y para los datos independientes en la Tabla 2.

Tabla 1 Elección de prueba estadística de observación emparejada o emparejada

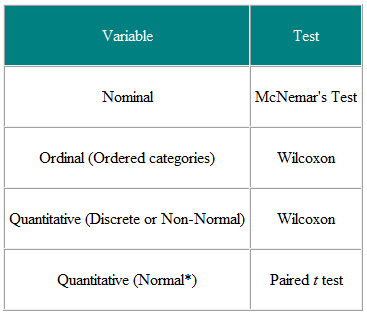
Es útil decidir las variables de entrada y las variables de resultado. Por ejemplo, en un ensayo clínico, la variable de entrada es el tipo de tratamiento, una variable nominal, y el resultado puede ser alguna medida clínica, quizás normalmente distribuida. La prueba requerida es entonces la prueba t (Tabla 2). Sin embargo, si la variable de entrada es continua, digamos una puntuación clínica, y el resultado es nominal, digamos curado o no curado, la regresión logística es el análisis requerido. En este caso, una prueba t puede ayudar pero no nos daría lo que necesitamos, es decir, la probabilidad de curación para un valor dado de la puntuación clínica. Como otro ejemplo, supongamos que tenemos un estudio transversal en el que preguntamos a una muestra aleatoria de personas si creen que su médico de cabecera está haciendo un buen trabajo, en una escala de cinco puntos, y deseamos determinar si las mujeres tienen una opinión más alta. de los médicos generales que los hombres. La variable de entrada es el género, que es nominal. La variable de resultado es la escala ordinal de cinco puntos. La opinión de cada persona es independiente de las demás, por lo que tenemos datos independientes. De la Tabla 2 deberíamos usar una prueba χ2 para la tendencia, o una prueba U de Mann-Whitney con una corrección para los empates (NB, un empate ocurre cuando dos o más los valores son los mismos, por lo que no hay un orden estrictamente creciente de rangos; cuando esto sucede, se puede promediar los rangos para valores vinculados). Sin embargo, tenga en cuenta que si algunas personas comparten un médico general y otras no, los datos no son Se requiere un análisis independiente y más sofisticado Tenga en cuenta que estas tablas deben considerarse solo como guías, y cada caso debe considerarse en sus méritos.

Tabla 2 Elección de prueba estadística para observaciones independientes

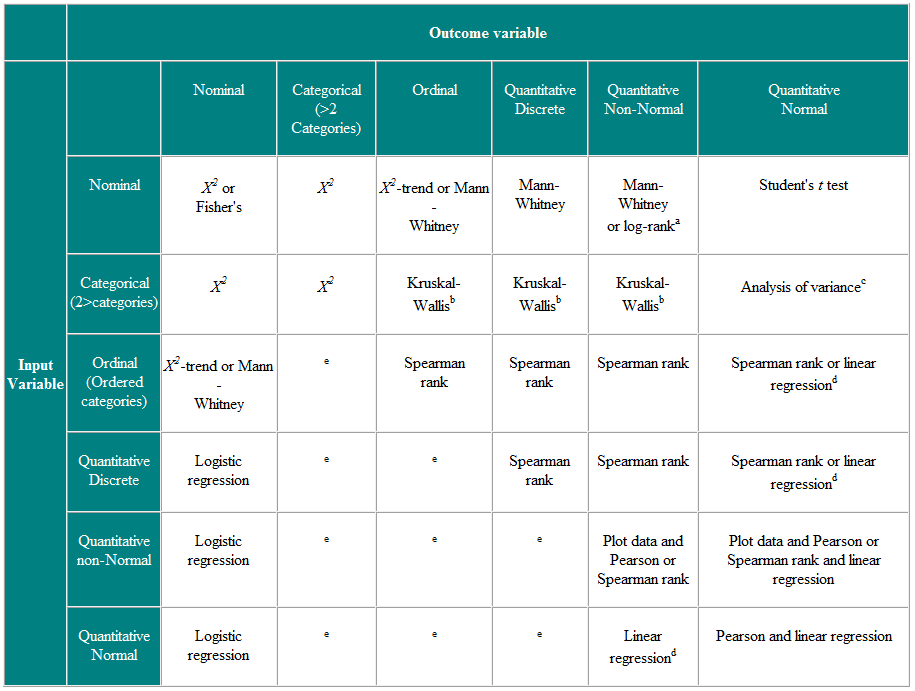
a Si los datos están censurados. b La prueba de Kruskal-Wallis se utiliza para comparar variables ordinales o no normales para más de dos grupos y es una generalización de la prueba U de Mann-Whitney. c El análisis de varianza es una técnica general, y se utiliza una versión (análisis de varianza de una vía) para comparar variables distribuidas normalmente para más de dos grupos, y es el equivalente paramétrico de Kruskal-Wallistest. d Si la variable de resultado es la variable dependiente, siempre que los residuos (las diferencias entre los valores observados y las respuestas predichas de la regresión) tengan una distribución normal plausible, entonces la distribución de la variable independiente no es importante. e Hay varias técnicas más avanzadas, como la regresión de Poisson, para tratar estas situaciones. Sin embargo, requieren ciertas suposiciones y, a menudo, es más fácil dicotomizar la variable de resultado o tratarla como continua.

Las pruebas paramétricas son aquellas que hacen suposiciones sobre los parámetros de la distribución de la población de la que se extrae la muestra. . Suele suponerse que los datos de población se distribuyen normalmente. Las pruebas no paramétricas son «libres de distribución» y, como tales, se pueden utilizar para variables no normales. La Tabla 3 muestra el equivalente no paramétrico de una serie de pruebas paramétricas.

Tabla 3 Paramétricas y Pruebas no paramétricas para comparar dos o más grupos

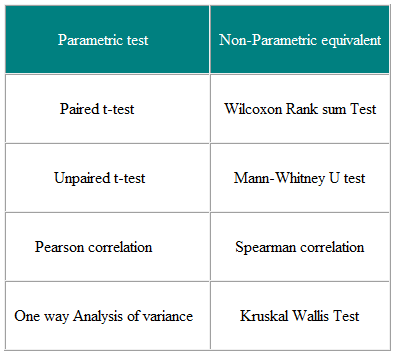
Las pruebas no paramétricas son válidas tanto para datos distribuidos normalmente como para Datos normalmente distribuidos, ¿por qué no usarlos todo el tiempo?

Parecería prudente usar pruebas no paramétricas en todos los casos, lo que evitaría la molestia de probar la normalidad. Se prefieren las pruebas paramétricas, sin embargo, por las siguientes razones:

1. Rara vez estamos interesados en una prueba de significancia sola; nos gustaría decir algo sobre la población de la que provienen las muestras, y esto se hace mejor con
estimaciones de parámetros e intervalos de confianza.

2. Es difícil hacer modelos flexibles con pruebas no paramétricas, por ejemplo, permitiendo factores de confusión utilizando múltiples regresión.

3. Las pruebas paramétricas suelen tener más poder estadístico que sus equivalentes no paramétricos. En otras palabras, es más probable que se detecten diferencias significativas cuando
realmente existen.

¿Las pruebas no paramétricas comparan medianas?

Es una creencia común que un La prueba U de Mann-Whitney es de hecho una prueba de diferencias en las medianas. Sin embargo, dos grupos podrían tener la misma mediana y aún tener una prueba U de Mann-Whitney significativa. Considere los siguientes datos para dos grupos, cada uno con 100 observaciones. Grupo 1: 98 (0), 1, 2; Grupo 2:51 (0), 1, 48 (2). La mediana en ambos casos es 0, pero de la prueba de Mann-Whitney P < 0,0001. Solo si estamos preparados para hacer el supuesto adicional de que la diferencia en los dos grupos es simplemente un cambio de ubicación (es decir, la distribución de los datos en un grupo simplemente se desplaza en una cantidad fija del otro) podemos decir que la prueba es una prueba de la diferencia en medianas. Sin embargo, si los grupos tienen la misma distribución, entonces un cambio de ubicación moverá las medianas y las medias en la misma cantidad y, por lo tanto, la diferencia en las medianas es la misma que la diferencia en las medias. Por tanto, la prueba U de Mann-Whitney también es una prueba de la diferencia de medias. ¿Cómo se relaciona la prueba U de Mann-Whitney con la prueba t? Si se ingresaran los rangos de los datos en lugar de los datos en sí mismos en un programa de prueba t de dos muestras, el valor de P obtenido sería muy cercano al producido por una prueba U de Mann-Whitney.