MATH 1314: Álgebra universitaria
Mientras que las asíntotas verticales describen el comportamiento de una gráfica cuando la salida se vuelve muy grande o muy pequeña, las asíntotas horizontales ayudan a describir el comportamiento de una gráfica como la entrada se vuelve muy grande o muy pequeña. Recuerde que el comportamiento final de un polinomio reflejará el del término principal. Del mismo modo, el comportamiento final de una función racional reflejará el de la relación de los términos principales de las funciones numerador y denominador.
Hay tres resultados distintos al verificar las asíntotas horizontales:
Caso 1: si el grado del denominador es > grado del numerador, hay una asíntota horizontal en y = 0.

Caso 2: Si el grado del denominador < grado del numerador en uno, obtenemos una asíntota inclinada.

Observe que, mientras que la gráfica de una función racional nunca cruzará una asíntota vertical, la gráfica puede o no cruzar una horizontal o inclinada como ymptote. Además, aunque la gráfica de una función racional puede tener muchas asíntotas verticales, la gráfica tendrá como máximo una asíntota horizontal (o inclinada).
Cabe señalar que, si el grado del numerador es mayor que el grado del denominador en más de uno, el comportamiento final del gráfico imitará el comportamiento de la fracción de comportamiento final reducido. Por ejemplo, si tuviéramos la función
con comportamiento final
el comportamiento final del gráfico sería similar al de un polinomio par con un coeficiente principal positivo.
Una nota general: asíntotas horizontales de funciones racionales
La asíntota horizontal de una función racional puede ser determinado mirando los grados del numerador y el denominador.
- El grado del numerador es menor que el grado del denominador: asíntota horizontal en y = 0.
- El grado del numerador es mayor que el grado del denominador en uno: sin asíntota horizontal; asíntota inclinada.
- El grado del numerador es igual al grado del denominador: asíntota horizontal en la razón de los coeficientes principales.
Ejemplo 9: Identificación de asíntotas horizontales y verticales
Encuentre las asíntotas horizontales y verticales de la función
Solución
Primero, tenga en cuenta que esta función no tiene factores comunes, por lo que no hay discontinuidades removibles potenciales.
La función tendrá asíntotas verticales cuando el denominador es cero, lo que hace que la función no esté definida. El denominador será cero en x = 1, -2, texto {y} 5 \, lo que indica asíntotas verticales en estos valores.
El numerador tiene grado 2, mientras que el denominador tiene grado 3. Dado que el grado del denominador es mayor que el grado del numerador, el denominador crecerá más rápido que el numerador, lo que hará que las salidas tiendan hacia cero a medida que las entradas se hacen grandes, y así, como xto pm infty, fleft (xright) a 0 \. Esta función tendrá una asíntota horizontal en y = 0 \.
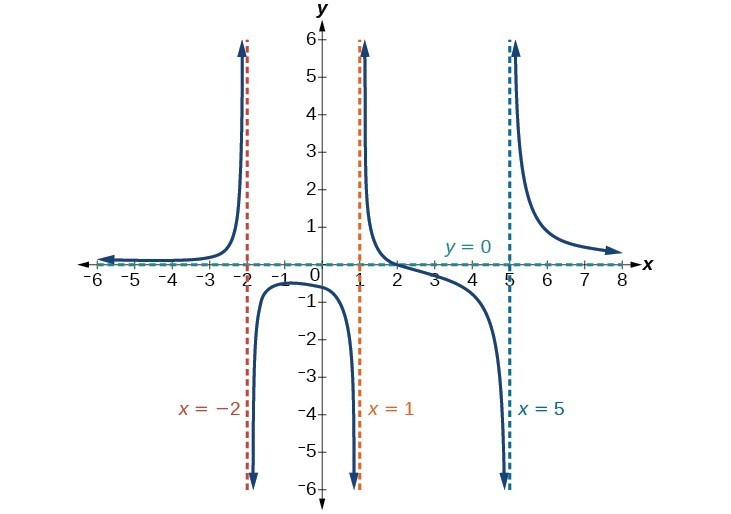
Figura 15
Una nota general: intersecciones de funciones racionales
Una función racional tendrá una intersección y cuando la entrada sea cero, si la función se define en cero. Una función racional no tendrá una intersección con el eje y si la función no está definida en cero.
Del mismo modo, una función racional tendrá intersecciones con el eje x en las entradas que hacen que la salida sea cero. Dado que una fracción solo es igual a cero cuando el numerador es cero, las intersecciones x solo pueden ocurrir cuando el numerador de la función racional es igual a cero.
Pruébelo 7
Dada la función recíproca al cuadrado que se desplaza hacia la derecha 3 unidades y hacia abajo 4 unidades, escribe esto como una función racional. Luego, encuentre las intersecciones en x e y y las asíntotas horizontal y vertical.
Solución