• K-lähin naapuri on yksi yksinkertaisimmista koneoppimisalgoritmeista valvotusta oppimistekniikasta.
• K-NN-algoritmi olettaa uuden tapauksen / datan ja käytettävissä olevien tapausten samankaltaisuuden ja sijoittaa uuden tapauksen luokkaan, joka on eniten samanlainen kuin käytettävissä olevat luokat.
• K-NN-algoritmi tallentaa kaikki käytettävissä olevat tiedot ja luokittelee uuden datapisteen samankaltaisuuden perusteella. Tämä tarkoittaa sitä, että kun uutta tietoa ilmestyy, se voidaan helposti luokitella kaivosarjaluokkaan käyttämällä K-NN-algoritmia.
• K-NN-algoritmia voidaan käyttää sekä regressioon että luokitteluun, mutta enimmäkseen sitä käytetään luokitusongelmiin.
• K-NN on ei-parametrinen algoritmi, mikä tarkoittaa se ei tee mitään oletusta taustalla olevista tiedoista.
• Sitä kutsutaan myös laiskaksi oppijan algoritmiksi, koska se ei opi koulutusjoukosta välittömästi, vaan tallentaa tietojoukon ja luokitteluhetkellä toiminto tietojoukossa.
• KNN-algoritmi koulutusvaiheessa vain tallentaa tietojoukon ja kun se saa uutta tietoa, se luokittelee nämä tiedot luokkaan, joka on paljon samanlainen kuin uudet tiedot.
• Esimerkki: Oletetaan, että meillä on kuva olentosta, joka näyttää samankaltaiselta kuin kissa ja koira, mutta haluamme tietää, onko kyseessä kissa tai koira. Joten tässä tunnistuksessa voimme käyttää KNN-algoritmia, koska se toimii samankaltaisuusmitalla. KNN-mallimme löytää uuden tietojoukon samanlaiset ominaisuudet kissojen ja koirien kuville ja sijoittaa sen vastaavimpien ominaisuuksien perusteella joko kissan tai koiran luokkaan.

Miksi tarvitsemme K-NN-algoritmin?

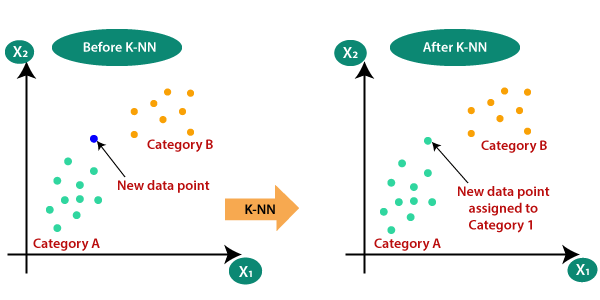
Oletetaan, että on olemassa kaksi luokkaa, eli luokka A ja luokka B, ja meillä on uusi datapiste x1, joten tämä datapiste sijaitsee missä näistä luokista. Tämäntyyppisen ongelman ratkaisemiseksi tarvitsemme K-NN-algoritmin. K-NN: n avulla voimme helposti tunnistaa tietyn tietojoukon luokan tai luokan. Harkitse seuraavaa kaaviota:

Kuinka K-NN toimii?

K-NN: n toiminta voidaan selittää alla oleva algoritmi:

• Vaihe 1: Valitse naapureiden lukumäärä K
• Vaihe 2: Laske naapureiden K lukumäärän euklidinen etäisyys
• Vaihe 3: Ota K lähimmät naapurit lasketun euklidisen etäisyyden mukaan.
• Vaihe 4: Laske näiden k naapureiden joukossa kunkin luokan datapisteiden määrä.
• Vaihe 5: Määritä uudet datapisteet siihen luokkaan, johon naapurin lukumäärä on suurin.
• Vaihe-6: Mallimme on valmis.

Oletetaan, että meillä on uusi datapiste ja meidän on lisättävä se vaadittuun luokkaan. Harkitse seuraavaa kuvaa:

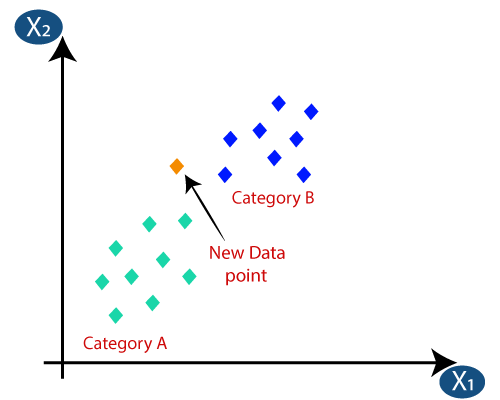
• Ensinnäkin valitaan naapureiden lukumäärä, joten valitaan k = 5.
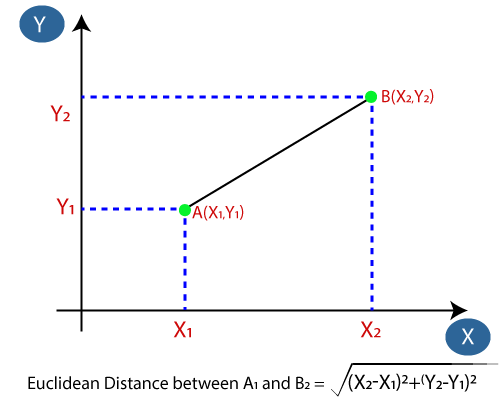
• Seuraavaksi lasketaan datapisteiden välinen euklidinen etäisyys. Euklidinen etäisyys on kahden pisteen välinen etäisyys, jota olemme jo tutkineet geometriassa. Se voidaan laskea seuraavasti:

• Laskemalla euklidisen etäisyyden saimme lähimmät naapurit, kolme lähintä naapuria kategoriassa A ja kaksi lähintä naapuria luokassa B. Harkitse alla olevaa kuvaa:

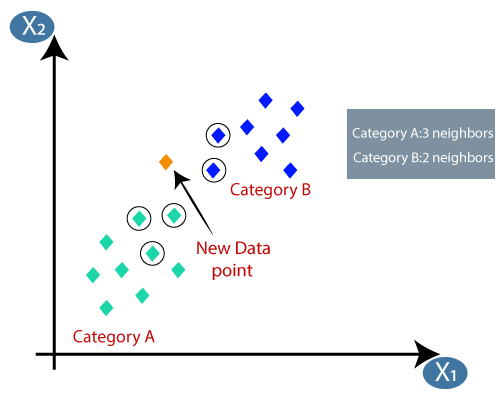
• Kuten voimme nähdä, 3 lähintä naapuria kuuluvat luokkaan A, joten tämän uuden datapisteen on kuuluttava luokkaan A.

Kuinka valita K: n arvo K-NN-algoritmissa?

Alla on joitain pisteitä muista, kun valitset K: n arvon K-NN-algoritmissa:

• K: lle parhaan arvon määrittämiseksi ei ole mitään erityistä tapaa, joten meidän on kokeiltava joitain arvoja löytääksesi parhaan pois heistä. K: n edullisin arvo on 5.
• Erittäin matala K: n arvo, kuten K = 1 tai K = 2, voi olla meluisa ja johtaa poikkeamien vaikutuksiin mallissa.
• Suuret K-arvot ovat hyviä, mutta se saattaa löytää vaikeuksia.

KNN-algoritmin edut:

• Se on helppo toteuttaa.
• Se on kestävä meluisille harjoitustiedoille
• Se voi olla tehokkaampi, jos harjoitustiedot ovat suuria.

KNN-algoritmin haitat:

• Aina on määritettävä K: n arvo, joka voi olla jonkin aikaa monimutkainen.
• Laskentakustannukset ovat korkeat, koska lasketaan kaikkien harjoitusnäytteiden datapisteiden välinen etäisyys .

KNN-algoritmin Python-toteutus

K-NN-algoritmin Python-toteutuksen suorittamiseen käytämme samaa ongelmaa ja tietojoukkoa, jota olemme käyttäneet Logistinen regressio. Mutta tässä parannamme mallin suorituskykyä. Alla on ongelman kuvaus:

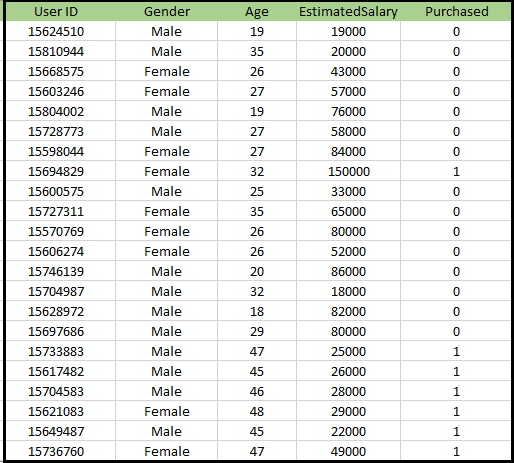
Ongelma K-NN-algoritmille: On autonvalmistaja, joka on valmistanut uuden SUV-auton.Yritys haluaa antaa mainokset käyttäjille, jotka ovat kiinnostuneita ostamaan kyseisen maastoauton. Joten tätä ongelmaa varten meillä on tietojoukko, joka sisältää useita käyttäjän tietoja sosiaalisen verkoston kautta. Aineisto sisältää paljon tietoa, mutta arvioitu palkka ja ikä, jota harkitsemme riippumattomalle muuttujalle ja Ostettu muuttuja on riippuvaiselle muuttujalle. Alla on tietojoukko:

Vaiheet K-NN-algoritmin toteuttamiseksi:

• tietojen esikäsittelyvaihe
• K-NN-algoritmin sovittaminen harjoitusjoukkoon
• Testituloksen ennustaminen
• Tuloksen testitarkkuus (Confusion-matriisin luominen)
• Testisarjan tuloksen visualisointi.

Tietojen esikäsittelyvaihe:

Tietojen esikäsittelyvaihe pysyy täsmälleen sama kuin logistinen regressio. Alla on koodi sitä varten:

Suorittamalla yllä oleva koodi tietojoukkomme tuodaan ohjelmaamme ja esikäsitellään hyvin. Ominaisuuden skaalauksen jälkeen testitietojoukko näyttää tältä:

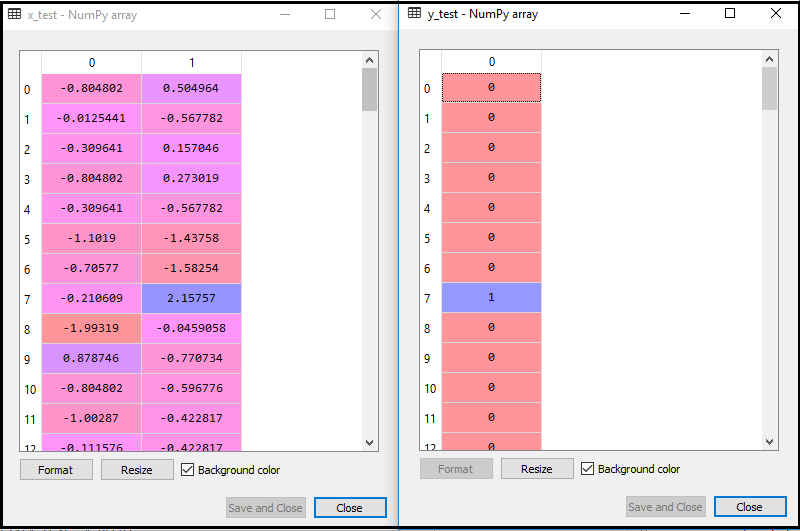
Yllä olevasta tuotoksesta im ikä, voimme nähdä, että tietomme skaalataan onnistuneesti.

• K-NN-luokittelijan sovittaminen harjoitustietoihin:
  Nyt sovitamme K-NN-luokituksen harjoitustietoihin. Tätä varten tuomme Sklearn Neighbors -kirjaston KNeighborsClassifier-luokan. Luokan tuomisen jälkeen luomme luokan Classifier-objektin. Tämän luokan parametri on
  • n_naapurit: Algoritmin vaadittujen naapureiden määrittäminen. Yleensä se vie viisi.
  • metric = ”minkowski”: Tämä on oletusparametri ja se päättää pisteiden välisen etäisyyden.
  • p = 2: Se vastaa standardia Euklidinen metriikka.

  Ja sitten sovitamme luokittelijan harjoitustietoihin. Alla on sen koodi:

Output: Suorittamalla yllä oleva koodi saamme lähdön muodossa:

• Testituloksen ennustaminen: Testijoukon tuloksen ennustamiseksi luomme y_pred-vektorin, kuten teimme logistisessa regressiossa. Alla on sen koodi:

Tulos:

Yllä olevan koodin lähtö on:

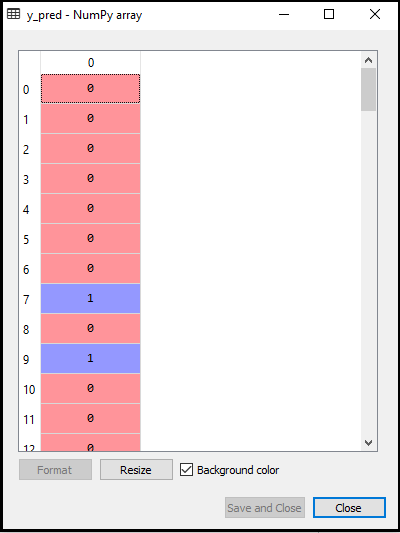
• Sekaannusmatriisin luominen:
  Luomme nyt sekaannusmatriisin K-NN-mallillemme nähdäksemme luokittelijan tarkkuuden. Alla on sen koodi:

Yllä olevaan koodiin olemme tuoneet confusion_matrix-funktion ja kutsuneet sitä muuttujalla cm.

Output: Suorittamalla yllä oleva koodi saadaan matriisi kuten alla:

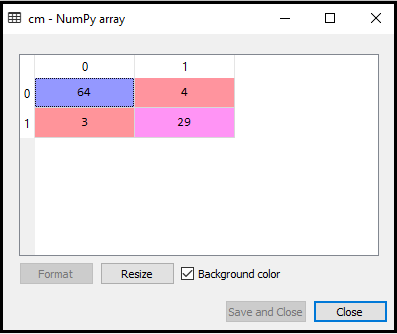
Yllä olevassa kuvassa näemme on 64 + 29 = 93 oikeaa ennustetta ja 3 + 4 = 7 väärää ennustetta, kun taas logistisessa regressiossa oli 11 väärää ennustetta. Joten voimme sanoa, että mallin suorituskykyä parannetaan käyttämällä K-NN-algoritmia.

• Harjoittelujoukon tuloksen visualisointi:
  Nyt visualisoimme K-harjoitussarjan tuloksen -NN-malli. Koodi pysyy samana kuin teimme logistisessa regressiossa, paitsi kaavion nimi. Alla on sen koodi:

Tulos:

Suorittamalla yllä oleva koodi saadaan alla oleva kaavio:

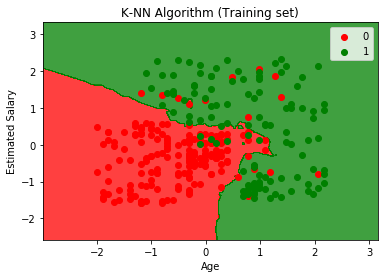
Lähtökaavio eroaa kaaviosta, jonka olemme havainneet logistisessa regressiossa. Se voidaan ymmärtää seuraavista kohdista:

• Kuten voimme nähdä, kaavio näyttää punaisen ja vihreän pisteen. Vihreät pisteet koskevat muuttujaa Ostettu (1) ja Punaisia pisteitä ostamattomista (0).
• Kaavio näyttää epäsäännöllisen rajan suoran tai minkä tahansa käyrän sijasta, koska se on K-NN-algoritmi, toisin sanoen lähimmän naapurin löytäminen.
• Kaaviossa on luokiteltu käyttäjät oikeisiin luokkiin, koska suurin osa käyttäjistä, jotka eivät ostaneet maastoautoa, ovat punaisella alueella ja käyttäjät, jotka ostivat maastoauton, ovat vihreällä alueella.
• Kaavio näyttää hyvän tuloksen, mutta silti punaisella alueella on joitain vihreitä pisteitä ja vihreällä alueella. Mutta tämä ei ole iso ongelma, koska tekemällä tämä malli estetään yliasennuskysymykset.
• Siksi mallimme on hyvin koulutettu.
• Testisarjan tuloksen visualisointi:
  Mallin harjoittelun jälkeen testaamme tuloksen asettamalla uuden tietojoukon eli Testitietojoukko. Koodi pysyy samana lukuun ottamatta joitain pieniä muutoksia: kuten x_train ja y_train korvataan x_test ja y_test.
  Alla on sen koodi:

Tulos:

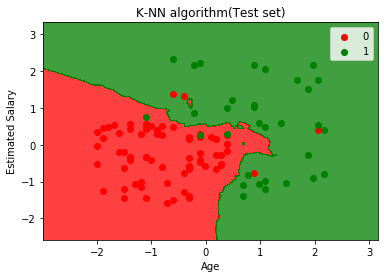
Yllä oleva kaavio näyttää testidatan tuotoksen. Kuten kaaviosta voidaan nähdä, ennustettu tulos on hyvin hyvä, koska suurin osa punaisista pisteistä on punaisella alueella ja suurin osa vihreistä pisteistä on vihreällä alueella.

Punaisella alueella on kuitenkin vähän vihreitä pisteitä ja vihreällä alueella muutama punainen. Joten nämä ovat virheellisiä havaintoja, jotka olemme havainneet sekaannusmatriisissa (7 väärä tulos).