Mäkeen jyrkkyyttä kutsutaan kaltevuudeksi. Sama koskee linjan jyrkkyyttä. Kaltevuus määritellään kahden pisteen, nousun, pystysuoran muutoksen ja nousun suhteeksi kahden saman pisteen, juoksun, vaakamuutokseen.

$$ slope = \ frac {nousu} {juoksu} = \ frac {change \: in \: y} {change \: in \: x} $$

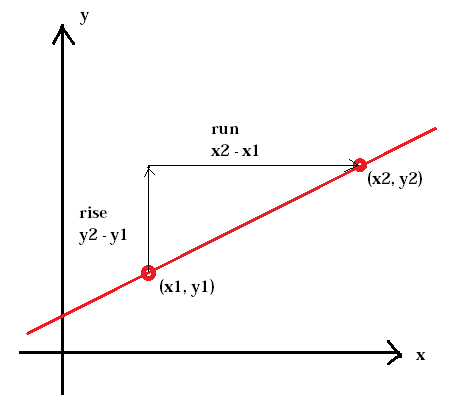
viivan kaltevuutta edustaa yleensä kirjain m. (x1, y1) edustaa ensimmäistä pistettä, kun taas (x2, y2) edustaa toista pistettä.

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2 } \, -x_ {1}} $$

On tärkeää, että x- ja y-koordinaatit pidetään samassa järjestyksessä sekä osoittajassa että nimittäjässä, muuten saat väärän kaltevuuden.

Esimerkki

Etsi viivan kaltevuus

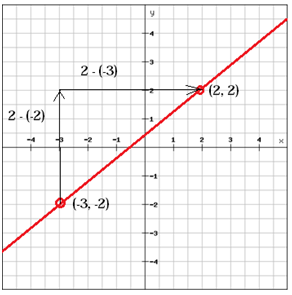
(x1, y1 ) = (-3, -2) ja (x2, y2) = (2, 2)

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ { 2} \, -x_ {1}} = \ frac {2- \ vasen (-2 \ oikea)} {2- \ vasen (-3 \ oikea)} = \ frac {2 + 2} {2 + 3} = \ frac {4} {5} $$

Viiva, jolla on positiivinen kaltevuus (m > 0), kun yllä oleva viiva nousee vasemmalta oikealle, kun taas negatiivisen kaltevuuden viiva (m < 0) putoaa vasemmalta oikealle.

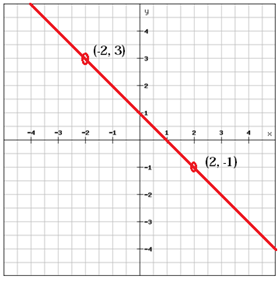
$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2} \, -x_ {1}} = \ frac {\ vasen (-1 \ oikea) -3} {2- \ vasen (-2 \ oikea)} = \ frac {-1-3} {2 + 2} = \ frac {-4} {4} = – 1 $$

Jos kahdella viivalla on sama kaltevuus, linjojen sanotaan olevan p rinnakkainen.

Voit ilmaista lineaarisen funktion käyttämällä kaltevuuden sieppauslomaketta.

$$ y = mx + b $$

$$ m = kaltevuus $ $

$$ b = y – siepata $$

Videotunti

Etsi kaltevuus