MATH 1314: College Algebra (Suomi)
Vaikka pystysuorat asymptootit kuvaavat kuvaajan käyttäytymistä, kun ulostulo saa hyvin suuren tai hyvin pienen, vaakasuuntaiset oireet auttavat kuvaamaan kuvaajan käyttäytymistä panos on hyvin suuri tai hyvin pieni. Muistakaa, että polynomin loppukäyttäytyminen heijastaa päätermin käyttäytymistä. Samoin järkevä funktion loppukäyttäytyminen heijastaa osoittaja- ja nimittäjäfunktioiden etusuhteiden suhdetta.
Vaakasuuntaisten asymptoottien tarkistuksessa on kolme erillistä tulosta:
Tapaus 1: Jos nimittäjän aste > osoittajan aste, y = 0: lla on vaakasuora asymptootti.

Tapaus 2: Jos nimittäjän aste < osoittajan aste yhdellä, saamme vinon asymptootin.

Huomaa, että vaikka rationaalisen funktion kaavio ei koskaan ylitä pystysuoraa asymptoottia, kaavio voi tai ei saa ylittää vaakasuoraa tai vinoa ymptote. Lisäksi, vaikka rationaalisen funktion kaaviossa voi olla monia pystysuoria asymptooteja, kaaviossa on enintään yksi vaakasuora (tai vino) asymptootti.
On huomattava, että jos osoittajan aste on suurempi kuin nimittäjän aste useammalla kuin yhdellä, kaavion loppukäyttäytyminen jäljittelee pienennetyn loppukäyttäytymisfraktion käyttäytymistä. Jos meillä olisi esimerkiksi toiminto
loppukäyttäytymisellä
kaavion loppukäyttäytyminen näyttäisi samanlaiselta kuin tasaisen polynomin, jolla on positiivinen johtava kerroin.
Yleinen huomautus: Rationaalisten toimintojen vaakasuorat oireet
Rationaalisen funktion vaakasuora asymptootti voi olla määritetään katsomalla osoittajan ja nimittäjän astetta.
- Osoittimen aste on pienempi kuin nimittäjän aste: vaakasuora asymptootti y = 0.
- Osoittimen aste on suurempi kuin nimittäjän aste yhdellä: ei vaakasuoraa asymptoottia; vino asymptootti.
- Osoittimen aste on sama kuin nimittäjän aste: vaakasuora asymptootti johtavien kertoimien suhteen.
Esimerkki 9: Vaaka- ja pystysuuntaisten oireiden tunnistaminen
Etsi funktion vaaka- ja pystysuuntaiset asymptootit
Ratkaisu
Huomaa ensin, että tällä toiminnolla ei ole yhteisiä tekijöitä, joten ei ole potentiaalisia irrotettavia epäjatkuvuuksia.
Toiminnolla on pystysuorat asymptootit, kun nimittäjä on nolla, mikä aiheuttaa funktion määrittelemättömyyden. Nimittäjä on nolla kohdassa x = 1, -2, teksti {ja} 5 \, mikä osoittaa pystysuorat asymptootit näissä arvoissa.
Osoittimessa on aste 2, kun taas nimittäjässä aste 3. Asteesta lähtien. nimittäjän arvo on suurempi kuin osoittajan aste, nimittäjä kasvaa nopeammin kuin osoittaja, jolloin lähdöt pyrkivät kohti nollaa, kun tulot kasvavat, ja niin kuin xto pm infty, lentänyt (xoikea) arvoon 0 \. Tällä toiminnolla on vaakasuora asymptootti kohdassa y = 0 \.
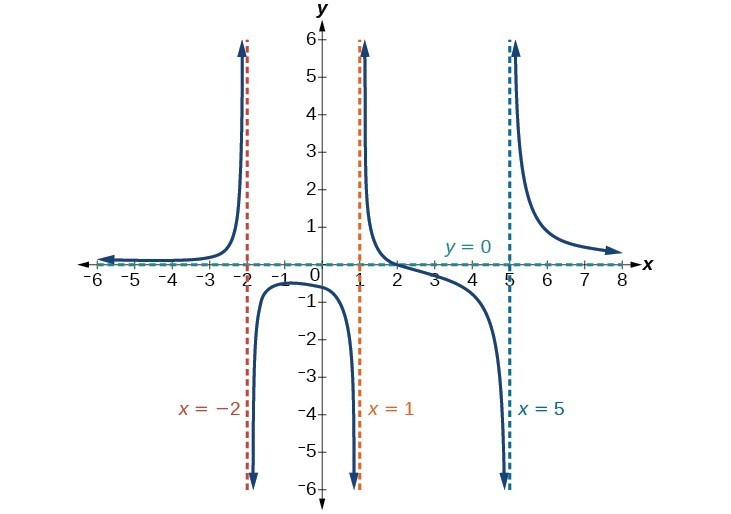
Kuva 15
Yleinen huomautus: Rationaalisten toimintojen sieppaukset
Rationaalisella funktiolla on y-leikkaus, kun tulo on nolla, jos funktio on määritelty nollaksi. Rationaalisella funktiolla ei ole y-leikkausta, jos funktiota ei ole määritelty nollassa.
Samoin järkevällä funktiolla on x-sieppauksia tuloissa, jotka aiheuttavat lähdön nollan. Koska murtoluku on vain yhtä suuri kuin nolla, kun osoittaja on nolla, x-sieppauksia voi esiintyä vain, kun järkevän funktion osoittaja on nolla.
Kokeile 7
Kun otetaan huomioon vastavuoroinen neliöfunktio, joka on siirretty oikealle 3 yksikköä ja alaspäin 4 yksikköä, kirjoita tämä järkeväksi funktioksi. Etsi sitten x- ja y-sieppaukset sekä vaaka- ja pystysuuntaiset asymptootit.
Ratkaisu