Ratkaisut
ColligativeProperties
Höyrynpaineen aleneminen
Fysikaaliset ominaisuudet voidaan jakaa kahteen luokkaan. Laajat ominaisuudet (kuten massa ja tilavuus) riippuvat näytteen koosta. Intensiiviset ominaisuudet (kuten tiheys ja konsentraatio) ovat aineelle tyypillisiä ominaisuuksia; ne eivät riipu tutkittavan näytteen koosta. Thissection esittelee kolmannen luokan, joka on järjestelmän intensiivisten ominaisuuksien osajoukko. Tätä kolmatta luokkaa, joka tunnetaan kollektiivisina kiinteistöinä, voidaan soveltaa vain ratkaisuihin. Bydefinition, yksi liuoksen ominaisuuksista on kolligatiivinen omaisuus, jos se riippuu vain liuenneen aineen ja liuottimen hiukkasten lukumäärästä, ei liuenneen aineen identiteetistä.
Hyvin harvat ratkaisun fysikaalisista ominaisuuksista ovat yhdistäviä ominaisuuksia. Esimerkkinä tästä rajoitetusta fysikaalisten ominaisuuksien joukosta tarkastellaan mitä tapahtuu liuottimen höyrynpaineelle, kun lisätään liuotinta liuoksen muodostamiseksi. Määritämme Po: n puhtaan nesteen höyrynpaineeksi ![]() liuotin
liuotin ![]() ja P liuottimen höyrynpaineena liuenneen aineen lisäämisen jälkeen.
ja P liuottimen höyrynpaineena liuenneen aineen lisäämisen jälkeen.
Po = puhtaan nesteen tai liuottimen höyrynpaine
P = liuottimen höyrynpaine liuoksessa
Kun nesteen lämpötila on sen kiehumisen alapuolella voidaan olettaa, että ainoat molekyylit, jotka voivat paeta nestemäisestä aineesta kaasun muodostamiseksi, ovat ne, jotka ovat lähellä nestemäisen pinnan pintaa.
Kun liuotinta lisätään liuottimeen, jotkut solutemolekyylit vievät nesteen pinnan lähellä olevan tilan, kuten alla olevassa kuvassa esitetään. Kun liuenneen aine liuotetaan liuottimeen, liuottimen molekyylien määrä lähellä pintaa pienenee ja liuottimen höyrynpaine laskee.

Tällä ei ole vaikutusta nopeuteen, jolla liuotinmolekyylit kaasufaasissa kondensoituvat muodostaen nesteen. Mutta se pienenee, kun nesteen liuotinmolekyylit pääsevät pakenemaan kaasufaasista. Tämän seurauksena liuoksesta poistuvan liuottimen höyrynpaineen tulisi olla pienempi kuin puhtaan liuottimen höyrynpaine.
| P | < | Po | ||
| höyrynpaine | liuotin liuoksen yläpuolella |
puhtaan liuottimen höyrynpaine |
Vuosien 1887 ja 1888 välillä Francois-Marie Raoult osoitti, että liuoksen höyrynpaine on yhtä suuri kuin liuottimen mooliosuus kertaa puhtaan nesteen höyrynpaine.
| P | = | Csolvent Po | ||||
| höyrynpaine liuotinta liuoksen yläpuolella |
puhtaan liuottimen höyrynpaine |
Tämä yhtälö, joka tunnetaan nimellä Raoultin laki, on helppo ymmärtää. Kun liuotin on puhdas ja liuottimen molefraktio on 1, P on yhtä suuri kuin Po.Kun liuottimen mooliosuus pienenee , liuoksesta poistuvan liuottimen höyrynpaine tulee myös pienemmäksi. Oletetaan toistaiseksi, että liuotin on ainoa komponentti liuoksesta, joka on riittävän haihtuva, jotta sillä olisi mitattavissa oleva höyrynpaine. Jos tämä on totta, liuoksen höyrynpaine on yhtä suuri kuin liuoksesta poistuvan liuottimen höyrynpaine. Raoultin lain mukaan puhtaan liuottimen höyrynpaineen ja liuoksen välinen ero kasvaa, kun liuottimen mooliosuus pienenee.
Höyrynpaineen muutos, joka tapahtuu, kun liuotteeseen lisätään liuotinta, Siksi kolligatiivinen ominaisuus. jos se riippuu liuenneen aineen mooliosuudesta, sen on oltava riippuvainen liuenneen aineen tososaa liuenneesta aineesta olevien hiukkasten lukumäärästä, mutta ei liuenneen aineen identiteetistä.
![]()
Kiehumispisteen nousu ja jäätymispisteen aleneminen
Alla olevassa kuvassa esitetään seuraukset siitä, että liuotin alentaa höyrynpainetta. tämän vaihekaavion linjaliitäntäpisteet B ja C sisältävät lämpötilan ja paineen yhdistelmät, joissa puhdas liuotin ja sen höyry ovat tasapainossa. Tämän johdon kukin piste kuvaa siis liuottimen höyrynpaineen kyseisessä lämpötilassa. Tämän kuvion katkoviiva kuvaa oikean liuosta, joka on saatu liuottamalla asoluutti liuottimeen.Missä tahansa lämpötilassa liuoksesta poistuvan liuottimen höyrynpaine on pienempi kuin puhtaan liuottimen höyrynpaine. Pisteviiva on siksi kiinteän viivan alapuolella.
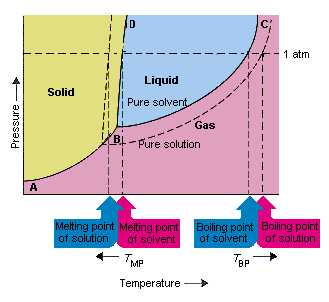
liuottimen höyrynpaine, joka tapahtuu, kun liuotinta lisätään liuottimeen, aiheuttaa kiehumispisteen nousun ja laskun liuoksen sulamispisteessä.
Tämän kuvan mukaan liuos ei voi kiehua samassa lämpötilassa puhtaana liuottimena. Jos höyrynpaine on liuoksesta poistuva liuotin on pienempi kuin puhtaan liuottimen höyrynpaine tietyssä lämpötilassa, liuos on kuumennettava korkeammaan lämpötilaan ennen kuin se kiehuu. Liuottimen höyrynpaineen aleneminen, kun sitä käytetään liuoksen muodostamiseen nostaa nesteen kiehumispistettä.
Kun vaihekaaviot otettiin käyttöön, kolmoispiste määriteltiin ainoaksi lämpötilan ja paineen yhdistelmäksi, jossa kaasu, neste ja kiinteä aine voivat olla samanaikaisesti. Yllä oleva kuva osoittaa että liuoksen kolminkertainen piste tapahtuu alemmassa lämpötilassa kuin puhtaan liuottimen kolminkertainen piste. Itse asiassa kolmoispisteen muutos ei ole tärkeä, mutta se johtaa lämpötilan muutokseen, jossa liuos jäätyy tai sulaa. miksi, meidän on etsittävä hoitoa täysin linjalla, joka erottaa kiinteät ja nestemäiset alueet faasiarvossa. Tämä viiva on melkein pystysuora, koska aineen sulamispiste ei ole kovin herkkä paineelle.
Tämän linjan on kuitenkin kuljettava liuoksen kolmoiskohdan läpi. Kolmoiskohdan lasku, joka tapahtuu, kun liuotin liuotetaan liuokseen, vähentää siten liuoksen sulamispistettä.
Yllä oleva kuva osoittaa, kuinka höyrynpaineen muutos, joka tapahtuu liuenneen aineen liuottessa liuottimeen, johtaa muutoksiin myös sulamispisteessä ja liuottimen kiehumispisteessä. , liuottimen kiehumispisteen ja sulamispisteen muutokset ovat myös kolligatiivisia ominaisuuksia.
![]()
ColligativeProperties-laskelmat
Paras tapa demoneihin kollektiivisten omaisuuksien merkitys on tutkia Raoultin lain seurauksia. Havaittiin, että liuoksesta poistuvan liuottimen höyrynpaine on verrannollinen liuottimen mooliosaan.
P = CsolventPo
Mutta liuottimen höyrynpaine ei ole kolligatiivista omaisuutta. Ainoastaan höyrynpaineen muutos, joka tapahtuu, kun liuotinta lisätään liuottimeen, voidaan sisällyttää liuoksen kolligatiivisiin ominaisuuksiin.
Koska paine on tilatoiminto, muutos liuottimen höyrynpaineessa, joka tapahtuu, kun liuotinta lisätään liuottimeen, voidaan määritellä erona puhtaan liuottimen höyrynpaineen ja liuottimen höyrynpaineen välillä. paeta ratkaisusta.
P = Po – P
Raoultin lain korvaaminen tähän yhtälöön antaa seuraavan tuloksen.
P = Po – Csolvent Po = (1 – Csolvent) Po
Tätä yhtälöä voidaan yksinkertaistaa muistamalla terolaation liuenneen aineen mooliosuuden ja liuottimen molefraktion välillä.
Csolute + Csolvent = 1
Korvaa tämä suhde yhtälöön, joka määrittelee Pgivesin toisen muodon Raoultin laista.
P = CsolutePo
Tämä yhtälö muistuttaa meitä siitä, että liuottimen höyrynpaineen muutos, joka tapahtuu, kun liuotinta lisätään liuoteaineeseen, on verrannollinen liuenneen aineen mooliosaan. Kun moresoluutti liuotetaan liuottimeen, liuottimen höyrynpaine pienenee ja liuottimen höyrynpaineen muutos kasvaa.
Koska liuottimen kiehumispisteen (TBP) muutokset, jotka tapahtuvat, kun liuotinta lisätään liuottimeen, johtuvat liuottimen höyrynpaineen muutoksista, kiehumispisteen muutoksen suuruus on myös verrannollinen liuenneen aineen molefraktioon.
![]() TBP = kbsolute
TBP = kbsolute
Laimennetuissa liuoksissa liuenneen aineosan mooliosuus on verrannollinen liuoksen molaalisuuteen, kuten alla oleva kuva.

Yhtälö, joka kuvaa kiehumispisteen nousun suuruutta, joka tapahtuu, kun liuoteainetta lisätään liuottimeen, kirjoitetaan siksi usein seuraavasti.
![]() TBP = kbm
TBP = kbm
Täällä ![]() TBP on kiehumispisteen korkeus – kiehumispisteen muutos, joka tapahtuu, kun liukeneva aine liukenee liuottimeen
TBP on kiehumispisteen korkeus – kiehumispisteen muutos, joka tapahtuu, kun liukeneva aine liukenee liuottimeen ![]() ja kb on suhteellisuusvakio, joka tunnetaan liuottimen molempana kiehumispisteen korkeusvakiona.
ja kb on suhteellisuusvakio, joka tunnetaan liuottimen molempana kiehumispisteen korkeusvakiona.
Samanlainen yhtälö voidaan kirjoittaa kuvaamaan mitä tapahtuu liuottimen jäätymispisteeseen (tai sulamispisteeseen), kun liuotinta lisätään liuottimeen.
![]() TFP = -kfm
TFP = -kfm
Tässä yhtälössä ![]() TFP on jäätymispiste masennus
TFP on jäätymispiste masennus ![]() jäätymispisteen muutos, joka tapahtuu, kun liuotin liukenee liuottimeen – ja kf on liuottimen molaalisen jäätymispisteen alenemisvakio. Negatiivista merkkiä käytetään tässä yhtälössä osoittamaan, että liuottimen jäätymispiste laskee, kun liuotettua ainetta lisätään.
jäätymispisteen muutos, joka tapahtuu, kun liuotin liukenee liuottimeen – ja kf on liuottimen molaalisen jäätymispisteen alenemisvakio. Negatiivista merkkiä käytetään tässä yhtälössä osoittamaan, että liuottimen jäätymispiste laskee, kun liuotettua ainetta lisätään.
Kf: n ja kbas: n arvot sekä jäätymispisteet ja kiehumispisteet useille puhtaille liuottimille on annettu alla olevissa taulukoissa.
Jäätymispisteen masennuksen vakiot
Kiehumispisteen korkeuden vakiot
Harjoitusongelma 6:
Laske rikin molekyylipaino, jos 35,5 grammaa rikkiä liukenee 100,0 grammaan CS2: ta, jolloin saadaan liuos, jonka kiehumispiste on 49,48oC.
Napsauta tätä tarkistaaksesi vastauksesi harjoitusongelmaan 6
Napsauta tätä nähdäksesi ratkaisun käytännön tehtävään 6
Harjoitusongelma 7:
Määritä etikkahapon molekyylipaino, jos liuos, joka sisältää 30,0 grammaa etikkahappoa per kilogramma vettä jäätyy -0,93oC: ssa. Ovatko nämä tulokset olettamuksen kanssa, jonka mukaan etikkahapolla on kaava CH3CO2H?
Napsauta tätä tarkistaaksesi vastauksesi harjoitusongelmaan 7
Napsauta tätä nähdäksesi ratkaisun käytännön ongelmaan 7
Mitä tapahtuisi käytännön tehtävän 7 laskennassa, toistettiin vahvemmalla hapolla, kuten tuhasuolahapolla?
Harjoitusongelma 8:
Selitä, miksi bentseeniin liuotetulla 0,100 m: n HCl-liuoksella on jäätymispisteen lasku 0,512 ° C, kun taas 0,100 m: n vesiliuoksella on jäätymispisteen lasku 0,352 ° C.
Napsauta tätä tarkistaaksesi vastauksesi harjoitustehtävään 8
Vuonna 1884 Jacobus Henricus van ”t Hoff esitteli toisen termin jäätymispisteen laskuun ja kiehumispisteen korkeusilmaisuihin selittääkseen yhdisteiden liuosten kolligatiivisia ominaisuuksia, jotka hajoavat, kun ne liukenevat veteen.
![]() TFP = – kf (i) m
TFP = – kf (i) m
Korvaamalla koearvo 0,100 m HCl-liuoksen jäätymispistepaineelle tässä yhtälössä saadaan arvo i-aikavälille 1,89. Jos HCl ei irtoaisi vedestä, olisin 1. Jos se dissosioituu kokonaan, olisin 2. Kokeellinen arvo 1,89 viittaa siihen, että vähintään 95% HCl-molekyyleistä dissosioituu tässä ratkaisussa.
Harjoittelu Tehtävä 9:
Selitä, miksi 0,60 grammaa etikkahappoa liukenee 200 grammaan bentseeniä muodostaen liuoksen, joka alentaa bentseenin jäätymispisteen 5,40 ° C: seen.
Tarkista vastaus napsauttamalla tätä Harjoitusongelma 9
![]()
Osmoottinen paine
Vuonna 1784 ranskalainen fyysikko ja pappi Jean AntoineNollet huomasi, että sian virtsarakko, joka oli täytetty väkevällä alkoholiliuoksella vedessä, laajeni, kun se upotettiin veteen. Virtsarakko toimi puoliläpäisevänä kalvona, joka antoi vesimolekyylien päästä liuokseen, mutta estää alkoholimolekyylien liikkumasta toiseen suuntaan. Liuoksen yhden komponentin liikkumista kalvon läpi liuoksen laimentamiseksi kutsutaan osmoosiksi, ja tuotettua painetta kutsutaan osmoottiseksi paineeksi ().
Osmoottinen paine voidaan osoittaa alla olevassa kuvassa esitetyllä laitteella. Puoliläpäisevä kalvo on sidottu ohdakeputken avoimen pään yli. Sitten putki täytetään osittain sokeri- tai alkoholiliuoksella vedessä ja upotetaan vesilasiin. Vesi virtaa putkeen, kunnes vesipatsaassa oleva paine painovoiman vaikutuksesta tasapainottaa theosmoottisen paineen, joka ajaa vettä kalvon läpi.

Vesi virtaa läpi puoliläpäisevä kalvo alkoholiliuoksen laimentamiseksi, kunnes tämän liuoksen pylväälle vetävä painovoima tasapainottaa osmoottisen paineen, joka työntää vettä kalvon läpi.
Samana vuonna, kun Raoult löysi yhteyden liuoksen höyrynpaineen ja puhdasta liuottimen, Jacobus Henricusin, höyrynpaineen välillä van ”t Hoff havaitsi, että laimennetun liuoksen () osmoottinen paine noudatti yhtälöä, joka on analoginen ihanteellisen kaasuyhtälön kanssa.
| |
= | nRT | ||
| V |
Tämä yhtälö viittaa siihen, että osmoottinen paine on muu esimerkki kolligatiivisesta ominaisuudesta, koska tämä paine riippuu liuenneiden hiukkasten lukumäärän suhteesta liuoksen tilavuuteen ![]() n / V
n / V ![]() ei liuenneiden hiukkasten identiteetistä. muistuttaa myös osmoottisen paineen suuruutta, tämän yhtälön mukaan 1,00 M s oluutiossa on osmoottinen paine 22,4 atm 0 ° C: ssa.
ei liuenneiden hiukkasten identiteetistä. muistuttaa myös osmoottisen paineen suuruutta, tämän yhtälön mukaan 1,00 M s oluutiossa on osmoottinen paine 22,4 atm 0 ° C: ssa.

Tämä tarkoittaa, että 1,00 M: n ratkaisun pitäisi pystyä tukemaan 670 tuuman tai lähes 56 jalan pituista vesipatsaaa !
Biologit ja biokemistit käyttävät osmoottisen paineen hyväksi usein eristäessään solun komponentteja. Kun selli lisätään vesiliuokseen, joka sisältää paljon korkeamman ionipitoisuuden kuin solussa oleva neste, vesi poistaa solun virtaamalla solukalvon läpi, kunnes solu kutistuu niin paljon, että kalvo rikkoutuu. Vaihtoehtoisesti, kun solu sijoitetaan liuokseen, jolla on paljon pienempi ionivahvuus, vettä kaadetaan soluun ja solu laajenee, kunnes solukalvo puhkeaa.
![]()