Parametriset ja ei-parametriset testit kahden tai useamman ryhmän vertailemiseksi

Tilastot: Parametriset ja muut kuin parametritestit

Tämä osio kattaa:

• testin valitseminen
• parametriset testit
• ei-parametriset testit

testin valitseminen

Tilastollisen testin valinnan kannalta tärkein kysymys on ”mikä on tutkimuksen päähypoteesi?” Joissakin tapauksissa ei ole hypoteesia; tutkija haluaa vain ”nähdä, mitä siellä on”. Esimerkiksi esiintyvyystutkimuksessa ei ole testattavaa hypoteesia, ja tutkimuksen koko määräytyy sen mukaan, kuinka tarkasti tutkija haluaa määrittää esiintyvyyden. Jos hypoteesia ei ole, ei ole tilastollista testiä. On tärkeää päättää etukäteen, mitkä hypoteesit ovat vahvistavia (ts. Testaa jotakin oletettua suhdetta) ja mitkä ovat tutkivia (mitä tiedot ehdottavat). Mikään yksittäinen tutkimus ei voi tukea koko joukkoa hypoteeseja. Järkevä suunnitelma on rajoittaa vakavasti vahvistavien hypoteesien määrää. Vaikka on perusteltua käyttää tilastollisia testejä tietojen ehdottamiin hypoteeseihin, P-arvoja tulisi käyttää vain ohjeellisina, ja tuloksia tulisi pitää alustavina, kunnes seuraavat tutkimukset vahvistavat. Hyödyllinen opas on käyttää Bonferroni-korjausta, jossa todetaan yksinkertaisesti, että jos testataan n riippumatonta hypoteesia, on käytettävä merkitsevyystasoa 0,05 / n. Jos siis olisi kaksi riippumatonta hypoteesia, tulos julistettaisiin merkittäväksi vain, jos P < 0,025. Huomaa, että koska testit ovat harvoin riippumattomia, tämä on hyvin konservatiivinen menettely eli ts. Tuskin hylkää nullhypoteesia. Tutkijan tulisi sitten kysyä ”ovatko tiedot riippumattomia?” Tätä voi olla vaikea päättää, mutta nyrkkisääntönä saman henkilön tai vastaavien henkilöiden tulokset eivät ole riippumattomia. Siksi ristikkäistutkimuksen tulokset tai tapaustarkastustutkimus, jossa kontrollit sovitettiin tapauksiin iän, sukupuolen ja sosiaalisen luokan mukaan, eivät ole riippumattomia.

• Analyysin tulisi heijastaa suunnittelua , joten yhteensopivan mallin tulisi seurata vastaava analyysi.
• Ajan mitatut tulokset vaativat erityistä huolellisuutta. Yksi yleisimmistä virheistä tilastollisessa analyysissä on käsitellä korreloivia muuttujia ikään kuin ne olisivat
  riippumattomia. Oletetaan esimerkiksi, että tarkastelimme jalkahaavojen hoitoa, jossa joillakin ihmisillä oli haava kummassakin jalassa. Meillä saattaa olla 20 potilasta, joilla on 30 haavaumaa, mutta itsenäisten tietojen määrä on 20, koska yhden ihmisen haavan tilaan voi vaikuttaa henkilön terveydentila ja analyysi, joka haavoja pidettiin itsenäisinä havaintoina virheellisiä. Jos haluat analysoida sekoitettujen parittamattomien ja parittamattomien
  tietojen oikean analyysin, ota yhteyttä tilastoon.

Seuraava kysymys on ”minkä tyyppisiä tietoja mitataan?” Käytetty testi olisi määritettävä tietojen perusteella. Testin valinta sovitetuille tai pariksi liitetyille tiedoille on kuvattu taulukossa 1 ja riippumattomat tiedot taulukossa 2.

Taulukko 1 Tilastollisen testin valinta paritetusta tai sovitetusta havainnosta

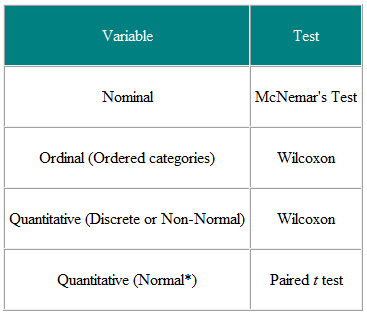
On hyödyllistä päättää syötemuuttujat ja tulosmuuttujat. Esimerkiksi kliinisessä tutkimuksessa panosmuuttuja on hoidon tyyppi – nimellinen muuttuja – ja tulos voi olla jokin kliininen toimenpide ehkä normaalisti jakautunut. Vaadittu testi on t-testi (taulukko 2). Kuitenkin, jos syöttömuuttuja on jatkuva, esimerkiksi kliininen pisteet, ja tulos on nimellinen, sanotaan parantunut tai parantumaton, vaaditaan logistinen regressio. T-testi tässä tapauksessa voi auttaa, mutta ei antaisi meille sitä, mitä tarvitsemme, nimittäin parannuksen todennäköisyyttä tietylle kliinisen pistemäärän arvolle. Toisena esimerkkinä oletetaan, että meillä on poikkileikkaustutkimus, jossa kysytään satunnaisotokselta ihmisiä, luulevatko heidän yleislääkärinsä hyvää työtä viiden pisteen asteikolla, ja haluamme varmistaa, onko naisilla korkeampi mielipide yleislääkärit kuin miehet. Syöttömuuttuja on sukupuoli, joka on nimellinen. Tulosmuuttuja on viiden pisteen järjestysasteikko. Jokaisen henkilön mielipide on riippumaton muista, joten meillä on riippumattomia tietoja. Taulukosta 2 meidän on käytettävä trend2-testiä trendille tai Mann-Whitney U-testiä, jossa on korjaus siteille (Huom. Tasaantuminen tapahtuu, kun kaksi tai useampi arvot ovat samat, joten ei ole tiukasti nousevaa järjestysjärjestystä – missä näin tapahtuu, voidaan keskittää sidottujen arvojen arvot). Huomaa kuitenkin, että jos jotkut ihmiset jakavat yleislääkärin ja toiset eivät, tietoja ei ole riippumattomia ja kehittyneempiä analyyseja vaaditaan. Huomaa, että näitä taulukoita tulisi pitää vain ohjeina, ja jokainen tapaus on tarkasteltava sen ansioiden mukaan.

Taulukko 2 Tilastollisen testin valinta itsenäisille havainnoille

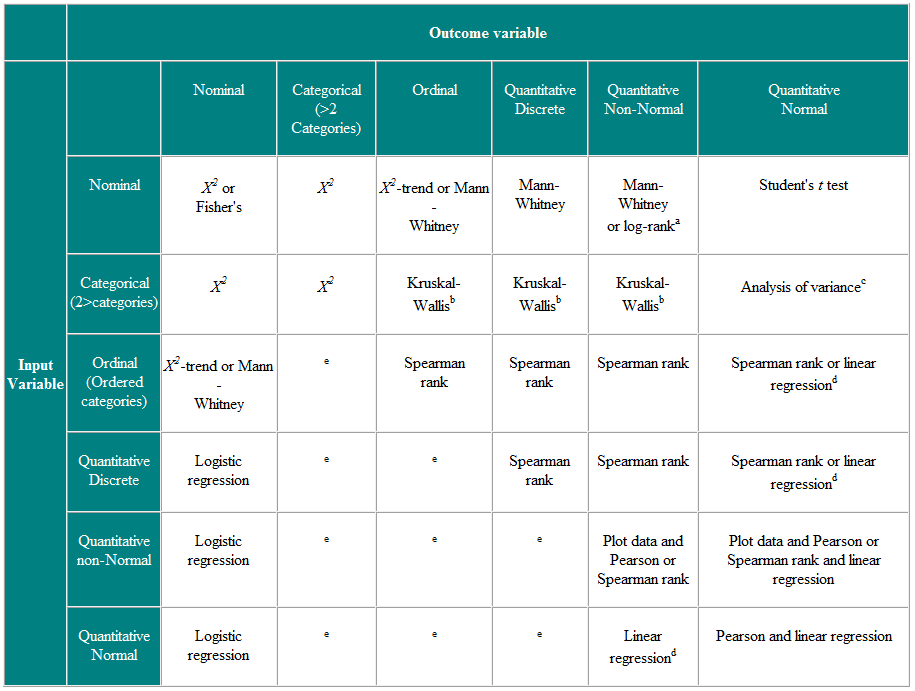
a Jos tietoja sensuroidaan. b Kruskal-Wallisin testiä käytetään vertailemaan järjestysmuuttujia tai ei-normaaleja muuttujia useammalle kuin kahdelle ryhmälle, ja se on yleistys Mann-Whitney U -testille. c Varianssianalyysi on yleinen tekniikka, ja yhtä versiota (yksisuuntainen varianssianalyysi) käytetään vertaamaan normaalijakautuneita muuttujia useammalle kuin kahdelle ryhmälle, ja se on Kruskal-Wallistestin parametrinen vastine. d Jos tulosmuuttuja on riippuvainen muuttuja, edellyttäen, että jäännökset (havaittujen arvojen ja regressiosta ennustettujen vasteiden erot) jakautuvat uskottavasti normaalisti, riippumattoman muuttujan jakauma ei ole tärkeä. e Näissä tilanteissa on useita kehittyneempiä tekniikoita, kuten Poissonin regressio. Ne edellyttävät kuitenkin tiettyjä oletuksia, ja usein on helpompaa joko jakaa tulosmuuttuja tai kohdella sitä jatkuvana.

Parametriset testit tekevät oletuksia populaation jakauman parametreista, joista näyte on otettu. . Tämä on usein oletus, että populaatiotiedot jaetaan normaalisti. Ei-parametriset testit ovat ”jakeluettomia” ja niitä voidaan sellaisenaan käyttää ei-normaaleille muuttujille. Taulukossa 3 on esitetty useiden parametristen testien ei-parametrinen vastine.

Taulukko 3 Parametriset ja Ei-parametriset testit kahden tai useamman ryhmän vertailemiseksi

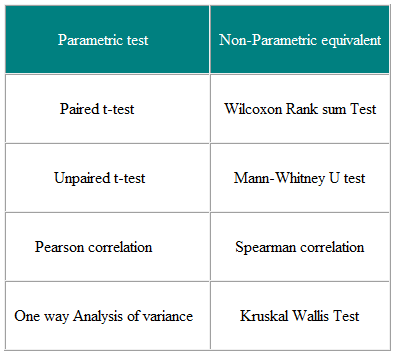
Ei-parametriset testit pätevät sekä ei-normaalisti hajautettuun dataan että Normaalisti jaettu data, joten miksi et käyttäisi niitä koko ajan?

Vaikuttaa järkevältä käyttää kaikissa tapauksissa ei-parametrisia testejä, mikä säästää normaalin testaamisen vaivaa. Parametriset testit ovat suositeltavia, kuitenkin seuraavista syistä:

1. Olemme vain harvoin kiinnostuneita pelkästään merkitsevyystesteistä; haluaisimme sanoa jotain populaatiosta, josta näytteet tulivat, ja tämä voidaan tehdä parhaiten
estimaatit parametreistä ja luottamusvälistä.

2. On vaikea tehdä joustavaa mallinnusta ei-parametrisilla testeillä, esimerkiksi sallimalla sekoittavia tekijöitä käyttämällä useita regressio.

3. Parametrisillä testeillä on yleensä enemmän tilastollista voimaa kuin niiden ei-parametrisilla vastaavilla. Toisin sanoen, todennäköisemmin havaitaan merkittäviä eroja, kun ne ovat todella olemassa.

Vertaavatko muut kuin parametriset testit mediaaneja?

Yleisesti uskotaan, että Mann-Whitney U -testi on itse asiassa testi mediaaniarvoille. Kahdella ryhmällä voi kuitenkin olla sama mediaani ja silti merkittävä Mann-Whitney U -testi. Harkitse seuraavia tietoja kahdesta ryhmästä, joista jokaisella on 100 havaintoa. Ryhmä 1: 98 (0), 1, 2; Ryhmä 2: 51 (0), 1, 48 (2). Mediaani on molemmissa tapauksissa 0, mutta Mann-Whitney-testistä P < 0,0001. Vain jos olemme valmiita tekemään lisäoletuksen siitä, että kahden ryhmän ero on yksinkertaisesti sijainnin muutos (toisin sanoen tietojen jakautuminen yhteen ryhmään yksinkertaisesti siirtyy kiinteällä määrällä toisesta), voimme sanoa, että testi on testi mediaanien erosta. Jos ryhmillä on kuitenkin sama jakauma, sijainnin muutos siirtää mediaaneja ja keinoja samalla määrällä, joten mediaanien ero on sama kuin keskiarvojen ero. Täten Mann-Whitney U -testi on myös testi keskiarvoille. Kuinka Mann-Whitney U -testi liittyy t-testiin? Jos syötettäisiin tietojen rivit eikä itse tiedot kahteen näyte-t-testiohjelmaan, saatu P-arvo olisi hyvin lähellä Mann-Whitney U -testin tuottamaa arvoa.