Voimalaskelmat

Voima työntää tai vedä.
Kohteen voimat ovat yleensä tasapainossa (jos epätasapainoinen objekti kiihtyy):
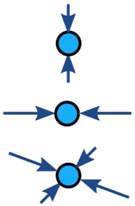 |
 |
|
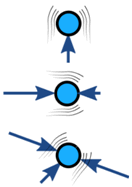
| tasapainossa | epätasapainoinen | |
|---|---|---|
| Ei kiihtyvyyttä | Kiihtyvyys |
Esimerkki: Tämän sillan tornin yläosassa olevat voimat ovat tasapainossa (se ei kiihdy):

Kaapelit vetävät alaspäin yhtä paljon vasemmalle ja oikealle, ja sitä tasapainottaa tornin ylöspäin suuntautuva työntö. (Torni työntyy? Kyllä! Kuvittele, että seisot siellä tornin sijasta.)
Voimme mallintaa voimat näin:

Ja kun laita ne päähänsä häneen, näemme heidän sulkeutuvan takaisin itseensä, eli nettovaikutus on nolla:

Voimat ovat tasapainossa.
Tasapainossa olevien voimien sanotaan olevan tasapainossa: liikkeessä ei myöskään ole muutoksia.
Vapaa kehon kaavio
Ensimmäinen askel on piirtää vapaa vartalokaavio (jota kutsutaan myös voimakuvaksi)
Vapaa vartalokaavio: luonnos, jossa ruumis on irrotettu maailmasta lukuun ottamatta siihen vaikuttavia voimia.
Siltaesimerkissä tornin yläosan vapaa runkokaavio on:

Ilmainen runkokaavio
Se auttaa ajattelemme selkeästi kehoon vaikuttavia voimia.
Esimerkki: Auto valtatiellä
Mitkä ovat moottoritiellä risteilevän auton voimat?

Moottori toimii ahkerasti, joten miksi auto ei kiihdy edelleen?
Koska ajo voimaa tasapainottaa:
- Ilmanvastus (yksinkertaisesti sanottuna: th e ilma vastustaa sitä, että sitä työnnetään ympäriinsä),
- vierintävastus, jota kutsutaan myös vierintäkitkaksi (renkaiden muoto muuttuu)

Ilmainen runkokaavio
W on auton paino,
R1 ja R2 ovat renkaiden vierintävastus,
N1 ja N2 ovat reaktiovoimia (tasapainottavat auton painoa).
Huomaa: Teräspyörillä (kuten junissa) on vähemmän vierintävastusta, mutta ne ovat aivan liian liukkaita tiellä!
Laskelmat
Voima on vektori. Vektorilla on suuruus (koko) ja suunta:

Voimme mallintaa voimat piirtämällä oikean kokoisia ja suuntaisia nuolia . Näin:
Esimerkki: Näkymän ihailu
Brady seisoo parvekkeen reunalla, jota tukee vaakasuora palkki ja tukijalka:

Hän painaa 80 kg.
Mitkä ovat voimat?
Otetaan paikka, jossa hän seisoo, ja ajattele juuri siellä olevia voimia:

Hänen painonsa
Hänen 80 kg: n massa aiheuttaa painovoiman vuoksi alaspäin suuntautuvan voiman.
Voima on massa kertaa kiihtyvyys: F = ma
Maapallon painovoiman aiheuttama kiihtyvyys on 9,81 m / s2 , joten a = 9,81 m / s2
F = 80 kg × 9,81 m / s2
F = 785 N
Muut voimat
Voimat ovat tasapainossa, joten niiden tulisi sulkea itsensä näin:

Voimme käyttää trigonometriaa sen ratkaisemiseksi .
Koska se on suorakulmainen kolmio, SOHCAHTOA auttaa.
Säteessä tunnemme vierekkäiset, haluamme tietää vastakohdat ja ”TOA” kehottaa meitä käyttämään tangenttia:
ruskea (60 ° ) = Palkki / 785 N
Palkki / 785 N = ruskea (60 °)
Palkki = ruskea (60 °) × 785 N
Palkki = 1.732 … × 785 N = 1360 N
Jousijalan kohdalla tunnemme vierekkäiset, haluamme tuntea hypotenuusen, ja ”CAH” kehottaa meitä käyttämään kosinia:
cos (60 °) = 785 N / Strut
Strut × cos (60 °) = 785 N
Strut = 785 N / cos (60 °)
Strut = 785 N / 0,5 = 1570 N
Ratkaistu:

Kiinnostavaa kuinka paljon voimaa on palkki ja tukijalka verrattuna tuettavaan painoon!
Vääntömomentti (tai momentti)
Entä jos palkki on vain kiinni seinässä (kutsutaan konsoliksi)?

Tukijalkaa ei ole, joten mitä voimille tapahtuu?
Vapaa kehon kaavio näyttää tältä:

Ylöspäin suuntautuva voima R tasapainottaa alaspäin suuntautuvaa painoa.
Vain näillä kahdella voimat palkki pyörii kuin potkuri! Mutta on myös ”kääntyvä vaikutus” M, jota kutsutaan hetkeksi (tai momentiksi) ja joka tasapainottaa sen:
Moment: Voima kertoo etäisyyden suorassa kulmassa.
Tiedämme, että paino on 785 N, ja meidän on myös tiedettävä etäisyys suorassa kulmassa, joka tässä tapauksessa on 3,2 m.
M = 785 N x 3,2 m = 2512 Nm
Ja se hetki on se, mikä estää säteen pyörimisen.

Voit tuntea hetken tarttuessasi ongeen.
Sen lisäksi, että pidät painosi yllä, sinun on estettävä sen pyöriminen alaspäin.
Kitka
ramppi rampilla
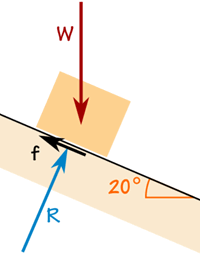
Laatikko painaa 100 kg.
Kitkavoima riittää pitämään sen missä se on.
Reaktiovoima R on suorassa kulmassa ramppi.
Laatikko ei kiihdy, joten voimat ovat tasapainossa:
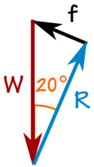
100 kg massa luo painovoiman vuoksi alaspäin suuntautuvan voiman:
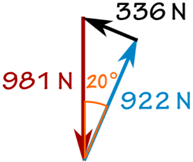
W = 100 kg × 9,81 m / s2 = 981 N
Voimme käyttää SOHCAHTOA: ta kolmion ratkaisemiseen.
Kitka f:
sin (20 °) = f / 981 N
f = sin (20 °) × 981 N = 336 N
Reaktio N:
cos (20 °) = R / 981 N
R = cos (20 °) × 981 N = 922 N
Ja saamme:
Vinkkejä vapaiden vartalokaavioiden piirtämiseen
- Piirrä mahdollisimman yksinkertaisesti. Laatikko on usein tarpeeksi hyvä.
- Voimat osoittavat kehoon vaikuttavaan suuntaan
- suorat nuolet voimia varten
- kaarevat nuolet hetkeksi
Sam ja Alex vetävät laatikkoa
Laskelmat voivat joskus olla helpompia, kun muutamme suuruuden ja suunnan x: ksi ja y: ksi:
 |
< = > |  |
| Vektori a Polar-koordinaateissa | Vektori a karteesisella koordinaatit |
Voit lukea niiden muuntamisen Polar- ja Cartesian-alueilla Koordinaatit, mutta tässä on lyhyt yhteenveto:
Käytetään niitä!