Le Central Limit Theorem nous dit qu’à mesure que la taille des échantillons augmente, la distribution d’échantillonnage de la moyenne deviendra normalement distribuée, même si les données de chaque échantillon ne sont pas normalement distribuées.

Nous pouvons le voir dans des données réelles. Travaillons avec la variable AlcoholYear dans la distribution NHANES, qui est fortement asymétrique, comme indiqué dans le panneau de gauche de la figure ??. Cette distribution est, faute d’un meilleur mot, funky – et certainement pas normalement distribuée. Examinons maintenant la distribution d’échantillonnage de la moyenne de cette variable. La figure 12.2 montre la distribution d’échantillonnage pour cette variable, qui est obtenue en tirant à plusieurs reprises des échantillons de taille 50 à partir de l’ensemble de données NHANES et en prenant la moyenne. Malgré la non-normalité évidente des données d’origine, la distribution d’échantillonnage est remarquablement proche de la normale.

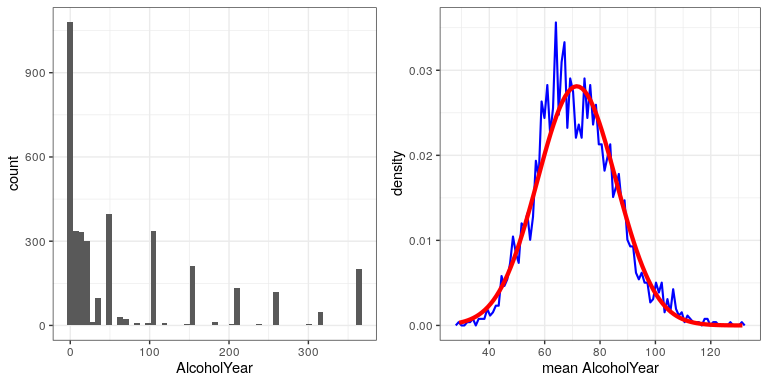
Le théorème central des limites est important pour les statistiques car il nous permet de supposer en toute sécurité la distribution d’échantillonnage de la moyenne sera normale dans la plupart des cas. Cela signifie que nous pouvons tirer parti des techniques statistiques qui supposent une distribution normale, comme nous le verrons dans la section suivante.