Lorsque vous lancez un projectile à un angle # theta # par rapport à l’horizontale, la vitesse initiale du projectile sera ont une composante verticale et une composante horizontale.

# {(v_ (0x) = v_0 * cos (theta)), (v_ (0y) = v_0 * sin (theta)):} #

Afin de déterminer la hauteur maximale atteinte par le projectile pendant son vol, vous devez regarder la composante verticale de son mouvement.

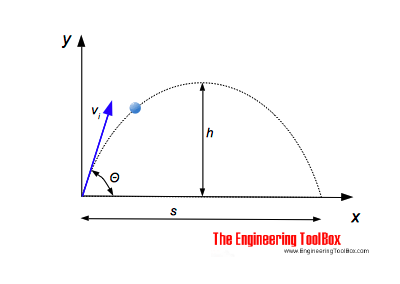
Verticalement, le mouvement du projectile est affecté par la gravité. Cela signifie qu’à hauteur maximale, la composante verticale de la vitesse initiale sera nulle.

Le projectile décélérera sur son chemin vers la hauteur maximale, s’arrêtera complètement à la hauteur maximale, puis commencera sa chute libre descente vers le sol.

Si vous utilisez la composante verticale de sa vitesse initiale, vous pouvez écrire

#underbrace (v_ « h max » ^ 2) _ (color (blue) (« = 0 » )) = v_text (0y) ^ 2 – 2 * g * h_ « max » #

Ceci est équivalent à

#v_ (0y) ^ 2 = 2 * g * h_ « max » #

La hauteur maximale atteinte par le projectile sera donc

#h_ « max » = v_ (0y) ^ 2 / (2 * g) = (v_0 * sin (thêta)) ^ 2 / (2 * g) #

#h_ « max » = couleur (vert) ((v_0 ^ 2 * sin ^ 2 (thêta)) / (2 * g) ) #