Forcer les calculs

La force consiste à pousser ou à tirer.
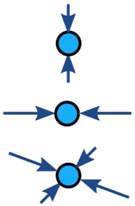
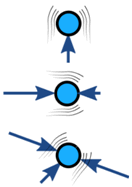
Les forces sur un objet sont généralement équilibrées (si elles sont déséquilibrées, l’objet accélère):
 |
 |
|
| Équilibré | Déséquilibré | |
|---|---|---|
| Pas d’accélération | Accélération |
Exemple: Les forces au sommet de cette tour de pont sont en équilibre (il n’accélère pas):

Les câbles tirent vers le bas également vers la gauche et la droite, et cela est équilibré par la poussée vers le haut de la tour. (La tour pousse-t-elle? Oui! Imaginez que vous vous tenez là au lieu de la tour.) p>
Nous pouvons modéliser les forces comme ceci:

Et quand nous mettez-les tête-bêche, nous voyons qu’ils se referment sur eux-mêmes, ce qui signifie que l’effet net est nul:

Les forces sont en équilibre.
Les forces en équilibre sont dites en équilibre: il n’y a pas non plus de changement de mouvement.
Diagrammes de corps libres
La première étape est pour dessiner un diagramme de corps libre (également appelé diagramme de force)
Diagramme de corps libre: Une esquisse où un corps est coupé du monde à l’exception des forces agissant sur lui.
Dans l’exemple du pont, le diagramme du corps libre pour le sommet de la tour est:

Diagramme du corps libre
Cela aide nous devons penser clairement aux forces agissant sur le corps.
Exemple: Voiture sur une autoroute
Quelles sont les forces sur une voiture qui roule sur l’autoroute?

Le moteur travaille dur, alors pourquoi la voiture ne continue-t-elle pas à accélérer?
Parce que la conduite la force est équilibrée par:
- La résistance de l’air (en termes simples: th L’air résiste à la poussée),
- Résistance au roulement, également appelée friction de roulement (les pneus résistent à la modification de leur forme)

Diagramme de carrosserie libre
W est le poids de la voiture,
R1 et R2 sont la résistance au roulement des pneus,
N1 et N2 sont les forces de réaction (équilibrant le poids de la voiture).
Remarque: les roues en acier (comme sur les trains) ont moins de résistance au roulement, mais sont bien trop glissantes sur la route!
Calculs
La force est un vecteur. Un vecteur a une magnitude (taille) et une direction:

Nous pouvons modéliser les forces en dessinant des flèches de taille et de direction correctes . Comme ceci:
Exemple: admirer la vue
Brady se tient sur le bord d’un balcon soutenu par une poutre horizontale et une entretoise:

Il pèse 80 kg.
Quelles sont les forces?
Prenons la place sur laquelle il se tient et réfléchissons aux forces là-bas:

Son poids
Sa masse de 80 kg crée une force vers le bas due à la gravité.
La force est la masse multipliée par l’accélération: F = ma
L’accélération due à la gravité sur Terre est de 9,81 m / s2 , donc a = 9,81 m / s2
F = 80 kg × 9,81 m / s2
F = 785 N
Les autres forces
Les forces sont équilibrées, donc elles devraient se refermer sur elles-mêmes comme ceci:

Nous pouvons utiliser la trigonométrie pour le résoudre .
Parce que c’est un triangle rectangle, SOHCAHTOA aidera.
Pour la poutre, nous connaissons l’Adjacent, nous voulons connaître l’opposé, et « TOA » nous dit d’utiliser Tangent:
bronzé (60 ° ) = Poutre / 785 N
Poutre / 785 N = tan (60 °)
Faisceau = tan (60 °) × 785 N
Faisceau = 1,732 … × 785 N = 1360 N
Pour le Strut, nous connaissons l’Adjacent, nous voulons connaître l’Hypoténuse, et « CAH » nous dit d’utiliser Cosine:
cos (60 °) = 785 N / Jambe
Jambe × cos (60 °) = 785 N
Jambe = 785 N / cos (60 °)
Strut = 785 N / 0.5 = 1570 N
Résolu:

Il est intéressant de savoir combien de force est appliquée la poutre et la jambe de force par rapport au poids supporté!
Couple (ou moment)
Que faire si la poutre est juste coincée dans le mur (appelé cantilever)?

Il n’y a pas de jambe de force, alors qu’arrive-t-il aux forces?
Le diagramme du corps libre ressemble à ceci:

La force vers le haut R équilibre le poids vers le bas.
Avec seulement ces deux force le faisceau tournera comme une hélice! Mais il y a aussi un «effet de rotation» M appelé Moment (ou Torque) qui équilibre le tout:
Moment: Force fois la distance à angle droit.
Nous savons que le poids est 785 N, et nous devons également connaître la distance à angle droit, qui dans ce cas est de 3,2 m.
M = 785 N x 3,2 m = 2512 Nm
Et ce moment est ce qui empêche le faisceau de tourner.

Vous pouvez ressentir un moment en vous tenant à une canne à pêche.
En plus de maintenir son poids, vous devez l’empêcher de tourner vers le bas.
Friction
Boîte sur une rampe
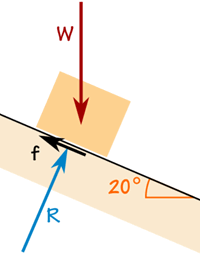
La boîte pèse 100 kg.
La force de frottement est suffisante pour la maintenir là où elle est.
La force de réaction R est perpendiculaire au rampe.
La boîte n’accélère pas, donc les forces sont en équilibre:
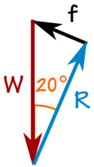
Les 100 kg de masse crée une force vers le bas due à la gravité:
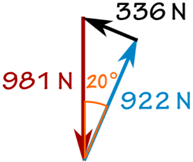
W = 100 kg × 9,81 m / s2 = 981 N
Nous pouvons utiliser SOHCAHTOA pour résoudre le triangle.
Friction f:
sin (20 °) = f / 981 N
f = sin (20 °) × 981 N = 336 N
Réaction N:
cos (20 °) = R / 981 N
R = cos (20 °) × 981 N = 922 N
Et nous obtenons:
Conseils pour dessiner des diagrammes de corps libres
- Dessinez le plus simplement possible. Une boîte suffit souvent.
- Les forces pointent dans la direction où elles agissent sur le corps
- flèches droites pour les forces
- flèches courbes pour les moments
Sam et Alex tirent une boîte
Les calculs peuvent parfois être plus faciles lorsque nous transformons la grandeur et la direction en x et y:
 |
< = > |  |
| Vecteur a dans les coordonnées polaires |
Vecteur a en coordonnées cartésiennes |
Vous pouvez lire comment les convertir en polaire et cartésien Coordonnées, mais voici un bref résumé:
Utilisons-les!