Tests paramétriques et non paramétriques pour comparer deux groupes ou plus

Statistiques: tests paramétriques et non paramétriques

Cette section couvre:

• Choix d’un test
• Tests paramétriques
• Tests non paramétriques

Choix d’un test

En termes de sélection d’un test statistique, la question la plus importante est « quelle est l’hypothèse principale de l’étude? » Dans certains cas, il n’y a pas d’hypothèse; l’enquêteur veut juste «voir ce qu’il y a». Par exemple, dans une étude de prévalence, il n’y a pas d’hypothèse à tester et la taille de l’étude est déterminée par la précision avec laquelle l’investigateur veut déterminer la prévalence. S’il n’y a pas d’hypothèse, alors il n’y a pas de test statistique. Il est important de décider a priori quelles hypothèses sont confirmatives (c’est-à-dire testent une relation présupposée) et lesquelles sont exploratoires (sont suggérées par les données). Aucune étude ne peut étayer toute une série d’hypothèses. Un plan raisonnable est de limiter sévèrement le nombre d’hypothèses de confirmation. Bien qu’il soit valide d’utiliser des tests statistiques sur les hypothèses suggérées par les données, les valeurs de P ne doivent être utilisées qu’à titre indicatif et les résultats sont considérés comme provisoires jusqu’à ce qu’ils soient confirmés par des études ultérieures. Un guide utile consiste à utiliser une correction de Bonferroni, qui indique simplement que si l’on teste n hypothèses indépendantes, on doit utiliser un niveau de signification de 0,05 / n. Ainsi, s’il y avait deux hypothèses indépendantes, un résultat ne serait déclaré significatif que si P < 0,025. Notez que, comme les tests sont rarement indépendants, il s’agit d’une procédure très conservatrice – c’est-à-dire une procédure qui est peu susceptible de rejeter l’hypothèse nulle. L’enquêteur devrait alors demander « les données sont-elles indépendantes? » Cela peut être difficile à décider, mais en règle générale, les résultats sur le même individu ou sur des individus appariés ne sont pas indépendants. Ainsi, les résultats d’un essai croisé, ou d’une étude cas-témoins dans laquelle les témoins ont été appariés aux cas par âge, sexe et classe sociale, ne sont pas indépendants.

• L’analyse doit refléter la conception , et donc une conception adaptée doit être suivie d’une analyse correspondante.
• Les résultats mesurés au fil du temps nécessitent une attention particulière. L’une des erreurs les plus courantes dans l’analyse statistique est de traiter les variables corrélées comme si elles étaient indépendantes. Par exemple, supposons que nous examinions le traitement des ulcères de jambe, dans lesquels certaines personnes avaient un ulcère sur chaque jambe. Nous pourrions avoir 20 sujets avec
  30 ulcères mais le nombre d’informations indépendantes est de 20 car l’état des ulcères sur chaque jambe pour une personne peut être influencé par l’état de santé de la personne et une analyse qui considérés comme des ulcères comme des observations indépendantes seraient incorrectes. Pour une analyse correcte des données mixtes appariées et non appariées, consultez un statisticien.

La question suivante est « quels types de données sont mesurées? » Le test utilisé doit être déterminé par les données. Le choix du test pour les données appariées ou appariées est décrit dans le tableau 1 et pour les données indépendantes dans le tableau 2.

Tableau 1 Choix du test statistique à partir d’une observation appariée ou appariée

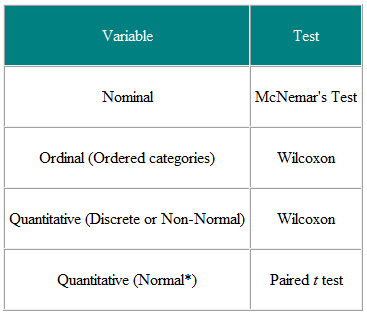
Il est utile de décider des variables d’entrée et des variables de résultat. Par exemple, dans un essai clinique, la variable d’entrée est le type de traitement – une variable nominale – et le résultat peut être une mesure clinique peut-être distribuée normalement. Le test requis est alors le test t (tableau 2). Cependant, si la variable d’entrée est continue, disons un score clinique, et que le résultat est nominal, disons guéri ou non guéri, la régression logistique est l’analyse requise. Un test t dans ce cas peut aider mais ne nous donnerait pas ce dont nous avons besoin, à savoir la probabilité de guérison pour une valeur donnée du score clinique. Comme autre exemple, supposons que nous ayons une étude transversale dans laquelle nous demandons à un échantillon aléatoire de personnes si elles pensent que leur médecin généraliste fait du bon travail, sur une échelle de cinq points, et nous souhaitons déterminer si les femmes ont une opinion plus élevée. des médecins généralistes que les hommes. La variable d’entrée est le sexe, qui est nominal. La variable de résultat est l’échelle ordinale à cinq points. L’opinion de chaque personne est indépendante des autres, nous avons donc des données indépendantes. À partir du tableau 2, nous devrions utiliser un test trend2 pour la tendance, ou un test Mann-Whitney U avec une correction pour les égalités (NB une égalité se produit là où deux ou plus les valeurs sont les mêmes, il n’y a donc pas d’ordre strictement croissant des rangs – là où cela se produit, on peut faire la moyenne des classements pour des valeurs liées). Notez cependant que si certaines personnes partagent un médecin généraliste et d’autres pas, les données ne le sont pas Une analyse indépendante et plus sophistiquée est nécessaire.Notez que ces tableaux ne doivent être considérés que comme des guides et que chaque cas doit être examiné selon ses mérites.

Tableau 2 Choix du test statistique pour les observations indépendantes

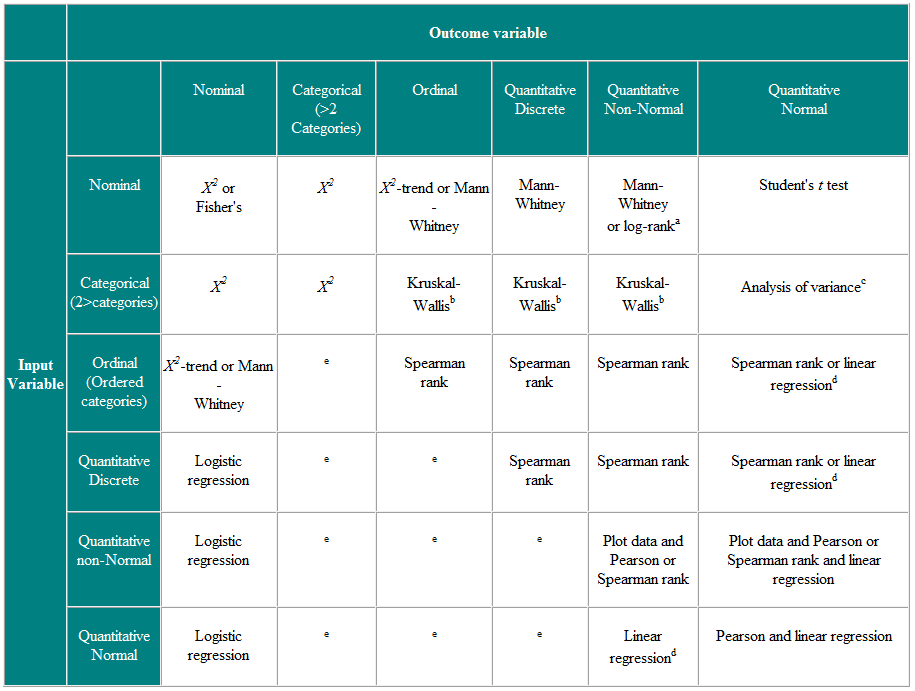
a Si les données sont censurées. b Le test de Kruskal-Wallis est utilisé pour comparer des variables ordinales ou non normales pour plus de deux groupes et est une généralisation du test U de Mann-Whitney. c L’analyse de la variance est une technique générale, et une version (analyse de variance unidirectionnelle) est utilisée pour comparer des variables normalement distribuées pour plus de deux groupes, et est l’équivalent paramétrique du Kruskal-Wallistest. d Si la variable de résultat est la variable dépendante, à condition que les résidus (les différences entre les valeurs observées et les réponses prédites de la régression) soient vraisemblablement distribués normalement, alors la distribution de la variable indépendante n’est pas importante. e Il existe un certain nombre de techniques plus avancées, comme la régression de Poisson, pour traiter ces situations. Cependant, ils nécessitent certaines hypothèses et il est souvent plus facile de dichotomiser la variable de résultat ou de la traiter comme continue.

Les tests paramétriques sont ceux qui font des hypothèses sur les paramètres de la distribution de la population à partir de laquelle l’échantillon est tiré . C’est souvent l’hypothèse que les données démographiques sont normalement distribuées. Les tests non paramétriques sont « sans distribution » et, en tant que tels, peuvent être utilisés pour des variables non normales. Le tableau 3 montre l’équivalent non paramétrique d’un certain nombre de tests paramétriques.

Tableau 3 Paramétrique et Tests non paramétriques pour comparer deux groupes ou plus

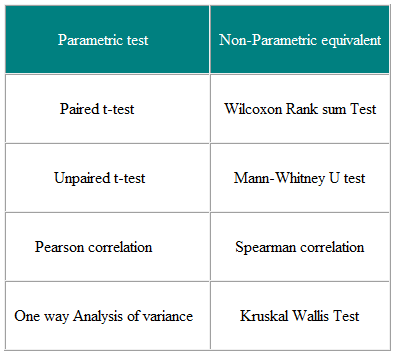
Les tests non paramétriques sont valables pour les données non distribuées normalement et Des données normalement distribuées, alors pourquoi ne pas les utiliser tout le temps?

Il semblerait prudent d’utiliser des tests non paramétriques dans tous les cas, ce qui éviterait la peine de tester la normalité. Les tests paramétriques sont préférés, cependant, pour les raisons suivantes:

1. Nous sommes rarement intéressés par un test de signification seul; nous aimerions dire quelque chose sur la population d’où proviennent les échantillons, et cela est mieux fait avec
estimations des paramètres et des intervalles de confiance.

2. Il est difficile de faire une modélisation flexible avec des tests non paramétriques, par exemple en permettant des facteurs de confusion utilisant plusieurs régression.

3. Les tests paramétriques ont généralement plus de puissance statistique que leurs équivalents non paramétriques. En d’autres termes, on est plus susceptible de détecter des différences significatives lorsqu’elles existent vraiment.

Les tests non paramétriques comparent-ils les médianes?

Il est communément admis qu’une Le test U de Mann-Whitney est en fait un test de différences de médianes. Cependant, deux groupes pourraient avoir la même médiane et pourtant avoir un test U de Mann-Whitney significatif. Considérez les données suivantes pour deux groupes, chacun avec 100 observations. Groupe 1: 98 (0), 1, 2; Groupe 2: 51 (0), 1, 48 (2). La médiane dans les deux cas est de 0, mais d’après le test de Mann-Whitney P < 0,0001. Ce n’est que si nous sommes prêts à faire l’hypothèse supplémentaire que la différence entre les deux groupes est simplement un changement d’emplacement (c’est-à-dire que la distribution des données dans un groupe est simplement décalée d’un montant fixe par rapport à l’autre) que nous pouvons dire que le test est un test de la différence des médianes. Cependant, si les groupes ont la même distribution, alors un changement d’emplacement déplacera les médianes et les moyennes du même montant et donc la différence des médianes est la même que la différence des moyennes. Ainsi, le test U de Mann-Whitney est également un test de la différence des moyennes. Quel est le lien entre le test U de Mann-Whitney et le test t? Si l’on devait entrer les rangs des données plutôt que les données elles-mêmes dans un programme de test t à deux échantillons, la valeur P obtenue serait très proche de celle produite par un test U de Mann-Whitney.