• K-Nearest Neighbor est l’un des algorithmes d’apprentissage automatique les plus simples basés sur sur la technique d’apprentissage supervisé.
• L’algorithme K-NN suppose la similitude entre le nouveau cas / données et les cas disponibles et place le nouveau cas dans la catégorie la plus similaire aux catégories disponibles.

K-NN stocke toutes les données disponibles et classe un nouveau point de données en fonction de la similitude. Cela signifie que lorsque de nouvelles données apparaissent, elles peuvent être facilement classées dans une catégorie de suite de puits en utilisant l’algorithme K-NN.

• L’algorithme K-NN peut être utilisé pour la régression ainsi que pour la classification, mais il est principalement utilisé pour les problèmes de classification.
• K-NN est un algorithme non paramétrique, ce qui signifie il ne fait aucune hypothèse sur les données sous-jacentes.
• Il est également appelé algorithme d’apprentissage paresseux car il n’apprend pas immédiatement de l’ensemble d’apprentissage au lieu de cela, il stocke l’ensemble de données et au moment de la classification, il effectue un action sur l’ensemble de données.
• L’algorithme KNN à la phase d’apprentissage stocke simplement l’ensemble de données et lorsqu’il obtient de nouvelles données, il classe ces données dans une catégorie qui est très similaire aux nouvelles données.
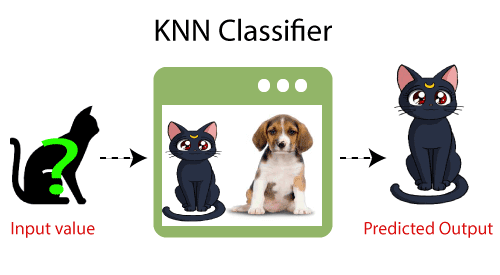
• Exemple: Supposons que nous ayons une image d’une créature qui ressemble à un chat et un chien, mais nous voulons savoir que c’est un chat ou un chien. Donc pour cette identification, nous pouvons utiliser l’algorithme KNN, car il fonctionne sur une mesure de similarité. Notre modèle KNN trouvera les caractéristiques similaires du nouvel ensemble de données aux images de chats et de chiens et, en fonction des caractéristiques les plus similaires, il le placera dans la catégorie des chats ou des chiens.

Pourquoi avons-nous besoin d’un algorithme K-NN?

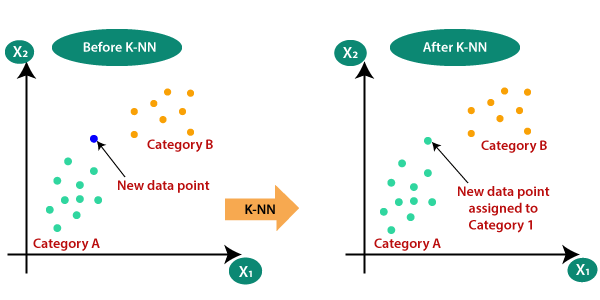
Supposons qu’il y ait deux catégories, à savoir, la catégorie A et la catégorie B, et que nous ayons un nouveau point de données x1, donc ce point de données se trouvera dans laquelle de ces catégories. Pour résoudre ce type de problème, nous avons besoin d’un algorithme K-NN. Avec l’aide de K-NN, nous pouvons facilement identifier la catégorie ou la classe d’un ensemble de données particulier. Considérez le diagramme ci-dessous:

Comment fonctionne K-NN?

Le fonctionnement de K-NN peut être expliqué sur la base de l’algorithme ci-dessous:

• Étape 1: Sélectionnez le nombre K des voisins
• Étape 2: Calculez la distance euclidienne du nombre K de voisins
• Étape-3: Prenez les K voisins les plus proches selon la distance euclidienne calculée.
• Étape-4: Parmi ces k voisins, comptez le nombre de points de données dans chaque catégorie.
• Étape-5: Attribuez les nouveaux points de données à cette catégorie pour laquelle le nombre de voisins est maximum.
• Étape-6: Notre modèle est prêt.

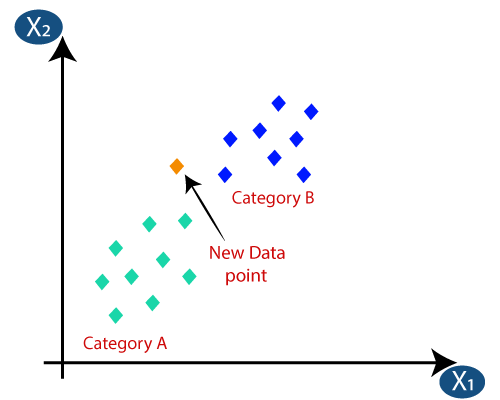
Supposons que nous ayons un nouveau point de données et que nous devions le mettre dans la catégorie requise. Considérez l’image ci-dessous:

• Tout d’abord, nous choisirons le nombre de voisins, nous choisirons donc le k = 5.
• Ensuite, nous calculerons la distance euclidienne entre les points de données. La distance euclidienne est la distance entre deux points, que nous avons déjà étudiée en géométrie. Il peut être calculé comme suit:

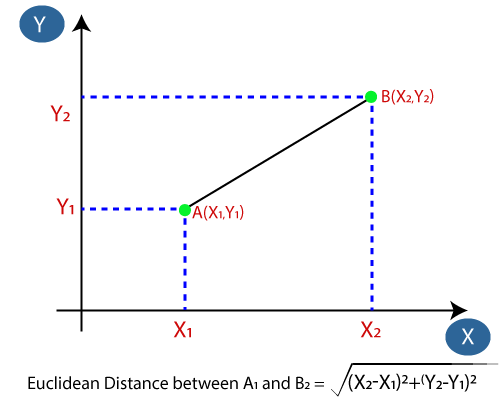
• En calculant la distance euclidienne, nous avons obtenu les voisins les plus proches, comme trois voisins les plus proches dans la catégorie A et deux voisins les plus proches dans la catégorie B. Considérez l’image ci-dessous:

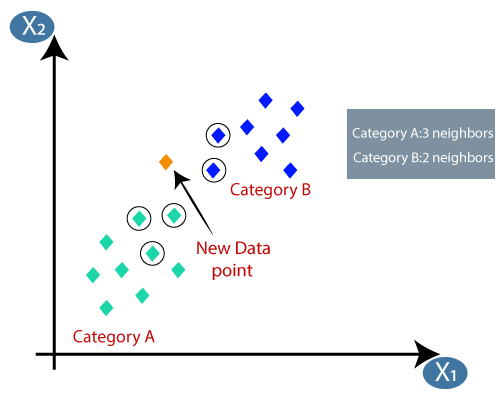
• Comme nous pouvons le voir, les 3 voisins les plus proches sont de la catégorie A, donc ce nouveau point de données doit appartenir à la catégorie A.

Comment sélectionner la valeur de K dans l’algorithme K-NN?

Voici quelques points à rappelez-vous en sélectionnant la valeur de K dans l’algorithme K-NN:

• Il n’y a pas de moyen particulier de déterminer la meilleure valeur pour « K », nous devons donc essayer certaines valeurs pour trouver la meilleure hors d’eux. La valeur la plus préférée pour K est 5.
• Une valeur très faible pour K telle que K = 1 ou K = 2, peut être bruyante et entraîner des effets de valeurs aberrantes dans le modèle.
• Les grandes valeurs pour K sont bonnes, mais cela peut rencontrer des difficultés.

Avantages de l’algorithme KNN:

• Il est simple à implémenter.
• / li>
• Il est robuste aux données d’entraînement bruyantes
• Il peut être plus efficace si les données d’entraînement sont volumineuses.

Inconvénients de l’algorithme KNN:

• Il faut toujours déterminer la valeur de K qui peut être complexe un certain temps.
• Le coût de calcul est élevé en raison du calcul de la distance entre les points de données pour tous les échantillons d’apprentissage .

Implémentation Python de l’algorithme KNN

Pour faire l’implémentation Python de l’algorithme K-NN, nous utiliserons le même problème et ensemble de données que nous avons utilisé dans Régression logistique. Mais ici, nous allons améliorer les performances du modèle. Voici la description du problème:

Problème pour l’algorithme K-NN: Il existe un constructeur automobile qui a fabriqué une nouvelle voiture SUV.La société souhaite diffuser les annonces aux utilisateurs intéressés par l’achat de ce SUV. Donc, pour ce problème, nous avons un ensemble de données qui contient des informations sur plusieurs utilisateurs via le réseau social. L’ensemble de données contient beaucoup d’informations, mais le salaire et l’âge estimés que nous prendrons en considération pour la variable indépendante et la variable achetée est pour la variable dépendante. Voici le jeu de données:

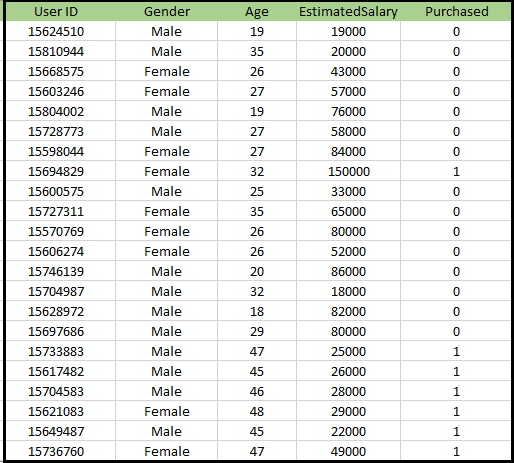
Étapes de mise en œuvre de l’algorithme K-NN:

• Étape de prétraitement des données
• Ajustement de l’algorithme K-NN à l’ensemble d’apprentissage
• Prédiction du résultat du test
• Exactitude du test du résultat (création de la matrice de confusion)
• Visualisation du résultat de l’ensemble de test.

Étape de pré-traitement des données:

L’étape de prétraitement des données restera exactement la même que la régression logistique. Ci-dessous le code pour cela:

En exécutant le code ci-dessus, notre ensemble de données est importé dans notre programme et bien prétraité. Après la mise à l’échelle des caractéristiques, notre ensemble de données de test ressemblera à:

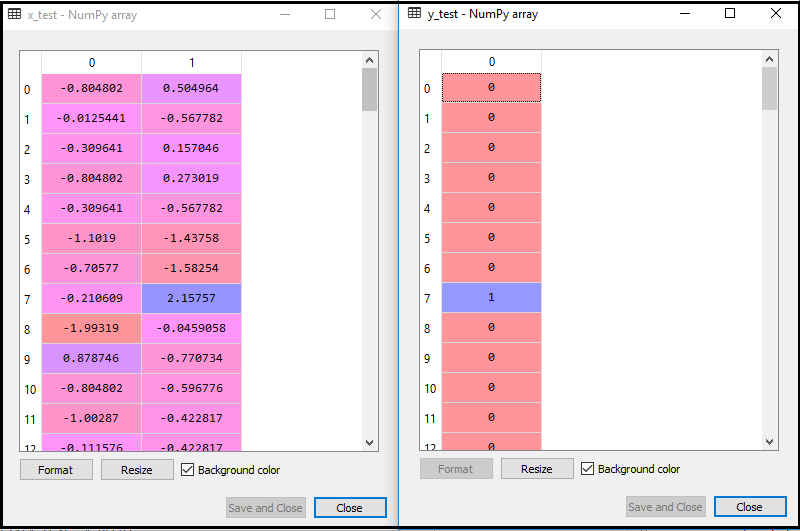
À partir de la sortie ci-dessus im âge, nous pouvons voir que nos données sont mises à l’échelle avec succès.

• Ajustement du classificateur K-NN aux données d’entraînement:
  Nous allons maintenant adapter le classificateur K-NN aux données d’entraînement. Pour ce faire, nous allons importer la classe KNeighborsClassifier de la bibliothèque Sklearn Neighbours. Après avoir importé la classe, nous allons créer l’objet Classifier de la classe. Le paramètre de cette classe sera
  • n_neighbors: Pour définir les voisins requis de l’algorithme. Habituellement, cela prend 5.
  • metric = « minkowski »: C’est le paramètre par défaut et il décide de la distance entre les points.
  • p = 2: C’est équivalent à la norme Métrique euclidienne.

  Ensuite, nous ajusterons le classificateur aux données d’entraînement. Voici le code pour cela:

Sortie: En exécutant le code ci-dessus, nous obtiendrons la sortie comme:

• Prédire le résultat du test: Pour prédire le résultat du test, nous allons créer un vecteur y_pred comme nous l’avons fait dans la régression logistique. Voici le code pour cela:

Sortie:

La sortie pour le code ci-dessus sera:

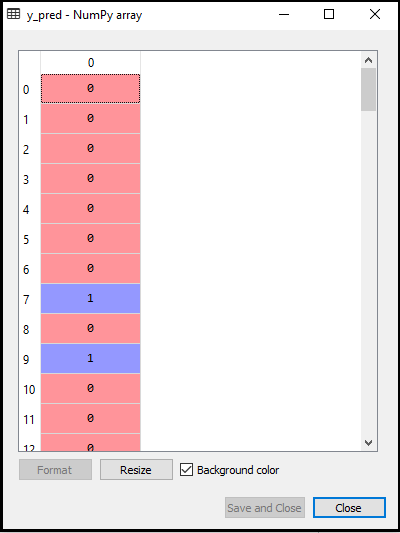
• Création de la matrice de confusion:
  Nous allons maintenant créer la matrice de confusion pour notre modèle K-NN pour voir la précision du classificateur. Voici le code pour cela:

Dans le code ci-dessus, nous avons importé la fonction confusion_matrix et l’avons appelée en utilisant la variable cm.

Sortie: En exécutant le code ci-dessus, nous obtiendrons la matrice comme ci-dessous:

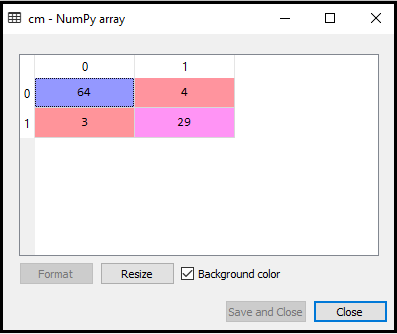
Dans l’image ci-dessus, nous pouvons voir il y a 64 + 29 = 93 prédictions correctes et 3 + 4 = 7 prédictions incorrectes, alors que, dans la régression logistique, il y avait 11 prédictions incorrectes. Nous pouvons donc dire que les performances du modèle sont améliorées en utilisant l’algorithme K-NN.

• Visualisation du résultat de l’ensemble d’entraînement:
  Maintenant, nous allons visualiser le résultat de l’ensemble d’entraînement pour K -Modèle NN. Le code restera le même que nous l’avons fait dans la régression logistique, à l’exception du nom du graphique. Voici le code pour cela:

Sortie:

En exécutant le code ci-dessus, nous obtiendrons le graphique ci-dessous:

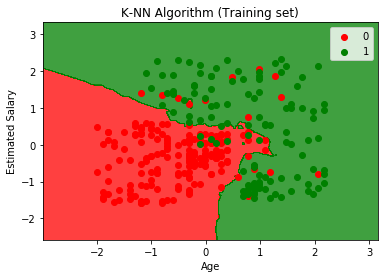
Le graphique de sortie est différent du graphique que nous avons produit dans la régression logistique. Cela peut être compris dans les points ci-dessous:

• Comme nous pouvons le voir, le graphique montre le point rouge et les points verts. Les points verts sont pour la variable Acheté (1) et Points rouges pour la variable Non acheté (0).
• Le graphique montre une limite irrégulière au lieu de montrer une ligne droite ou une courbe car il s’agit d’un algorithme K-NN, c’est-à-dire trouver le voisin le plus proche.
• Le graphique a classé les utilisateurs dans les bonnes catégories, car la plupart des utilisateurs qui n’ont pas acheté le SUV sont dans la région rouge et les utilisateurs qui ont acheté le SUV sont dans la région verte.
• Le graphique montre un bon résultat, mais il y a quand même des points verts dans la région rouge et des points rouges dans la région verte. Mais ce n’est pas un gros problème car ce modèle évite les problèmes de surajustement.
• Notre modèle est donc bien entraîné.
• Visualisation du résultat de l’ensemble de test:
  Après l’entraînement du modèle, nous allons maintenant tester le résultat en mettant un nouvel ensemble de données, c’est-à-dire Jeu de données de test. Le code reste le même, sauf quelques modifications mineures: telles que x_train et y_train seront remplacées par x_test et y_test.
  Voici le code correspondant:

Sortie:

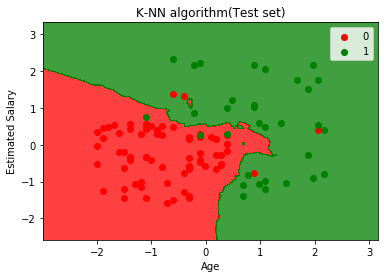
Le graphique ci-dessus montre la sortie de l’ensemble de données de test. Comme nous pouvons le voir dans le graphique, la sortie prévue est bonne bon car la plupart des points rouges sont dans la région rouge et la plupart des points verts sont dans la région verte.

Cependant, il y a quelques points verts dans la région rouge et quelques points rouges dans la région verte. Ce sont donc les observations incorrectes que nous avons observées dans la matrice de confusion (7 Sortie incorrecte).