La pente d’une colline est appelée pente. Il en va de même pour la pente d’une ligne. La pente est définie comme le rapport du changement vertical entre deux points, la montée, au changement horizontal entre les deux mêmes points, la course.

$$ pente = \ frac {montée} {course} = \ frac {change \: in \: y} {change \: in \: x} $$

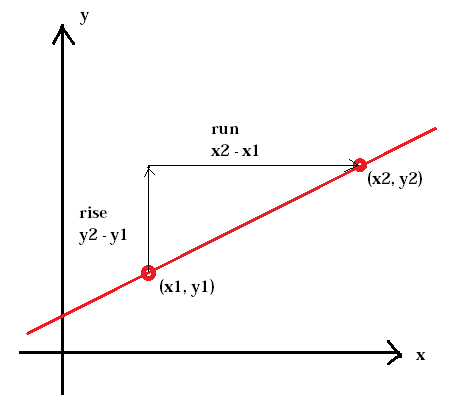
Le la pente d’une ligne est généralement représentée par la lettre m. (x1, y1) représente le premier point tandis que (x2, y2) représente le deuxième point.

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2 } \, -x_ {1}} $$

Il est important de garder les coordonnées x et y dans le même ordre au numérateur et au dénominateur sinon vous obtiendrez la mauvaise pente.

Exemple

Trouvez la pente de la ligne

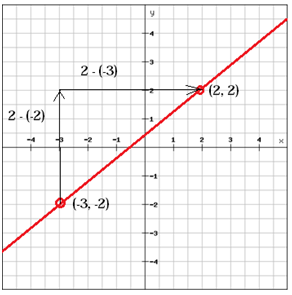
(x1, y1 ) = (-3, -2) et (x2, y2) = (2, 2)

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ { 2} \, -x_ {1}} = \ frac {2- \ left (-2 \ right)} {2- \ left (-3 \ right)} = \ frac {2 + 2} {2 + 3} = \ frac {4} {5} $$

Une ligne avec une pente positive (m > 0), comme la ligne ci-dessus, monte de gauche à à droite alors qu’une ligne à pente négative (m < 0) tombe de gauche à droite.

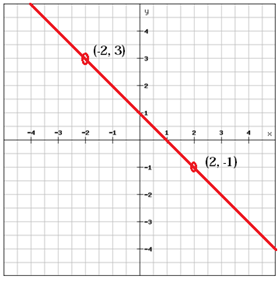
$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2} \, -x_ {1}} = \ frac {\ gauche (-1 \ droite) -3} {2- \ left (-2 \ right)} = \ frac {-1-3} {2 + 2} = \ frac {-4} {4} = – 1 $$

Si deux droites ont la même pente, les droites sont dites p arallel.

Vous pouvez exprimer une fonction linéaire en utilisant la forme d’interception de pente.

$$ y = mx + b $$

$$ m = pente $ $

$$ b = y – intercept $$

Leçon vidéo

Trouvez la pente