MATH 1314: Algèbre universitaire
Alors que les asymptotes verticales décrivent le comportement d’un graphe lorsque la sortie devient très grande ou très petite, les asymptotes horizontales aident à décrire le comportement d’un graphe comme le l’entrée devient très grande ou très petite. Rappelez-vous que le comportement final d’un polynôme reflétera celui du terme principal. De même, le comportement final d’une fonction rationnelle reflétera celui du rapport des termes principaux des fonctions numérateur et dénominateur.
Il y a trois résultats distincts lors de la vérification des asymptotes horizontales:
Cas 1: Si le degré du dénominateur > degré du numérateur, il y a une asymptote horizontale à y = 0.

Cas 2: Si le degré du dénominateur < degré du numérateur par un, on obtient une asymptote oblique.

Notez que, même si le graphique d’une fonction rationnelle ne traversera jamais une asymptote verticale, le graphique peut ou non traverser une horizontale ou une inclinaison comme ymptote. Aussi, bien que le graphique d’une fonction rationnelle puisse avoir de nombreuses asymptotes verticales, le graphique aura au plus une asymptote horizontale (ou oblique).
Il convient de noter que, si le degré du numérateur est plus grand que le degré du dénominateur par plus d’un, le comportement final du graphe imite le comportement de la fraction de comportement final réduite. Par exemple, si nous avions la fonction
avec comportement final
le comportement final du graphe ressemblerait à celui d’un polynôme pair avec un coefficient de tête positif.
Note générale: Asymptotes horizontales des fonctions rationnelles
L’asymptote horizontale d’une fonction rationnelle peut être déterminé en regardant les degrés du numérateur et du dénominateur.
- Le degré du numérateur est inférieur au degré du dénominateur: asymptote horizontale en y = 0.
- Le degré du numérateur est supérieur au degré de dénominateur de un: pas d’asymptote horizontale; asymptote oblique.
- Le degré du numérateur est égal au degré du dénominateur: asymptote horizontale au rapport des coefficients principaux.
Exemple 9: Identifier les asymptotes horizontales et verticales
Trouver les asymptotes horizontales et verticales de la fonction
Solution
Tout d’abord, notez que cette fonction n’a pas de facteurs communs, donc il n’y a pas de discontinuités amovibles potentielles.
La fonction aura des asymptotes verticales lorsque le dénominateur est zéro, ce qui rendra la fonction indéfinie. Le dénominateur sera zéro à x = 1, -2, text {et} 5 \, indiquant des asymptotes verticales à ces valeurs.
Le numérateur a le degré 2, tandis que le dénominateur a le degré 3. Depuis le degré du dénominateur est supérieur au degré du numérateur, le dénominateur croîtra plus vite que le numérateur, ce qui amènera les sorties à tendre vers zéro à mesure que les entrées deviennent grandes, et donc, lorsque xto pm infty, vola (xright) à 0 \. Cette fonction aura une asymptote horizontale à y = 0 \.
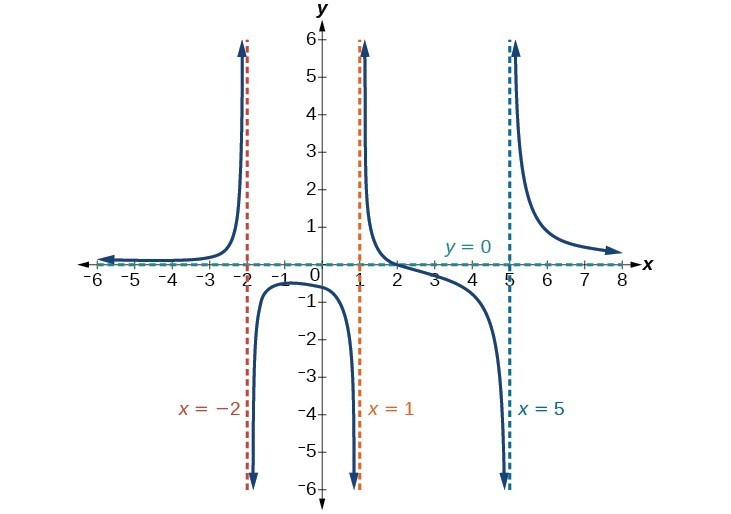
Figure 15
Note générale: Intercepts de fonctions rationnelles
Une fonction rationnelle aura un ordonnée à l’origine lorsque l’entrée est zéro, si la fonction est définie à zéro. Une fonction rationnelle n’aura pas d’ordonnée à l’origine si la fonction n’est pas définie à zéro.
De même, une fonction rationnelle aura des abscisses aux entrées qui font que la sortie est nulle. Étant donné qu’une fraction n’est égale à zéro que lorsque le numérateur est zéro, les abscisses à l’origine ne peuvent se produire que lorsque le numérateur de la fonction rationnelle est égal à zéro.
Try It 7
Étant donné la fonction réciproque au carré qui est décalée vers la droite de 3 unités et vers le bas de 4 unités, écrivez ceci comme une fonction rationnelle. Ensuite, trouvez les intersections x et y et les asymptotes horizontales et verticales.
Solution