Parametrische und nicht parametrische Tests zum Vergleichen von zwei oder mehr Gruppen

Statistik: Parametrische und nicht parametrische Tests

Dieser Abschnitt behandelt:

• Auswählen eines Tests
• Parametrische Tests
• Nicht parametrische Tests

Auswählen eines Tests

Bei der Auswahl eines statistischen Tests lautet die wichtigste Frage: „Was ist die Hauptstudienhypothese?“ In einigen Fällen gibt es keine Hypothese; Der Ermittler will nur „sehen, was da ist“. Beispielsweise gibt es in einer Prävalenzstudie keine zu testende Hypothese, und die Größe der Studie wird dadurch bestimmt, wie genau der Prüfer die Prävalenz bestimmen möchte. Wenn es keine Hypothese gibt, gibt es keinen statistischen Test. Es ist wichtig, a priori zu entscheiden, welche Hypothesen bestätigend sind (dh eine vorausgesetzte Beziehung testen) und welche explorativ sind (was aus den Daten hervorgeht). Keine einzelne Studie kann eine ganze Reihe von Hypothesen stützen. Ein vernünftiger Plan ist es, die Anzahl der bestätigenden Hypothesen stark zu begrenzen. Obwohl es gültig ist, statistische Tests für Hypothesen zu verwenden, die von den Daten vorgeschlagen werden, sollten die P-Werte nur als Richtlinien verwendet und die Ergebnisse als vorläufig behandelt werden, bis sie durch nachfolgende Studien bestätigt werden. Ein nützlicher Leitfaden ist die Verwendung einer Bonferroni-Korrektur, die einfach besagt, dass beim Testen von n unabhängigen Hypothesen ein Signifikanzniveau von 0,05 / n verwendet werden sollte. Wenn es also zwei unabhängige Hypothesen gäbe, würde ein Ergebnis nur dann als signifikant deklariert, wenn P < 0,025. Da Tests selten unabhängig sind, ist dies ein sehr konservatives Verfahren – d. H. Eines, bei dem es unwahrscheinlich ist, dass die Nullhypothese verworfen wird. Der Ermittler sollte dann fragen: „Sind die Daten unabhängig?“ Dies kann schwierig zu entscheiden sein, aber als Faustregel sind Ergebnisse für dieselbe Person oder für übereinstimmende Personen nicht unabhängig. Daher sind die Ergebnisse einer Crossover-Studie oder einer Fall-Kontroll-Studie, in der die Kontrollen nach Alter, Geschlecht und sozialer Klasse auf die Fälle abgestimmt wurden, nicht unabhängig.

• Die Analyse sollte das Design widerspiegeln Auf ein abgestimmtes Design sollte daher eine übereinstimmende Analyse folgen.
• Die über die Zeit gemessenen Ergebnisse erfordern besondere Sorgfalt. Einer der häufigsten Fehler bei der statistischen Analyse besteht darin, korrelierte Variablen so zu behandeln, als wären sie unabhängig. Nehmen wir zum Beispiel an, wir haben uns mit der Behandlung von Beingeschwüren befasst, bei denen einige Menschen an jedem Bein ein Geschwür hatten. Wir haben vielleicht 20 Probanden mit 30 Geschwüren, aber die Anzahl der unabhängigen Informationen beträgt 20, da der Zustand der Geschwüre an jedem Bein für eine Person durch den Gesundheitszustand der Person und eine Analyse dieser Faktoren beeinflusst werden kann Geschwüre als unabhängige Beobachtungen zu betrachten, wäre falsch. Für eine korrekte Analyse von gemischten gepaarten und ungepaarten
  Daten wenden Sie sich an einen Statistiker.

Die nächste Frage lautet: „Welche Arten von Daten werden gemessen?“ Der verwendete Test sollte anhand der Daten bestimmt werden. Die Wahl des Tests für übereinstimmende oder gepaarte Daten ist in Tabelle 1 und für unabhängige Daten in Tabelle 2 beschrieben.

Tabelle 1 Auswahl des statistischen Tests aus gepaarten oder übereinstimmenden Beobachtungen

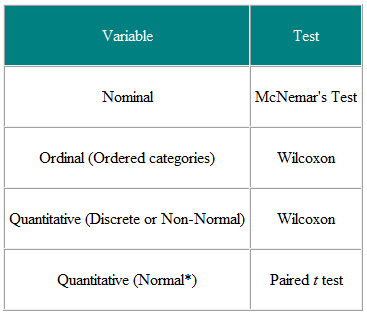
Es ist hilfreich, die Eingabevariablen und die Ergebnisvariablen zu bestimmen. In einer klinischen Studie ist die Eingabevariable beispielsweise die Art der Behandlung – eine nominelle Variable – und das Ergebnis kann eine klinische Maßnahme sein, die möglicherweise normal verteilt ist. Der erforderliche Test ist dann der t-Test (Tabelle 2). Wenn die Eingabevariable jedoch kontinuierlich ist, z. B. ein klinischer Score, und das Ergebnis nominal ist, z. B. geheilt oder nicht geheilt, ist die logistische Regression die erforderliche Analyse. Ein t-Test in diesem Fall kann helfen, würde uns aber nicht das geben, was wir benötigen, nämlich die Wahrscheinlichkeit einer Heilung für einen bestimmten Wert des klinischen Scores. Nehmen wir als weiteres Beispiel an, wir haben eine Querschnittsstudie, in der wir eine zufällige Stichprobe von Menschen auf einer Fünf-Punkte-Skala fragen, ob sie glauben, dass ihr Hausarzt gute Arbeit leistet, und wir möchten feststellen, ob Frauen eine höhere Meinung haben von Allgemeinärzten als Männer haben. Die Eingabevariable ist das nominelle Geschlecht. Die Ergebnisvariable ist die Fünf-Punkte-Ordnungsskala. Die Meinung jeder Person ist unabhängig von den anderen, daher haben wir unabhängige Daten. Aus Tabelle 2 sollten wir einen χ2-Test für den Trend oder einen Mann-Whitney-U-Test mit einer Korrektur für Bindungen verwenden (NB, eine Bindung tritt auf, wenn zwei oder mehr Die Werte sind die gleichen, daher gibt es keine streng ansteigende Reihenfolge der Ränge. In diesem Fall kann man die Ränge für gebundene Werte mitteln. Beachten Sie jedoch, dass einige Personen einen Allgemeinarzt teilen und andere nicht, die Daten jedoch nicht Es ist eine unabhängige und differenziertere Analyse erforderlich. Beachten Sie, dass diese Tabellen nur als Richtlinien dienen sollten und jeder Fall für sich betrachtet werden sollte.

Tabelle 2 Auswahl des statistischen Tests für unabhängige Beobachtungen

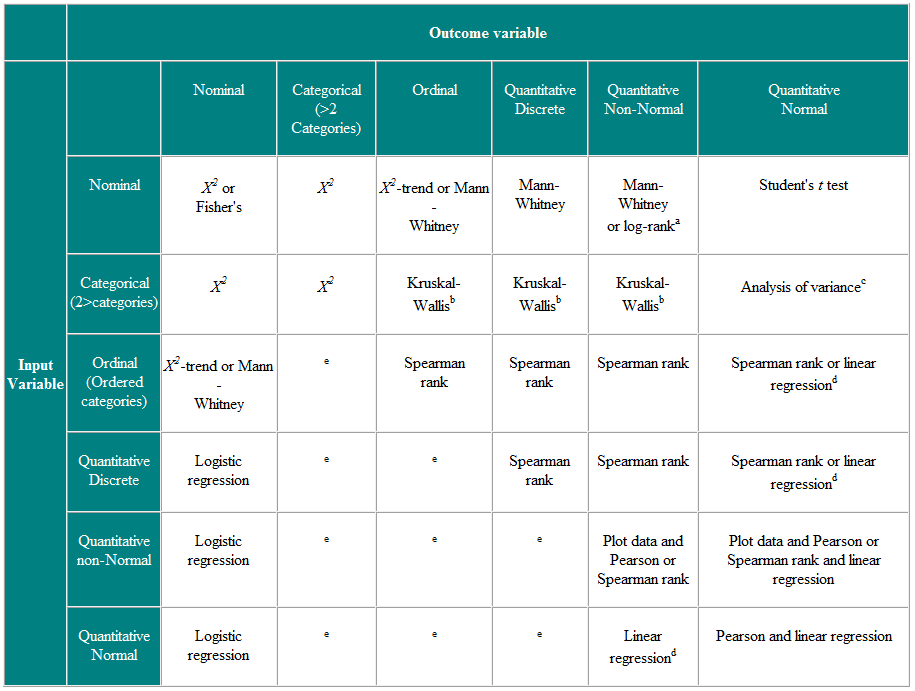
a Wenn Daten zensiert werden. b Der Kruskal-Wallis-Test wird zum Vergleichen von ordinalen oder nicht normalen Variablen für mehr als zwei Gruppen verwendet und ist eine Verallgemeinerung des Mann-Whitney-U-Tests. c Die Varianzanalyse ist eine allgemeine Technik, und eine Version (Einweg-Varianzanalyse) wird verwendet, um normalverteilte Variablen für mehr als zwei Gruppen zu vergleichen. Sie ist das parametrische Äquivalent des Kruskal-Wallistest. d Wenn die Ergebnisvariable die abhängige Variable ist, ist die Verteilung der unabhängigen Variablen nicht wichtig, sofern die Residuen (die Unterschiede zwischen den beobachteten Werten und den vorhergesagten Antworten aus der Regression) plausibel normalverteilt sind. e Es gibt eine Reihe fortgeschrittener Techniken wie die Poisson-Regression, um mit diesen Situationen umzugehen. Sie erfordern jedoch bestimmte Annahmen, und es ist oft einfacher, die Ergebnisvariable entweder zu dichotomisieren oder als kontinuierlich zu behandeln.

Parametrische Tests sind solche, die Annahmen über die Parameter der Populationsverteilung treffen, aus der die Stichprobe gezogen wird . Dies ist häufig die Annahme, dass die Bevölkerungsdaten normal verteilt sind. Nichtparametrische Tests sind „verteilungsfrei“ und können als solche für nicht normale Variablen verwendet werden. Tabelle 3 zeigt das nichtparametrische Äquivalent einer Reihe von parametrischen Tests.

Tabelle 3 Parametrisch und Nichtparametrische Tests zum Vergleichen von zwei oder mehr Gruppen

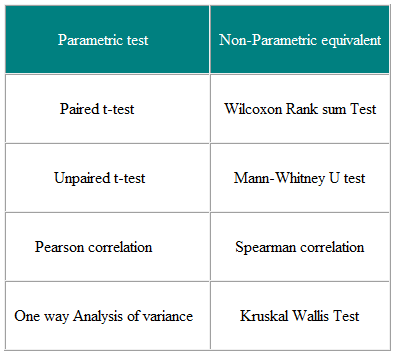
Nichtparametrische Tests gelten sowohl für nicht normalverteilte Daten als auch für Normalverteilte Daten, warum also nicht die ganze Zeit verwenden?

Es erscheint ratsam, in allen Fällen nichtparametrische Tests zu verwenden, was das Testen der Normalität erspart. Parametrische Tests werden bevorzugt. Aus folgenden Gründen:

1. Wir sind selten nur an einem Signifikanztest interessiert, wir möchten etwas über die Population sagen, aus der die Proben stammen, und dies geschieht am besten mit
Schätzungen von Parametern und Konfidenzintervallen.

2. Es ist schwierig, eine flexible Modellierung mit nichtparametrischen Tests durchzuführen, beispielsweise um Störfaktoren unter Verwendung mehrerer zu berücksichtigen Regression.

3. Parametrische Tests haben normalerweise eine höhere statistische Aussagekraft als ihre nichtparametrischen Äquivalente. Mit anderen Worten, es ist wahrscheinlicher, dass signifikante Unterschiede festgestellt werden, wenn sie tatsächlich existieren.

Vergleichen nichtparametrische Tests Mediane?

Es wird allgemein angenommen, dass a Der Mann-Whitney-U-Test ist in der Tat ein Test für Unterschiede im Median. Zwei Gruppen könnten jedoch den gleichen Median haben und dennoch einen signifikanten Mann-Whitney-U-Test haben. Betrachten Sie die folgenden Daten für zwei Gruppen mit jeweils 100 Beobachtungen. Gruppe 1: 98 (0), 1, 2; Gruppe 2: 51 (0), 1, 48 (2). Der Median ist in beiden Fällen 0, aber aus dem Mann-Whitney-Test P < 0,0001. Nur wenn wir bereit sind, die zusätzliche Annahme zu treffen, dass der Unterschied zwischen den beiden Gruppen einfach eine Ortsverschiebung ist (dh die Verteilung der Daten in einer Gruppe wird einfach um einen festen Betrag von der anderen verschoben), können wir das sagen Der Test ist ein Test des Medianunterschieds. Wenn die Gruppen jedoch die gleiche Verteilung haben, werden durch eine Verschiebung des Standorts die Mediane und Mittelwerte um den gleichen Betrag verschoben, sodass der Unterschied in den Medianen dem Unterschied in den Mittelwerten entspricht. Somit ist der Mann-Whitney-U-Test auch ein Test für den Mittelwertunterschied. In welcher Beziehung steht der Mann-Whitney-U-Test zum t-Test? Wenn man die Ränge der Daten anstelle der Daten selbst in ein t-Testprogramm mit zwei Stichproben eingeben würde, wäre der erhaltene P-Wert sehr nahe an dem, der durch einen Mann-Whitney-U-Test erzeugt wurde