A központi határ tétele azt mondja nekünk, hogy amint a mintaméretek nagyobbak lesznek, az átlag mintavételi eloszlása normálisan eloszlik, egyenletes ha az egyes mintákon belüli adatok általában nem oszlanak meg.

Ezt valós adatokban láthatjuk. Dolgozzunk az AlcoholYear változóval az NHANES eloszlásban, amely erősen ferde, amint az az ábra bal paneljén látható ?? Ez a disztribúció jobb szó híján funky – és határozottan nem szokott terjeszteni. Most nézzük meg ennek a változónak az átlagának mintavételi eloszlását. A 12.2. Ábra mutatja ennek a változónak a mintavételi eloszlását, amelyet úgy kapunk meg, hogy többször 50-es méretű mintákat veszünk az NHANES adatkészletből, és az átlagot vesszük. Az eredeti adatok egyértelmű nem normális jellege ellenére a mintavételi eloszlás figyelemre méltóan közel van a normálishoz.

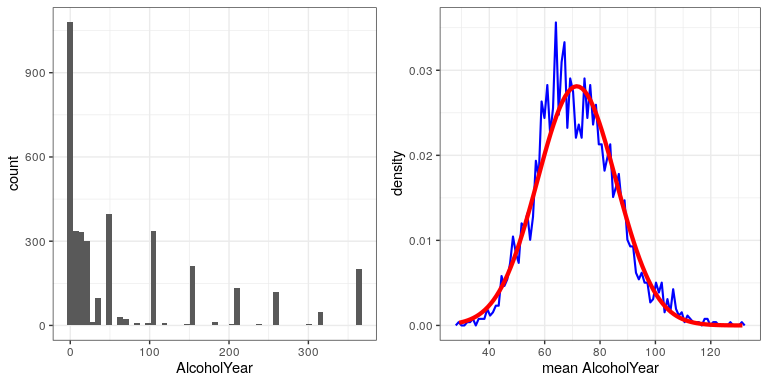bra: 12.2. ábra: Balra: Az AlcoholYear változó eloszlása az NHANES adatkészletben, amely tükrözi az egy éven át elfogyasztott napok számát. Jobbra: Az AlcoholYear átlagának mintavételi eloszlása az NHANES adatkészletben, amelyet 50-es méretű ismételt minták kék színű felvételével kaptunk. A normál eloszlás azonos átlaggal és szórással piros színnel jelenik meg.

A központi határ tétel fontos a statisztikák szempontjából, mert lehetővé teszi számunkra, hogy biztonságosan feltételezzük az átlag mintavételi eloszlása a legtöbb esetben normális lesz. Ez azt jelenti, hogy kihasználhatjuk azokat a statisztikai technikákat, amelyek normális eloszlást feltételeznek, amint azt a következő szakaszban láthatjuk