A domb meredekségét lejtőnek nevezzük. Ugyanez vonatkozik a vonal meredekségére is. A meredekség a két pont, az emelkedés és az ugyanazon két pont, a futás közötti vízszintes változás aránya.

$$ slope = \ frac {emelkedés} {futás} = \ frac {change \: in \: y} {change \: in \: x} $$

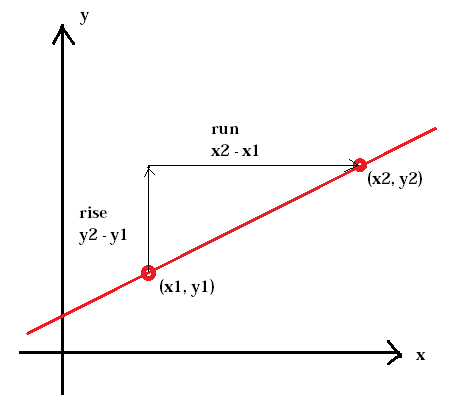
A egy vonal meredekségét általában m betű képviseli. (x1, y1) az első pontot, míg (x2, y2) a második pontot jelenti.

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2 } \, -x_ {1}} $$

Fontos, hogy az x-és y-koordinátákat ugyanabban a sorrendben tartsuk mind a számlálóban, mind a nevezőben, különben rossz lejtést kapunk.

Példa

Keresse meg a vonal meredekségét

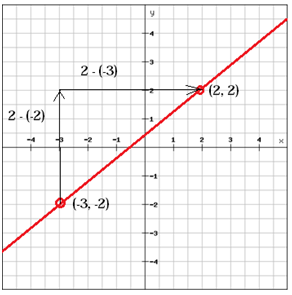
(x1, y1 ) = (-3, -2) és (x2, y2) = (2, 2)

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ { 2} \, -x_ {1}} = \ frac {2- \ bal (-2 \ jobb)} {2- \ bal (-3 \ jobb)} = \ frac {2 + 2} {2 + 3} = \ frac {4} {5} $$

Egy pozitív lejtésű (m > 0) vonal, amint a fenti vonal balról felfelé emelkedik jobbra, míg egy negatív lejtésű (m < 0) vonal balról jobbra esik.

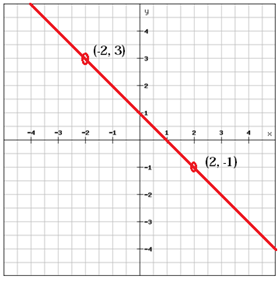
$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2} \, -x_ {1}} = \ frac {\ bal (-1 \ jobb) -3} {2- \ bal (-2 \ jobb)} = \ frac {-1-3} {2 + 2} = \ frac {-4} {4} = – 1 $$

Ha két egyenesnek ugyanaz a lejtése, akkor a vonalakat p-nek mondják párhuzamos.

Lineáris függvényt fejezhet ki a meredekség-elfogó űrlap segítségével.

$$ y = mx + b $$

$$ m = slope $ $

$$ b = y – elfogja a $$

videótanulót

Keresse meg a lejtőt