Parametrikus és nem parametrikus tesztek két vagy több csoport összehasonlítására

Statisztika: Parametrikus és nem parametrikus tesztek

Ez a szakasz kiterjed:

• Teszt kiválasztása
• Parametrikus tesztek
• Nem paraméteres tesztek

Teszt kiválasztása

A statisztikai teszt kiválasztása szempontjából a legfontosabb kérdés: “mi a fő tanulmányi hipotézis?” Bizonyos esetekben nincs hipotézis; a nyomozó csak “meg akarja nézni, mi van”. Például egy prevalencia vizsgálatban nincs hipotézis, amelyet tesztelni lehet, és a vizsgálat nagyságát az határozza meg, hogy a vizsgáló mennyire pontosan akarja meghatározni a prevalenciát. Ha nincs hipotézis, akkor nincs statisztikai teszt. Fontos eleve eldönteni, hogy mely hipotézisek igazolják (vagyis tesztelnek valamilyen feltételezett kapcsolatot), és melyek feltáró jellegűek (az adatok javasolják). Egyetlen tanulmány sem támasztja alá a hipotézisek egész sorozatát. Ésszerű terv a megerősítő hipotézisek számának szigorú korlátozása. Bár az adatok által javasolt hipotéziseken statisztikai teszteket lehet alkalmazni, a P-értékeket csak iránymutatásként szabad felhasználni, és az eredményeket előzetesnek kell tekinteni, amíg a későbbi vizsgálatok nem erősítik meg azokat. Hasznos útmutató a Bonferroni-korrekció használata, amely egyszerűen azt állítja, hogy ha n független hipotézist tesztelünk, akkor 0,05 / n szignifikanciaszintet kell használnunk. Tehát ha két független hipotézis lenne, akkor az eredmény csak akkor lenne szignifikáns, ha P < 0,025. Vegye figyelembe, hogy mivel a tesztek ritkán függetlenek, ez egy nagyon konzervatív eljárás – azaz nem valószínű, hogy elutasítja a nullhipotézist. A nyomozónak akkor azt kellene megkérdeznie, hogy “függetlenek-e az adatok?” Ezt nehéz lehet eldönteni, de az ökölszabály szerint ugyanazon egyén vagy egyező egyének eredményei nem függetlenek. Így egy crossover vizsgálat eredménye, vagy egy eset-kontroll vizsgálat eredménye, amelyben a kontrollokat életkor, nem és társadalmi osztály szerint illesztették az esetekhez, nem függetlenek.

• Az elemzésnek tükröznie kell a tervet , és ezért az illesztett tervezést egyeztetett elemzésnek kell követnie.
• Az idővel mért eredmények különös gondosságot igényelnek. A statisztikai elemzés egyik leggyakoribb hibája a korrelált változók kezelése, mintha azok függetlenek lennének. Tegyük fel például, hogy a lábfekélyek kezelését vizsgáltuk, amelynek során egyeseknél mindkét lábukon fekély volt. Lehet, hogy 20 olyan alanyunk van, akinek 30 fekélye van, de a független információk száma 20, mert az egyes lábak fekélyeinek állapotát egy személy befolyásolhatja a személy egészségi állapota és egy elemzés, a fekélyeket független megfigyelésekként tévesnek tartotta. A vegyes párosított és párosítatlan
  adatok helyes elemzéséhez forduljon statisztikához.

A következő kérdés az, hogy “milyen típusú adatokat mérnek?” Az alkalmazott tesztet az adatok alapján kell meghatározni. Az egyeztetett vagy párosított adatok tesztválasztását az 1. táblázat, a független adatok pedig a 2. táblázatban mutatják be.

1. táblázat Statisztikai teszt választása párosított vagy egyeztetett megfigyelésből

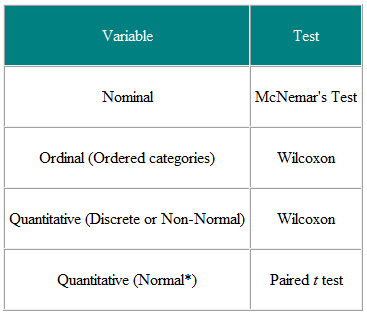
Hasznos eldönteni a bemeneti és az eredményváltozókat. Például egy klinikai vizsgálatban az input változó a kezelés típusa – egy nominális változó -, és az eredmény valamilyen klinikai mérőszám lehet, esetleg normálisan elosztva. A szükséges teszt ekkor a t-teszt (2. táblázat). Ha azonban az input változó folyamatos, mondjuk klinikai pontszám, és az eredmény nominális, mondjuk gyógyult vagy nem gyógyult, akkor a logisztikai regresszió szükséges elemzés. A t-teszt ebben az esetben segíthet, de nem adná meg nekünk azt, amire szükségünk van, nevezetesen a gyógyulás valószínűségét a klinikai pontszám adott értékére. Másik példaként tegyük fel, hogy van egy keresztmetszeti vizsgálatunk, amelynek során egy véletlenszerű mintát kérdezünk az emberektől, hogy szerintük háziorvosuk jó munkát végez-e, ötfokú skálán, és szeretnénk meggyőződni arról, hogy a nők véleménye magasabb-e mint a férfiak. Az input változó a gender, amely nominális. Az eredményváltozó az ötpontos rendes skála. Minden ember véleménye független a többitől, ezért független adatokkal rendelkezünk. A 2. táblázatból trend2 tesztet kell használnunk a trendre, vagy egy Mann-Whitney U tesztet a korrekcióra a kapcsolatokra (NB egy döntetlen akkor fordul elő, amikor kettő vagy több az értékek megegyeznek, ezért nincs szigorúan növekvő rangsorrend – ahol ez megtörténik, átlagolhatjuk a kötött értékek rangját). Megjegyzés: ha azonban egyesek háziorvossal osztoznak, mások pedig nem, akkor az adatok nem független és kifinomultabb elemzésre van szükség. Ne feledje, hogy ezeket a táblázatokat csak útmutatónak kell tekinteni, és minden egyes esetet érdemben kell figyelembe venni.

2. táblázat: Statisztikai teszt megválasztása független megfigyelésekhez

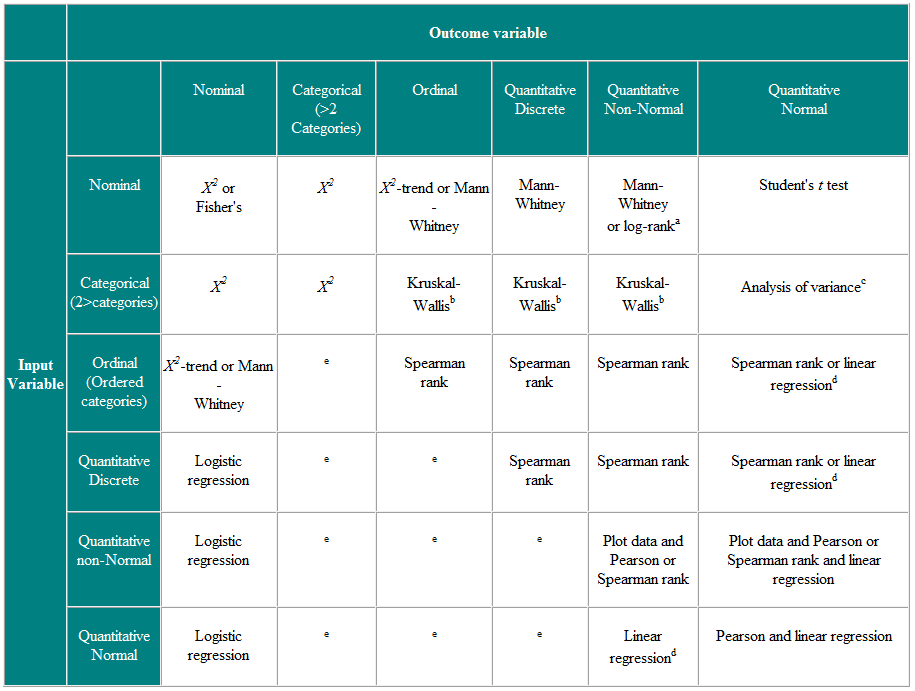
a Ha az adatokat cenzúrázzák. b A Kruskal-Wallis tesztet kétnél több csoport ordinális vagy nem normális változóinak összehasonlítására használják, és ez a Mann-Whitney U teszt általánosítása. c A varianciaanalízis általános technika, és egy változat (egyirányú varianciaanalízis) két vagy több csoport normálisan elosztott változók összehasonlítására szolgál, és ez a Kruskal-Wallistest paraméteres megfelelője. d Ha az eredményváltozó a függő változó, akkor feltéve, hogy a maradványok (a megfigyelt értékek és a regresszióból előre jelzett válaszok közötti különbségek) hihetően normálisan oszlanak meg, akkor a független változó eloszlása nem fontos. e Számos fejlettebb technika létezik, például Poisson regresszió ezeknek a helyzeteknek a kezelésére. Ehhez azonban bizonyos feltételezésekre van szükség, és gyakran könnyebb vagy kiosztani az eredményváltozót, vagy folytonosként kezelni.

A paraméteres tesztek azok, amelyek feltételezéseket tesznek a populáció eloszlásának paramétereiről, amelyekből a minta származik. . Ez gyakran az a feltételezés, hogy a népességi adatok normálisan oszlanak meg. A nem parametrikus tesztek “eloszlástól mentesek”, és mint ilyenek, használhatók nem normális változókhoz is. A 3. táblázat számos paraméteres teszt nem paraméteres megfelelőjét mutatja.

3. táblázat Paraméteres és Nem parametrikus tesztek két vagy több csoport összehasonlítására

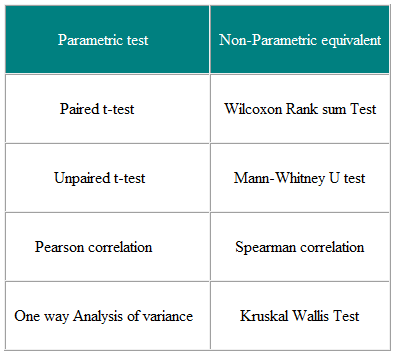
A nem parametrikus tesztek érvényesek mind a nem normálisan elosztott adatokra, mind a Normálisan elosztott adatok, miért ne használhatná mindig őket?

Körültekintőnek tűnik minden esetben nem parametrikus tesztek használata, ami megtakarítaná a Normality tesztelésével járó fáradságot. A paraméteres teszteket előnyben részesítjük, azonban a következő okokból:

1. Ritkán érdekel csupán egy szignifikancia-teszt; szeretnénk mondani valamit arról a populációról, amelyből a minták származnak, és ezt a legjobban

a paraméterek és a konfidencia intervallumok becslése.

2. Nehéz rugalmas modellezést végezni nem parametrikus tesztekkel, például zavaró tényezők megengedésével többszörös felhasználásával visszafejlődés.

3. A paraméteres tesztek általában nagyobb statisztikai erővel bírnak, mint nem-paraméteres ekvivalenseik. Más szavakkal, nagyobb valószínűséggel észlelhet jelentős különbségeket, ha azok valóban léteznek.

A nem parametrikus tesztek összehasonlítják a mediánokat?

Általánosan elterjedt vélekedés, hogy egy A Mann-Whitney U teszt valójában a mediánok közötti különbségek tesztje. Két csoportnak ugyanakkora mediánja lehet, és mégis jelentős Mann-Whitney U tesztet végezhet. Tekintsük a következő adatokat két csoportra, mindegyik 100 megfigyeléssel. 1. csoport: 98 (0), 1, 2; 2. csoport: 51 (0), 1, 48 (2). A medián mindkét esetben 0, de a Mann-Whitney-teszt alapján P < 0,0001. Csak akkor vagyunk képesek arra a feltételezésre, hogy a két csoportban a különbség egyszerűen egy helyváltozás (vagyis az adatok egyik csoportban történő eloszlása egyszerűen fix összeggel eltolódik a másiktól), akkor azt mondhatjuk, hogy a teszt a mediánok különbségének tesztje. Ha azonban a csoportok megoszlása azonos, akkor a helyváltozás ugyanolyan mértékben mozgatja a mediánokat és az eszközöket, így a mediánok különbsége megegyezik az átlagok különbségével. Így a Mann-Whitney U teszt az átlagok különbségének tesztje is. Hogyan kapcsolódik a Mann-Whitney U teszt a t-próbához? Ha egy két mintás t-teszt programba be kellene adni az adatok sorait, nem pedig magukat az adatokat, a kapott P-érték nagyon közel lenne a Mann-Whitney U-teszt eredményéhez.