Erőszámítások

Az erő nyomja vagy húzza.
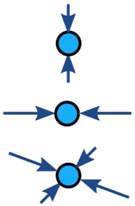
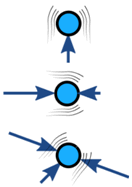
Az objektumon lévő erők általában kiegyensúlyozottak (ha kiegyensúlyozatlan, az objektum gyorsul):
 |
 |
|
| Kiegyensúlyozott | Kiegyensúlyozatlan | |
|---|---|---|
| Nincs gyorsulás | Gyorsulás |
Példa: A hídtorony tetején lévő erők egyensúlyban vannak (nem gyorsul):

A kábelek egyformán lefelé húzódnak balra és jobbra, és ezt a torony felfelé tolása egyensúlyozza. (A torony tolja? Igen! Képzelje el, hogy ott áll a torony helyett.) p>
Ilyen erőket modellezhetünk:

És amikor tegye őket fejhátig, és látjuk, hogy visszahúzódnak magukba, vagyis a nettó hatás nulla:

Az erők egyensúlyban vannak.
Állítólag az egyensúlyban lévő erők egyensúlyban vannak: a mozgásban szintén nincs változás.
Szabad testdiagramok
Az első lépés: szabad testdiagram (más néven erődiagram) rajzolása
Ingyenes testdiagram: olyan vázlat, ahol egy testet leválasztanak a világtól, kivéve a rá ható erőket.
A híd példában a torony tetejének szabad testdiagramja a következő:

Ingyenes testdiagram
Segít tisztán gondolkodjunk a testre ható erőkön.
Példa: Autó autópályán
Milyen erők vannak egy autópályán cirkáló autóban?

A motor keményen dolgozik, akkor miért nem gyorsul tovább az autó?
Mivel a vezetés az erőt kiegyensúlyozza:
- Légellenállás (leegyszerűsítve: th e a levegő ellenáll a körbetolódásnak),
- gördülési ellenállás, amelyet gördülősúrlódásnak is neveznek (a gumiabroncsok ellenállnak az alakjuk megváltozásának)

Ingyenes karosszériarajz
W az autó súlya,
R1 és R2 a gumiabroncsok gördülési ellenállása,
Az N1 és N2 a reakcióerő (kiegyenlíti az autó súlyát).
Megjegyzés: az acél kerekeknek (mint a vonatokon is) kisebb a gördülési ellenállása, de az úton túl csúszósak!
Számítások
Az erő vektor. A vektor nagysága (mérete) és iránya:

Az erőket úgy modellezhetjük, hogy megfelelő méretű és irányú nyilakat rajzolunk . Így:
Példa: A kilátás megcsodálása
Brady egy erkély szélén áll, amelyet vízszintes gerenda és támasz támaszt meg:

Súlya 80 kg.
Milyen erők vannak?
Vegyük azt a helyet, ahol áll, és gondolkodjunk az éppen ott lévő erőkön:

Súlya
80 kg-os tömege lefelé irányuló erőt hoz létre a gravitáció miatt.
Az erő a tömeg és a gyorsulás szorzata: F = ma
A gravitáció miatti gyorsulás a Földön 9,81 m / s2 , tehát a = 9,81 m / s2
F = 80 kg × 9,81 m / s2
F = 785 N
A többi erő
Az erők kiegyensúlyozottak, ezért vissza kell zárkózniuk magukhoz:

Trigonometria segítségével megoldhatjuk .
Mivel ez egy derékszögű háromszög, ezért a SOHCAHTOA segít.
A Sugár számára ismerjük a szomszédosakat, szeretnénk ismerni az Ellentétet, és a „TOA” azt mondja, hogy használjuk a Tangentet:
barnás (60 ° ) = Sugár / 785 N
Sugár / 785 N = barnás (60 °)
Sugár = barnás (60 °) × 785 N
Sugár = 1.732 … × 785 N = 1360 N
A Strut esetében ismerjük a szomszédosokat, meg akarjuk ismerni a Hypotenuse-t, és a “CAH” azt mondja, hogy használjuk a Cosine-t:
cos (60 °) = 785 N / Strut
Strut × cos (60 °) = 785 N
Strut = 785 N / cos (60 °)
Strut = 785 N / 0,5 = 1570 N
Megoldva:

Érdekes, hogy mekkora erő van a gerenda és a támasz a megtámogatott súlyhoz képest!
Nyomaték (vagy pillanat)
Mi van, ha a gerenda csak a falba van ragasztva (konzolnak hívják)?

Nincs támasztórúd, akkor mi történik az erőkkel?
A szabad test diagram így néz ki:

Az R felfelé irányuló erő kiegyenlíti a lefelé eső súlyt.
Csak ezzel a kettővel erők a sugár úgy forog, mint a propeller! De van egy “fordulóhatás” M is, a Moment (vagy Nyomaték) nevű, amely kiegyenlíti:
Moment: Az erő szoros szögben szorozza meg a távolságot.
Tudjuk, hogy a súly 785 N, és tudnunk kell a derékszögben mért távolságot is, amely ebben az esetben 3,2 m.
M = 785 N x 3,2 m = 2512 Nm
És ez a pillanat az akadályozza meg a gerenda forgását.

A horgászbotra kapaszkodva pillanatot érezhet.
A súlya megtartása mellett meg kell akadályoznia a lefelé történő forgást.
Súrlódás
Doboz a rámpán
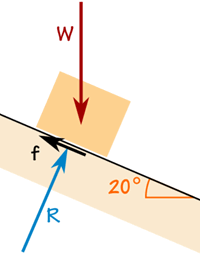
A doboz súlya 100 kg.
A súrlódási erő elegendő ahhoz, hogy ott tartsa, ahol van.
Az R reakcióerő merőleges a rámpa.
A doboz nem gyorsul, ezért az erők egyensúlyban vannak:
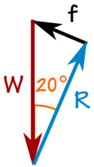
A 100 kg tömeg a lefelé irányuló erőt hozza létre a gravitáció miatt:
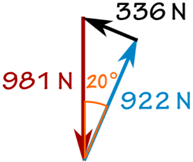
W = 100 kg × 9,81 m / s2 = 981 N
A háromszög megoldására SOHCAHTOA-t használhatunk.
súrlódás f:
sin (20 °) = f / 981 N
f = sin (20 °) × 981 N = 336 N
Reakció N:
cos (20 °) = R / 981 N
R = cos (20 °) × 981 N = 922 N
És ezt kapjuk:
Tippek a szabad testdiagramok rajzolásához
- Rajzolj a lehető legegyszerűbben. Egy doboz gyakran elég jó.
- Az erők abba az irányba mutatnak, ahol a testre hatnak
- egyenes nyilak az erők számára
- ívelt nyilak pillanatokra
Sam és Alex húzzon egy dobozt
A számítások olykor könnyebbek lehetnek, ha a nagyságot és az irányt x-be és y-be változtatjuk:
 |
< = > |  |
| A vektor a Polar koordinátákban |
Vektor a derékszögű koordináták |
A konvertálásról a Polar és a Cartesian oldalon olvashat. Koordinátorok, de itt van egy rövid összefoglaló:
Használjuk őket!