• A K-Legközelebbi szomszéd az egyik legegyszerűbb gépi tanulási algoritmus a felügyelt tanulási technikáról.
• A K-NN algoritmus feltételezi az új eset / adatok és a rendelkezésre álló esetek hasonlóságát, és az új esetet abba a kategóriába sorolja, amely a legjobban hasonlít az elérhető kategóriákra.
• K-NN algoritmus tárolja az összes rendelkezésre álló adatot, és a hasonlóság alapján új osztályozási pontot osztályoz. Ez azt jelenti, hogy amikor új adatok jelennek meg, akkor a K-NN algoritmus segítségével könnyen besorolhatók kútkategóriába.
• A K-NN algoritmus használható a regresszióhoz, valamint az osztályozáshoz, de leginkább az osztályozási problémákhoz.
• A K-NN egy nem paraméteres algoritmus, ami azt jelenti, nem tesz feltételezést az alapul szolgáló adatokról.
• Lusta tanuló algoritmusnak is nevezik, mert nem azonnal tanul a képzési halmazból, hanem tárolja az adatkészletet, és a besoroláskor végrehajt egy művelet az adatkészleten.
• A KNN algoritmus a képzési szakaszban csak tárolja az adatkészletet, és amikor új adatokhoz jut, akkor ezeket az adatokat egy olyan kategóriába sorolja, amely nagyon hasonlít az új adatokhoz.
• Példa: Tegyük fel, hogy van egy képünk egy lényről, amely hasonlít a macskához és a kutyához, de szeretnénk tudni, hogy ez macska vagy kutya. Tehát ehhez az azonosításhoz használhatjuk a KNN algoritmust, mivel ez hasonlósági mérőn működik. KNN modellünk megtalálja az új adatkészlet hasonló jellemzőit a macskák és kutyák képeihez, és a leginkább hasonló jellemzők alapján macskák vagy kutyák kategóriájába sorolja.

Miért van szükségünk K-NN algoritmusra?

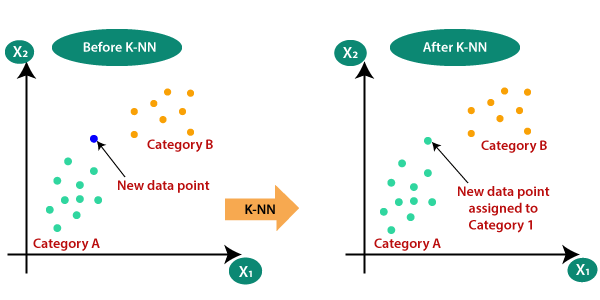
Tegyük fel, hogy két kategória létezik, azaz A és B kategória, és új x1 adatpontunk van, tehát ez az adatpont e kategóriák közül melyikben rejlik. Az ilyen típusú problémák megoldásához K-NN algoritmusra van szükségünk. A K-NN segítségével könnyen azonosíthatjuk egy adott adatkészlet kategóriáját vagy osztályát. Vegye figyelembe az alábbi ábrát:

Hogyan működik a K-NN?

A K-NN működése magyarázható az alábbi algoritmus:

• 1. lépés: Válassza ki a szomszédok K számát
• 2. lépés: Számítsa ki a szomszédok K számának euklideszi távolságát
• 3. lépés: Vegyük a K legközelebbi szomszédokat a számított euklideszi távolság szerint.
• 4. lépés: E k szomszédok között számoljuk meg az egyes kategóriák adatpontjainak számát.
• 5. lépés: Rendelje hozzá az új adatpontokat ahhoz a kategóriához, amelyhez a szomszéd maximális száma tartozik.
• 6. lépés: Készen áll a modellünk.

Tegyük fel, hogy új adatpontunk van, és a szükséges kategóriába kell sorolnunk. Tekintsük az alábbi képet:

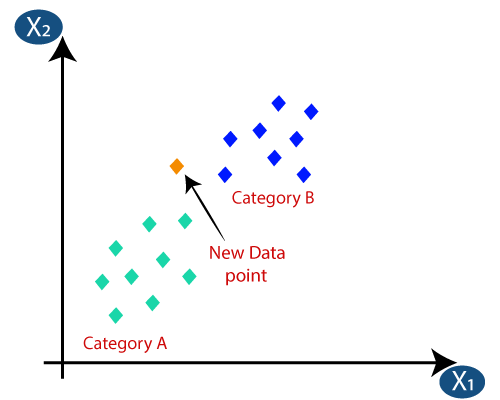
• Először a szomszédok számát választjuk meg, így a k = 5 értéket fogjuk választani.
• Ezután kiszámítjuk az adatpontok közötti euklideszi távolságot. Az euklideszi távolság két pont közötti távolság, amelyet a geometriában már tanulmányoztunk. Kiszámítható:

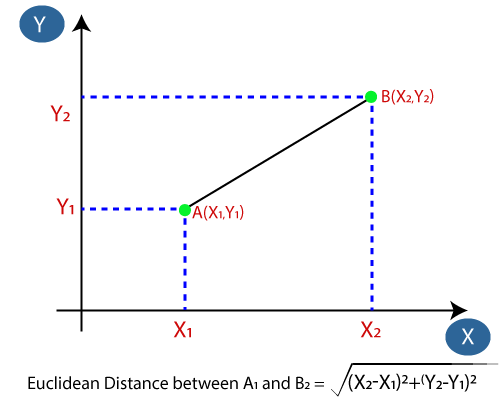
• Az euklideszi távolság kiszámításával megkaptuk a legközelebbi szomszédokat, három legközelebbi szomszédként az A kategóriában és két legközelebbi szomszéd a B kategóriában. Vegye figyelembe az alábbi képet:

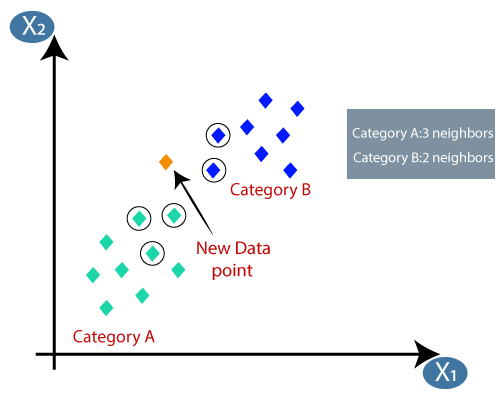
• Mint láthatjuk, a 3 legközelebbi szomszéd a kategóriából származik A, ezért ennek az új adatpontnak az A kategóriába kell tartoznia.

Hogyan válasszuk ki a K értékét a K-NN algoritmusban?

Az alábbiakban néhány pont található ne feledje, miközben kiválasztja a K értékét a K-NN algoritmusban:

• A “K” legjobb értékének meghatározására nincs különösebb módszer, ezért néhány értéket ki kell próbálnunk a legjobb megtalálásához. belőlük. A K számára a legelőnyösebb érték az 5.
• A K nagyon alacsony értéke, például a K = 1 vagy a K = 2, zajos lehet, és a modellben a kiugró értékek hatásához vezethet.
• A K nagy értékei jóak, de nehézségeket okozhatnak.

A KNN algoritmus előnyei:

• Egyszerű megvalósítani.
• Robusztus a zajos edzésadatokra
• Hatékonyabb lehet, ha az edzésadatok nagyok.

A KNN algoritmus hátrányai:

• Mindig meg kell határoznia a K értékét, amely valamikor összetett lehet.
• A számítási költség magas, mert az összes képzési minta adatpontjai közötti távolság kiszámításra kerül. .

A KNN algoritmus Python-megvalósítása

A K-NN algoritmus Python-megvalósításának elvégzéséhez ugyanazt a problémát és adatkészletet fogjuk használni Logisztikus regresszió. De itt javítani fogjuk a modell teljesítményét. Az alábbiakban a probléma leírása található:

Probléma a K-NN algoritmus számára: Van egy autógyártó cég, amely új terepjáró-autót gyártott.A vállalat azokat a felhasználókat szeretné megadni, akik érdeklődnek az adott terepjáró megvásárlása iránt. Tehát erre a problémára van egy olyan adatkészletünk, amely több felhasználói információt tartalmaz a közösségi hálózaton keresztül. Az adatkészlet sok információt tartalmaz, de a Becsült fizetés és életkor figyelembe vesszük a független változót, a Vásárolt változó pedig a függő változót. Az alábbiakban található az adatkészlet:

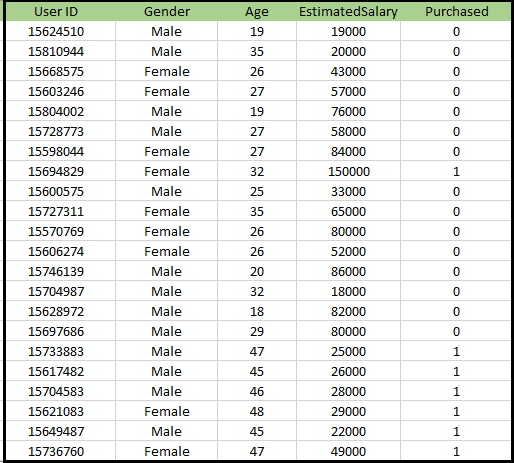
A K-NN algoritmus megvalósításának lépései:

• Adatok előkezelési lépése
• A K-NN algoritmus illesztése az edzéskészlethez
• A teszt eredményének megjósolása
• Az eredmény teszt pontossága (Confusion mátrix létrehozása)
• A tesztkészlet eredményének megjelenítése.

Adatok előfeldolgozási lépése:

Az adatok előkezelési lépése pontosan megegyezik a logisztikai regresszióval. Az alábbiakban látható a kód érte:

A fenti kód futtatásával az adatkészletet importáljuk a programunkba és jól előre feldolgozzuk. A szolgáltatás skálázása után a teszt adatkészletünk így fog kinézni:

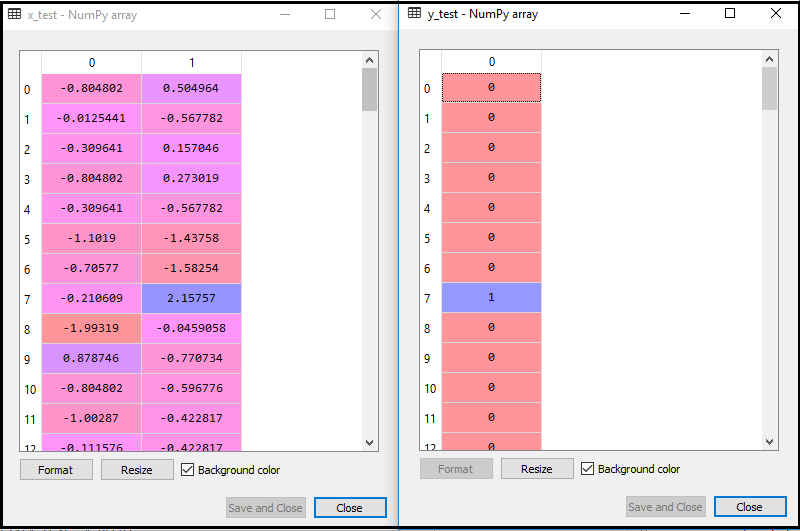
A fenti kimenetből im életkor, láthatjuk, hogy az adatainkat sikeresen méretezzük.

• A K-NN osztályozó illesztése az edzés adataihoz:
  Most a K-NN osztályozót illesztjük az edzés adataihoz. Ehhez importáljuk a Sklearn Neighbors könyvtár KNeighborsClassifier osztályát. Az osztály importálása után létrehozzuk az osztály Classifier objektumát. Ennek az osztálynak a paramétere
  • n_ szomszédok lesz: Az algoritmus szükséges szomszédjainak meghatározása. Általában ez 5-öt vesz igénybe.
  • metric = “minkowski”: Ez az alapértelmezett paraméter, és ez határozza meg a pontok közötti távolságot.
  • p = 2: Ez egyenértékű a standarddal Euklideszi metrika.

  És akkor illesztjük az osztályozót a képzési adatokhoz. Az alábbiakban található a kód:

Output: A fenti kód végrehajtásával a kimenetet a következő módon kapjuk meg:

• A teszt eredményének megjósolása: A tesztkészlet eredményének megjóslásához létrehozunk egy y_pred vektort, ahogy a logisztikai regresszióban tettük. Az alábbiakban található a kód:

Kimenet:

A fenti kód kimenete a következő lesz:

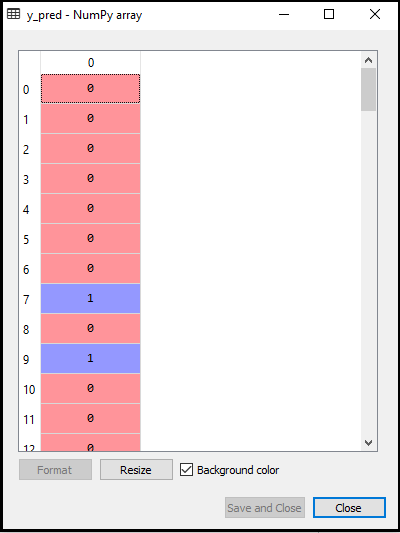
• A zavartsági mátrix létrehozása:
  Most létrehozzuk a K-NN modellünk zavartsági mátrixát, hogy lássuk az osztályozó pontosságát. Az alábbiakban látható a kód:

A fenti kódban importáltuk a confusion_matrix függvényt, és a cm változó segítségével hívtuk meg.

Kimenet: A fenti kód futtatásával megkapjuk az alábbiak szerinti mátrixot:

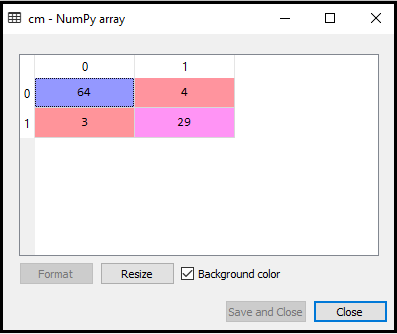
A fenti képen láthatjuk 64 + 29 = 93 helyes és 3 + 4 = 7 helytelen jóslat létezik, míg a Logisztikai regresszióban 11 helytelen jóslat volt. Tehát elmondhatjuk, hogy a modell teljesítménye javul a K-NN algoritmus használatával.

• A képzési halmaz eredményének megjelenítése:
  Most megjelenítjük a K edzéskészlet eredményét -NN modell. A kód ugyanaz marad, mint a Logisztikai regresszióban, kivéve a grafikon nevét. Az alábbiakban található a kód:

Kimenet:

A fenti kód végrehajtásával megkapjuk az alábbi grafikont:

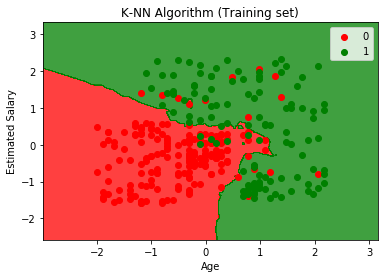
A kimeneti grafikon eltér attól a gráftól, amelyet a logisztikai regresszió során tapasztaltunk. Ez az alábbi pontokban érthető meg:

• Amint láthatjuk, a grafikon a piros és a zöld pontokat mutatja. A zöld pontok a Megvásárolt (1) és a Vörös pontok a nem megvásárolt (0) változóra vonatkoznak.
• A grafikon szabálytalan határt mutat, ahelyett, hogy bármilyen egyeneset vagy görbét mutatna, mert ez egy K-NN algoritmus, vagyis a legközelebbi szomszéd megtalálása.
• A grafikon a felhasználókat a megfelelő kategóriákba sorolta, mivel azoknak a felhasználóknak a többsége, akik nem vásárolták meg a terepjárót, a vörös, míg a terepjárót vásárló felhasználók a zöld régióban vannak.
• A grafikon jó eredményt mutat, de mégis vannak zöld pontok a piros régióban és a piros pontok a zöld régióban. De ez nem nagy kérdés, mivel ezzel a modellel megakadályozható a túlillesztés.
• Ennélfogva modellünk jól képzett.
• A tesztkészlet eredményének megjelenítése:
  A modell oktatása után most egy új adatkészlet, azaz Tesztadatkészlet. A kód változatlan, néhány kisebb változtatást leszámítva: például az x_train és az y_train helyébe az x_test és az y_test lép.
  Az alábbiakban látható a kód:

Kimenet:

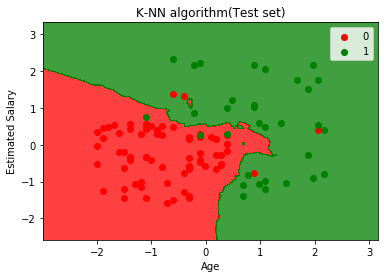
A fenti grafikon a teszt adatkészlet kimenetét mutatja. Amint a grafikonon láthatjuk, az előrejelzett kimenet jól jó, mivel a piros pontok többsége a vörös régióban van, ill a zöld pontok többsége a zöld régióban található.

A vörös régióban azonban kevés zöld, a zöld régióban pedig néhány piros pont található. Tehát ezek a helytelen megfigyelések, amelyeket megfigyeltünk a zavaros mátrixban (7 Helytelen kimenet).