Egy diszkrét véletlen változó eloszlásának meghatározásához megadhatjuk annak PMF-jét vagy CDF-jét. Folyamatos véletlen változók esetén a CDF jól definiált, így megadhatjuk a CDF-et. A PMF azonban nem működik folyamatos véletlenszerű változók esetén, mert egy folytonos véletlen változó esetén $ P (X = x) = 0 $ minden $ x \ in \ mathbb {R} $ esetén. Ehelyett általában meghatározhatjuk a valószínűségi sűrűség függvényt (PDF). A PDF a valószínűség sűrűsége, nem pedig a valószínűség tömege. A koncepció nagyon hasonlít a fizika tömegsűrűségéhez: egysége az egységnyi hosszúságra eső valószínűség. Ahhoz, hogy megismerje a PDF fájlt, vegyen fontolóra egy folyamatos véletlen változót: $ X $, és a következőképpen határozza meg az $ f_X (x) $ függvényt (bárhol is van a határ): $$ f_X (x) = \ lim _ {\ Delta \ rightarrow 0 ^ +} \ frac {P (x

$$ f_X (x) = \ lim _ {\ Delta \ rightarrow 0} \ frac {F_X (x + \ Delta) -F_X (x)} {\ Delta} $$ $$ = \ frac {dF_X (x)} {dx} = F ” _X (x), \ hspace {20pt} \ textrm {if} Az F_X (x) \ textrm {a} x. $$

alapján megkülönböztethető. Így a következő definícióval rendelkezünk: Folyamatos véletlen változók PDF-fájlja:

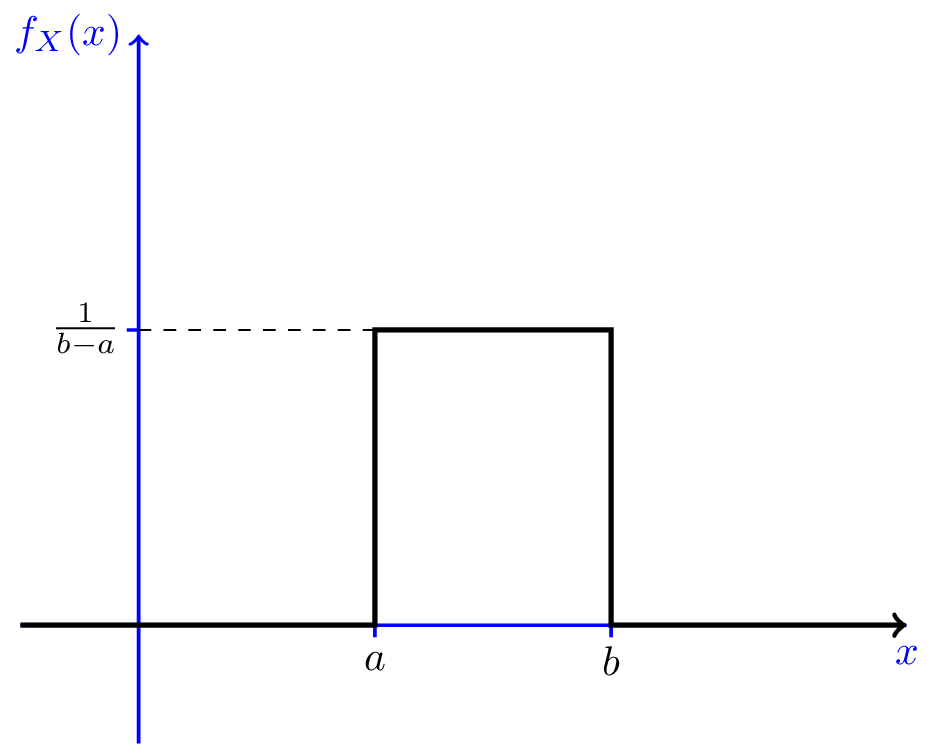
Példa
Legyen $ X $ folyamatos véletlen változó a következő PDF-del \ begin {equation} \ nonumber f_X (x) = \ left \ {\ begin {tömb} {ll} ce ^ {- x} & \ quad x \ geq 0 \\ 0 & \ quad \ text {különben} \ end {tömb} \ right. \ end {egyenlet} ahol $ c $ pozitív konstans.

1. Keresse meg a $ c $ értéket.
2. Keresse meg az X CDF értékét, $ F_X (x) $.
3. Keresse meg a $ P (1

Tartomány