Calcoli della forza

La forza è push o pull.
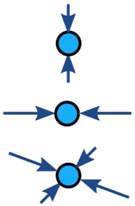
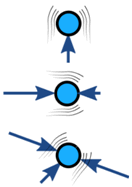
Le forze su un oggetto sono generalmente bilanciate (se sbilanciate l’oggetto accelera):
 |
 |
|
| Bilanciato | Non bilanciato | |
|---|---|---|
| Nessuna accelerazione | Accelerazione |
Esempio: le forze in cima a questa torre del ponte sono in equilibrio (non sta accelerando):

I cavi tirano verso il basso equamente a sinistra ea destra, e questo è bilanciato dalla spinta verso l’alto della torre. (La torre spinge? Sì! Immagina di stare lì invece della torre.)
Possiamo modellare le forze in questo modo:

E quando noi mettendoli testa a coda vediamo che si chiudono su se stessi, il che significa che l’effetto netto è zero:

Le forze sono in equilibrio.
Si dice che le forze in equilibrio siano in equilibrio: non vi è alcun cambiamento nel movimento.
Diagrammi a corpo libero
Il primo passo è per disegnare un diagramma del corpo libero (chiamato anche diagramma della forza)
Diagramma del corpo libero: uno schizzo in cui un corpo è tagliato libero dal mondo tranne che per le forze che agiscono su di esso.
Nell’esempio del ponte il diagramma del corpo libero per la parte superiore della torre è:

Diagramma del corpo libero
Aiuta pensare chiaramente alle forze che agiscono sul corpo.
Esempio: auto su un’autostrada
Quali sono le forze su un’auto che percorre l’autostrada?

Il motore sta lavorando sodo, quindi perché l’auto non continua ad accelerare?
Perché la guida la forza è bilanciata da:
- Resistenza dell’aria (in parole semplici: th L’aria resiste a essere spinta in giro),
- Resistenza al rotolamento, chiamata anche attrito di rotolamento (i pneumatici resistono alla modifica della loro forma)

Diagramma del corpo libero
W è il peso dell’auto,
R1 e R2 sono la resistenza al rotolamento degli pneumatici,
N1 e N2 sono le forze di reazione (bilanciare il peso dell’auto).
Nota: le ruote in acciaio (come sui treni) hanno meno resistenza al rotolamento, ma sono troppo scivolose sulla strada!
Calcoli
La forza è un vettore. Un vettore ha grandezza (dimensione) e direzione:

Possiamo modellare le forze disegnando frecce della dimensione e della direzione corrette . In questo modo:
Esempio: ammirare il panorama
Brady si trova sul bordo di un balcone sostenuto da una trave orizzontale e da un montante:

Pesa 80 kg.
Quali sono le forze?
Prendiamo il punto in cui si trova e pensiamo alle forze che stanno lì:

Il suo peso
La sua massa di 80 kg crea una forza verso il basso dovuta alla gravità.
La forza è l’accelerazione della massa moltiplicata per: F = ma
L’accelerazione dovuta alla gravità sulla Terra è di 9,81 m / s2 , quindi a = 9,81 m / s2
F = 80 kg × 9,81 m / s2
F = 785 N
Le altre forze
Le forze sono bilanciate, quindi dovrebbero chiudersi su se stesse in questo modo:

Possiamo usare la trigonometria per risolverlo .
Poiché si tratta di un triangolo rettangolo, SOHCAHTOA aiuterà.
Per il raggio, conosciamo l’adiacente, vogliamo conoscere l’opposto e “TOA” ci dice di usare tangente:
abbronzatura (60 ° ) = Fascio / 785 N
Fascio / 785 N = tan (60 °)
Fascio = tan (60 °) × 785 N
Fascio = 1,732 … × 785 N = 1360 N
Per lo Strut, conosciamo l’adiacente, vogliamo conoscere l’ipotenusa e “CAH” ci dice di usare il coseno:
cos (60 °) = 785 N / puntone
puntone × cos (60 °) = 785 N
puntone = 785 N / cos (60 °)
Strut = 785 N / 0,5 = 1570 N
Risolto:

Interessante quanta forza è applicata la trave e il montante rispetto al peso supportato!
Coppia (o momento)
Cosa succede se la trave è semplicemente conficcata nel muro (chiamato cantilever)?

Non ci sono montanti di sostegno, quindi cosa succede alle forze?
Diagramma del corpo libero ha questo aspetto:

La forza verso l’alto R bilancia il Peso verso il basso.
Con solo questi due forza il raggio ruoterà come un’elica! Ma esiste anche un “effetto virata” M chiamato Momento (o Coppia) che lo bilancia:
Momento: la forza moltiplicata per la distanza ad angolo retto.
Sappiamo che il peso è 785 N, e dobbiamo anche conoscere la distanza ad angolo retto, che in questo caso è 3,2 m.
M = 785 N x 3,2 m = 2512 Nm
E quel momento è ciò che impedisce al raggio di ruotare.

Puoi sentire il momento quando tieni una canna da pesca.
Oltre a sostenerne il peso, devi impedirne la rotazione verso il basso.
Friction
Box su una rampa
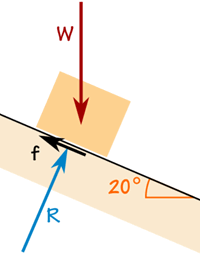
La scatola pesa 100 kg.
La forza di attrito è sufficiente per mantenerla dov’è.
La forza di reazione R è ad angolo retto rispetto al rampa.
La scatola non sta accelerando, quindi le forze sono in equilibrio:
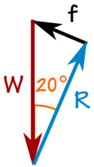
Il 100 kg di massa crea una forza verso il basso dovuta alla gravità:
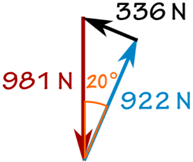
W = 100 kg × 9,81 m / s2 = 981 N
Possiamo usare SOHCAHTOA per risolvere il triangolo.
Attrito f:
sin (20 °) = f / 981 N
f = sin (20 °) × 981 N = 336 N
Reazione N:
cos (20 °) = R / 981 N
R = cos (20 °) × 981 N = 922 N
E otteniamo:
Suggerimenti per disegnare diagrammi a corpo libero
- Disegna nel modo più semplice possibile. Una scatola è spesso abbastanza buona.
- Le forze puntano nella direzione in cui agiscono sul corpo
- frecce diritte per forze
- frecce curve per momenti
Sam e Alex tirano una scatola
A volte i calcoli possono essere più facili quando trasformiamo la grandezza e la direzione in x e y:
 |
< = > |  |
| Vettore a nelle coordinate polari |
Vettore a in coordinate cartesiane |
Puoi leggere come convertirle in polari e cartesiani Coordinate, ma ecco un breve riassunto:
Usiamole!