Test parametrici e non parametrici per confrontare due o più gruppi

Statistiche: test parametrici e non parametrici

Questa sezione copre:

• Scelta di un test
• Test parametrici
• Test non parametrici

Scelta di un test

In termini di selezione di un test statistico, la domanda più importante è “qual è l’ipotesi principale dello studio?” In alcuni casi non ci sono ipotesi; l’investigatore vuole solo “vedere cosa c’è”. Ad esempio, in uno studio sulla prevalenza non ci sono ipotesi da testare e la dimensione dello studio è determinata dall’accuratezza con cui lo sperimentatore vuole determinare la prevalenza. Se non ci sono ipotesi, non ci sono test statistici. È importante decidere a priori quali ipotesi sono confermative (cioè stanno testando una relazione presupposta) e quali sono esplorative (sono suggerite dai dati). Nessun singolo studio può supportare un’intera serie di ipotesi. Un piano sensato è limitare fortemente il numero di ipotesi di conferma. Sebbene sia valido utilizzare test statistici su ipotesi suggerite dai dati, i valori di P dovrebbero essere usati solo come linee guida e i risultati trattati come provvisori fino a conferma da studi successivi. Una guida utile è usare una correzione Bonferroni, che afferma semplicemente che se si stanno verificando n ipotesi indipendenti, si dovrebbe usare un livello di significatività di 0,05 / n. Quindi se ci fossero due ipotesi indipendenti un risultato sarebbe dichiarato significativo solo se P < 0,025. Si noti che, poiché i test sono raramente indipendenti, questa è una procedura molto conservativa, ovvero una che è improbabile che rifiuti l’ipotesi nulla. L’investigatore dovrebbe quindi chiedere “i dati sono indipendenti?” Questo può essere difficile da decidere, ma come regola pratica i risultati sullo stesso individuo, o su individui abbinati, non sono indipendenti. Pertanto i risultati di uno studio crossover o di uno studio caso-controllo in cui i controlli sono stati abbinati ai casi per età, sesso e classe sociale, non sono indipendenti.

• L’analisi dovrebbe riflettere il disegno e quindi un progetto abbinato dovrebbe essere seguito da un’analisi abbinata.
• I risultati misurati nel tempo richiedono un’attenzione particolare. Uno degli errori più comuni nell’analisi statistica è trattare le variabili correlate come se fossero
  indipendenti. Ad esempio, supponiamo che stessimo esaminando il trattamento delle ulcere alle gambe, in cui alcune persone avevano un’ulcera su ciascuna gamba. Potremmo avere 20 soggetti con
  30 ulcere, ma il numero di informazioni indipendenti è 20 perché lo stato delle ulcere su ciascuna gamba per una persona può essere influenzato dallo stato di salute
  della persona e da un’analisi che considerare le ulcere come osservazioni indipendenti non sarebbe corretto. Per un’analisi corretta dei dati
  accoppiati e non accoppiati, consultare uno statistico.

La domanda successiva è “quali tipi di dati vengono misurati?” Il test utilizzato dovrebbe essere determinato dai dati. La scelta del test per i dati abbinati o accoppiati è descritta nella Tabella 1 e per i dati indipendenti nella Tabella 2.

Tabella 1 Scelta del test statistico dall’osservazione accoppiata o accoppiata

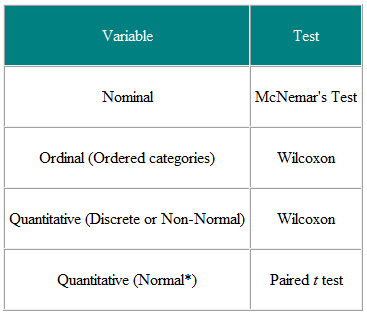
È utile decidere le variabili di input e le variabili di risultato. Ad esempio, in uno studio clinico la variabile di input è il tipo di trattamento – una variabile nominale – e il risultato può essere una misura clinica forse normalmente distribuita. Il test richiesto è quindi il test t (Tabella 2). Tuttavia, se la variabile di input è continua, ad esempio un punteggio clinico, e il risultato è nominale, ad esempio curato o non curato, la regressione logistica è l’analisi richiesta. Un test t in questo caso può aiutare ma non ci darebbe ciò di cui abbiamo bisogno, ovvero la probabilità di una cura per un dato valore del punteggio clinico. Come altro esempio, supponiamo di avere uno studio trasversale in cui chiediamo a un campione casuale di persone se pensano che il loro medico di base stia facendo un buon lavoro, su una scala di cinque punti, e desideriamo accertare se le donne hanno un’opinione più alta dei medici di base rispetto agli uomini. La variabile di input è il sesso, che è nominale. La variabile di risultato è la scala ordinale a cinque punti. L’opinione di ogni persona è indipendente dalle altre, quindi abbiamo dati indipendenti. Dalla tabella 2 dovremmo usare un test χ2 per il trend, o un test U di Mann-Whitney con una correzione per i legami (NB si verifica un pareggio dove due o più i valori sono gli stessi, quindi non esiste un ordine rigorosamente crescente dei ranghi – dove ciò accade, si può fare la media dei ranghi per valori pari). Nota, tuttavia, se alcune persone condividono un medico generico e altre no, i dati non lo sono è necessaria un’analisi indipendente e più sofisticata Si noti che queste tabelle dovrebbero essere considerate solo come guide e ogni caso dovrebbe essere considerato nel merito.

Tabella 2 Scelta del test statistico per osservazioni indipendenti

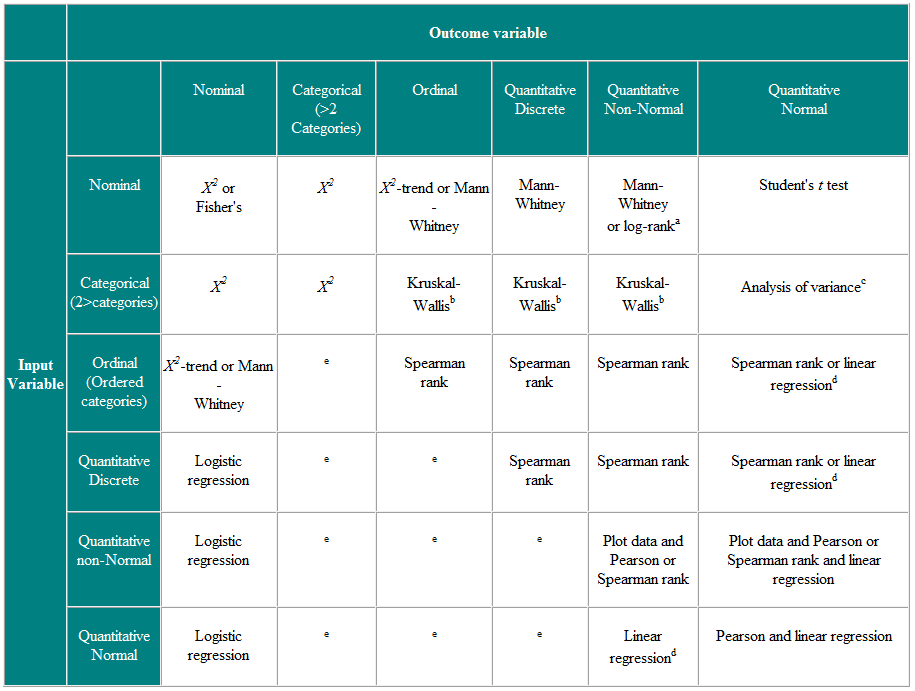
a Se i dati vengono censurati. b Il test di Kruskal-Wallis viene utilizzato per confrontare variabili ordinali o non normali per più di due gruppi ed è una generalizzazione del test U di Mann-Whitney. c L’analisi della varianza è una tecnica generale e una versione (analisi della varianza unidirezionale) viene utilizzata per confrontare le variabili normalmente distribuite per più di due gruppi ed è l’equivalente parametrico del Kruskal-Wallistest. d Se la variabile di risultato è la variabile dipendente, a condizione che i residui (le differenze tra i valori osservati e le risposte previste dalla regressione) siano distribuiti in modo plausibile Normalmente, la distribuzione della variabile indipendente non è importante. e Esistono numerose tecniche più avanzate, come la regressione di Poisson, per affrontare queste situazioni. Tuttavia, richiedono alcune ipotesi ed è spesso più facile o dicotomizzare la variabile di risultato o trattarla come continua.

I test parametrici sono quelli che fanno ipotesi sui parametri della distribuzione della popolazione da cui viene tratto il campione . Questo è spesso il presupposto che i dati sulla popolazione siano normalmente distribuiti. I test non parametrici sono “privi di distribuzione” e, come tali, possono essere utilizzati per variabili non normali. La Tabella 3 mostra l’equivalente non parametrico di una serie di test parametrici.

Tabella 3 Parametrico e Test non parametrici per il confronto di due o più gruppi

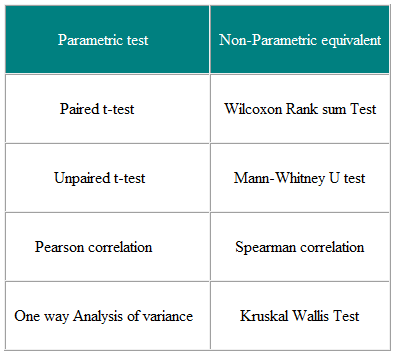
I test non parametrici sono validi sia per i dati non distribuiti normalmente sia per Dati normalmente distribuiti, quindi perché non usarli sempre?

Sembrerebbe prudente utilizzare test non parametrici in tutti i casi, il che risparmierebbe il fastidio di testare la normalità. I test parametrici sono preferiti, tuttavia, per i seguenti motivi:

1. Raramente siamo interessati a un test di significatività da solo; vorremmo dire qualcosa sulla popolazione da cui provengono i campioni, e questo è meglio farlo con
stime di parametri e intervalli di confidenza.

2. È difficile eseguire modelli flessibili con test non parametrici, ad esempio consentendo fattori di confusione utilizzando più regressione.

3. I test parametrici di solito hanno più potere statistico dei loro equivalenti non parametrici. In altre parole, è più probabile che si rilevino differenze significative quando
esistono veramente.

I test non parametrici confrontano le mediane?

È opinione comune che un Il test U di Mann-Whitney è infatti un test per le differenze nelle mediane. Tuttavia, due gruppi potrebbero avere la stessa mediana e tuttavia avere un significativo test U di Mann-Whitney. Considera i seguenti dati per due gruppi, ciascuno con 100 osservazioni. Gruppo 1: 98 (0), 1, 2; Gruppo 2:51 (0), 1, 48 (2). La mediana in entrambi i casi è 0, ma dal test di Mann-Whitney P < 0,0001. Solo se siamo pronti a fare l’ipotesi aggiuntiva che la differenza nei due gruppi sia semplicemente uno spostamento di posizione (ovvero, la distribuzione dei dati in un gruppo è semplicemente spostata di una quantità fissa dall’altro) possiamo dire che il test è un test della differenza di mediane. Tuttavia, se i gruppi hanno la stessa distribuzione, uno spostamento nella posizione sposterà le mediane e le medie della stessa quantità e quindi la differenza delle mediane è uguale alla differenza delle medie. Quindi il test U di Mann-Whitney è anche un test per la differenza di medie. In che modo il test U di Mann-Whitney è correlato al test t? Se si inserissero i ranghi dei dati anziché i dati stessi in un programma di test t a due campioni, il valore P ottenuto sarebbe molto vicino a quello prodotto da un test U di Mann-Whitney.