Per determinare la distribuzione di una variabile casuale discreta possiamo fornire il suo PMF o CDF. Per le variabili casuali continue, il CDF è ben definito, quindi possiamo fornire il CDF. Tuttavia, il PMF non funziona per variabili casuali continue, perché per una variabile casuale continua $ P (X = x) = 0 $ per tutti i $ x \ in \ mathbb {R} $. Invece, di solito possiamo definire la funzione di densità di probabilità (PDF). Il PDF è la densità di probabilità piuttosto che la massa di probabilità. Il concetto è molto simile alla densità di massa in fisica: la sua unità è la probabilità per unità di lunghezza. Per avere un’idea del PDF, considera una variabile casuale continua $ X $ e definisci la funzione $ f_X (x) $ come segue (ovunque esista il limite): $$ f_X (x) = \ lim _ {\ Delta \ rightarrow 0 ^ +} \ frac {P (x

$$ f_X (x) = \ lim _ {\ Delta \ rightarrow 0} \ frac {F_X (x + \ Delta) -F_X (x)} {\ Delta} $$ $$ = \ frac {dF_X (x)} {dx} = F ” _X (x), \ hspace {20pt} \ textrm {if} F_X (x) \ textrm {è derivabile in} x. $$

Quindi, abbiamo la seguente definizione per il PDF di variabili casuali continue:

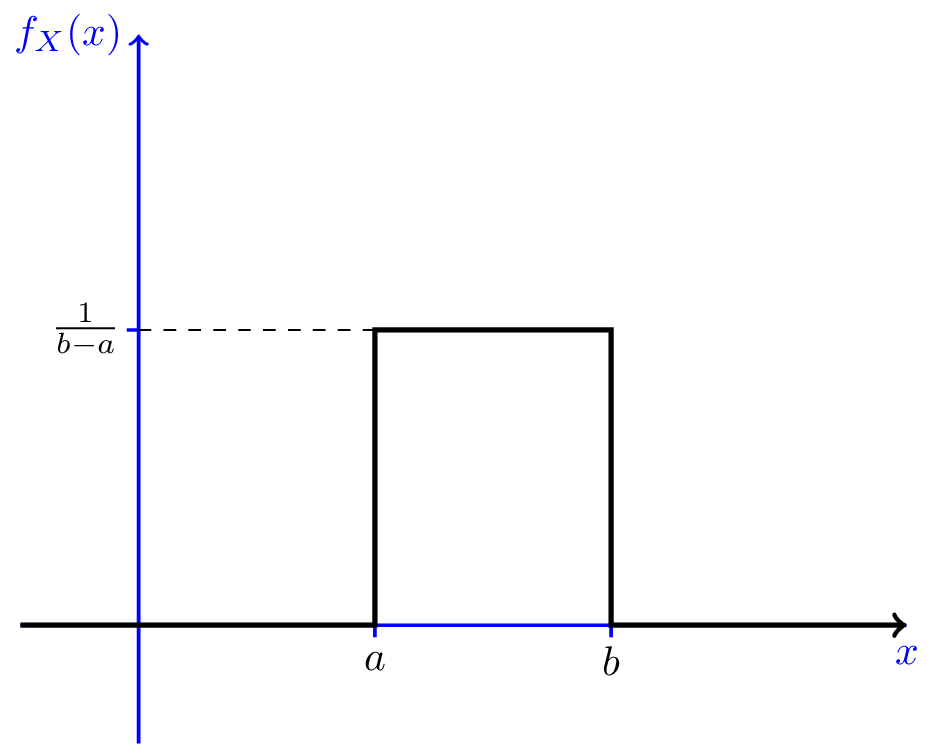
Esempio
Sia $ X $ una variabile casuale continua con il seguente PDF \ begin {equation} \ nonumber f_X (x) = \ left \ {\ begin {array} {ll} ce ^ {- x} & \ quad x \ geq 0 \\ 0 & \ quad \ text {altrimenti} \ end {array} \ right. \ end {equation} dove $ c $ è una costante positiva.

1. Trova $ c $.
2. Trova il CDF di X, $ F_X (x) $.
3. Trova $ P (1

Gamma