La pendenza di una collina è chiamata pendenza. Lo stesso vale per la pendenza di una linea. La pendenza è definita come il rapporto tra la variazione verticale tra due punti, la salita, e la variazione orizzontale tra gli stessi due punti, la corsa.

$$ pendenza = \ frac {rise} {corsa} = \ frac {modifica \: in \: y} {modifica \: in \: x} $$

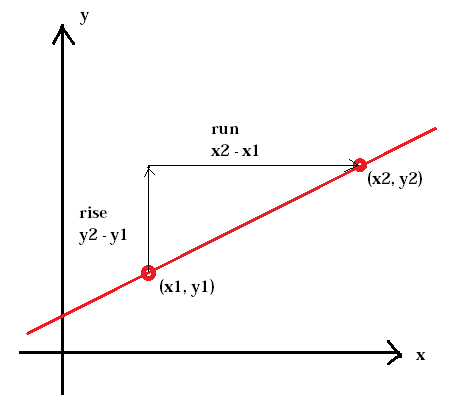
Il la pendenza di una linea è solitamente rappresentata dalla lettera m. (x1, y1) rappresenta il primo punto mentre (x2, y2) rappresenta il secondo punto.

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2 } \, -x_ {1}} $$

È importante mantenere le coordinate xey nello stesso ordine sia nel numeratore che nel denominatore altrimenti si otterrà una pendenza sbagliata.

Esempio

Trova la pendenza della linea

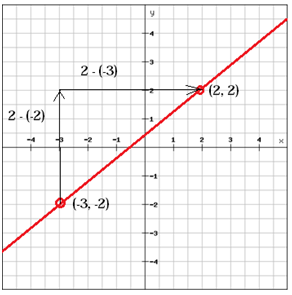
(x1, y1 ) = (-3, -2) e (x2, y2) = (2, 2)

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ { 2} \, -x_ {1}} = \ frac {2- \ left (-2 \ right)} {2- \ left (-3 \ right)} = \ frac {2 + 2} {2 + 3} = \ frac {4} {5} $$

Una linea con una pendenza positiva (m > 0), poiché la linea sopra, sale da sinistra a destra mentre una linea con una pendenza negativa (m < 0) cade da sinistra a destra.

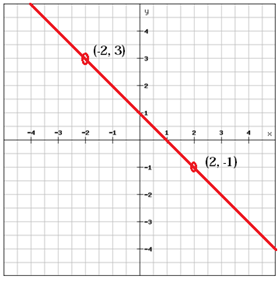
$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2} \, -x_ {1}} = \ frac {\ left (-1 \ right) -3} {2- \ left (-2 \ right)} = \ frac {-1-3} {2 + 2} = \ frac {-4} {4} = – 1 $$

Se due linee hanno la stessa pendenza, si dice che sono p arallel.

È possibile esprimere una funzione lineare utilizzando la forma di intercetta della pendenza.

$$ y = mx + b $$

$$ m = pendenza $ $

$$ b = y – intercetta $$

Video lezione

Trova la pendenza