力の計算

力はプッシュまたはプルです。
オブジェクトへの力は通常バランスが取れています(バランスが崩れている場合、オブジェクトは加速します):
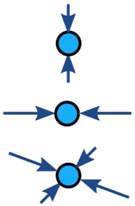 |
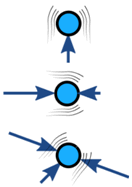 |
|
| バランスのとれた | アンバランスの | |
|---|---|---|
| 加速なし | 加速 |
例:このブリッジタワーの上部の力はバランスが取れています(加速していません):

ケーブルは左右に均等に下向きに引っ張られ、それはタワーの上向きのプッシュによってバランスが取られます(タワーはプッシュしますか?はい!タワーの代わりにそこに立っていると想像してください)。
次のように力をモデル化できます:

そしてそれらを真っ向から並べると、それらが互いに接近していることがわかります。つまり、正味の効果はゼロです。

力のバランスが取れています。
バランスの取れた力は平衡状態にあると言われています。動きにも変化はありません。
自由体図
最初のステップは自由体図(力図とも呼ばれます)を描画するには
自由体図:体に作用する力を除いて、体が世界から切り離されたスケッチ。
橋の例では、塔の上部の自由体図は次のとおりです。

自由体図
体に作用する力について明確に考える必要があります。
例:高速道路の車
高速道路をクルージングする車の力は何ですか?

エンジンが一生懸命働いているのに、なぜ車は加速し続けないのですか?
運転しているからです力のバランスは次のとおりです。
- 空気抵抗(簡単に言えば:th e空気は押しのけられない)、
- 転がり抵抗。転がり摩擦とも呼ばれます(タイヤの形状が変化するのを防ぎます)

自由体図
Wは車の重量、
R1とR2はタイヤの転がり抵抗
N1とN2は反力です(車の重量のバランスを取ります)。
注:スチールホイール(電車のように)は転がり抵抗が少ないですが、路上では滑りすぎます!
計算
力はベクトルです。ベクトルには大きさ(サイズ)と方向があります:

正しいサイズと方向の矢印を描くことで、力をモデル化できます。このように:
例:景色を眺める
ブレイディは、水平の梁と支柱で支えられたバルコニーの端に立っています:

体重80kg。
力は何ですか?
彼が立っている場所を見て、そこにある力について考えてみましょう。

彼の体重
彼の80kgの質量は、重力によって下向きの力を生み出します。
力は質量と加速度の積です:F = ma
地球上の重力による加速度は9.81m / s2です。 、したがって、a = 9.81 m / s2
F = 80kg×9.81m / s2
F = 785 N
その他の力
力はバランスが取れているので、次のように閉じます。

三角測量を使用してそれを解決できます。
直角の三角形なので、SOHCAHTOAが役立ちます。
ビームの場合、隣接するものを知り、反対側を知りたいので、「TOA」はタンジェントを使用するように指示します。
tan(60° )=ビーム/ 785N
ビーム/ 785N = tan(60°)
ビーム= tan(60°)×785 N
ビーム= 1.732 …×785N = 1360 N
Strutの場合、隣接を知っており、Hypotenuseを知りたいので、「CAH」はコサインを使用するように指示します。
cos (60°)= 785 N /ストラット
ストラット×cos(60°)= 785 N
ストラット= 785 N / cos(60°)
Strut = 785 N / 0.5 = 1570 N
解決済み:

どのくらいの力がかかっているか興味深い支えられている重量と比較した梁と支柱!
トルク(またはモーメント)
梁が壁(カンチレバーと呼ばれる)に突き刺さった場合はどうなりますか?

支柱がないので、力はどうなりますか?
フリーボディダイアグラム次のようになります。

上向きの力Rは下向きの重量のバランスを取ります。
この2つだけでビームがプロペラのように回転するように強制します!しかし、モーメント(またはトルク)と呼ばれる「回転効果」Mもあり、バランスを取ります。
モーメント:力に直角の距離を掛けたものです。
重量は次のとおりです。 785 Nであり、直角の距離も知る必要があります。この場合は3.2mです。
M = 785 N x 3.2 m = 2512 Nm
そしてそのモーメントビームの回転を止めるものです。

釣り棒を握ると瞬間を感じることができます。
重量を維持するだけでなく、下向きに回転しないようにする必要があります。
摩擦
ランプ上のボックス
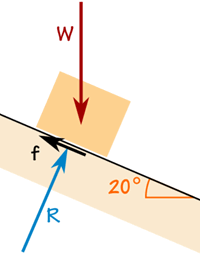
箱の重さは100kgです。
摩擦力は箱を所定の位置に保つのに十分です。
反力Rはランプ。
ボックスが加速していないため、力のバランスが取れています。
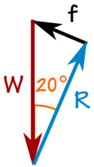
100 kgの質量は、摩擦により下向きの力を生み出します。
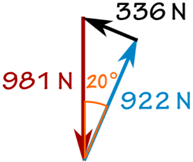
W = 100kg×9.81m / s2 = 981 N
SOHCAHTOAを使用して三角形を解くことができます。
摩擦f:
sin(20°)= f / 981 N
f = sin(20°)×981 N = 336 N
反作用N:
cos(20°)= R / 981 N
R = cos(20°)×981 N = 922 N
そして、次のようになります。
自由体図を描画するためのヒント
- できるだけ簡単に描画します。多くの場合、ボックスで十分です。
- 力は体に作用する方向を指します
- 力の直線矢印
- 瞬間の曲線矢印
SamとAlexがボックスを引っ張る
大きさと方向をxとyに変換すると、計算が簡単になる場合があります。
 |
< = > |  |
| 極座標のベクトルa 座標 |
デカルト座標でのベクトルa 座標 |
極座標とデカルト座標で変換する方法を読むことができます調整しますが、ここに簡単な要約があります:
それらを使用しましょう!