統計：パラメトリック検定とノンパラメトリック検定

このセクションカバー：

• テストの選択
• パラメトリック検定
• ノンパラメトリック検定

テストの選択

統計的検定の選択に関して、最も重要な質問は「主な研究仮説は何ですか？」です。場合によっては、仮説がありません。捜査官はただ「そこにあるものを見たい」だけです。たとえば、有病率調査では、テストする仮説はなく、調査の規模は、調査員が有病率をどれだけ正確に決定したいかによって決まります。仮説がない場合、統計的検定はありません。どの仮説が確認的であるか（つまり、いくつかの前提となる関係をテストしている）、どの仮説が探索的であるか（データによって示唆されている）を事前に決定することが重要です。単一の研究で一連の仮説全体をサポートすることはできません。賢明な計画は、確認仮説の数を厳しく制限することです。データによって示唆された仮説に対して統計的検定を使用することは有効ですが、P値はガイドラインとしてのみ使用する必要があり、結果は後続の研究で確認されるまで暫定的なものとして扱われます。有用なガイドは、ボンフェローニ補正を使用することです。これは、n個の独立した仮説をテストする場合、0.05 / nの有意水準を使用する必要があることを簡単に示しています。したがって、2つの独立した仮説があった場合、結果はP < 0.025の場合にのみ有意であると宣言されます。テストが独立していることはめったにないため、これは非常に保守的な手順です。つまり、帰無仮説を棄却する可能性は低いことに注意してください。次に、調査員は「データは独立していますか？」と尋ねる必要があります。これを決定するのは難しい場合がありますが、経験則として、同じ個人または一致した個人からの結果は独立していません。したがって、クロスオーバー試験の結果、または対照が年齢、性別、社会階級によって症例と一致した症例対照研究の結果は独立していません。

• 分析は設計を反映する必要があります、したがって、一致した設計の後に一致した分析を行う必要があります。
• 時間の経過とともに測定された結果には、特別な注意が必要です。統計分析で最もよくある間違いの1つは、相関変数を
  独立しているかのように扱うことです。たとえば、下腿潰瘍の治療を検討していたとします。下腿潰瘍では、各脚に潰瘍がある人がいます。潰瘍が30人の被験者が20人いる可能性がありますが、1人の各脚の潰瘍の状態は、その人の健康状態とその分析によって影響を受ける可能性があるため、独立した情報の数は20です。独立した観察として潰瘍を考慮したのは正しくないでしょう。ペアのデータとペアのないデータの混合を正しく分析するには、統計学者に相談してください。

次の質問は、「どのタイプのデータが測定されているか」です。使用するテストは、データによって決定する必要があります。一致またはペアのデータの検定の選択を表1に、独立したデータのテストの選択を表2に示します。

表1ペアまたは一致の観測からの統計的検定の選択

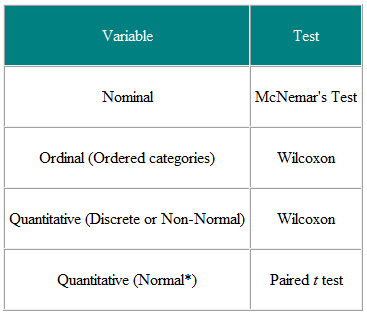
入力変数と結果変数を決定すると便利です。たとえば、臨床試験では、入力変数は治療のタイプ（名目変数）であり、結果はおそらく正規分布の何らかの臨床測定値である可能性があります。その場合、必要なテストはt検定です（表2）。ただし、入力変数が連続的である場合、たとえば臨床スコアであり、結果が名目上、たとえば治癒したか治癒していない場合は、ロジスティック回帰が必要な分析です。この場合のt検定は役立つかもしれませんが、必要なもの、つまり臨床スコアの特定の値に対する治癒の確率は得られません。別の例として、一般開業医が良い仕事をしていると思うかどうかを5段階でランダムにサンプルに尋ねる横断研究があり、女性の意見が高いかどうかを確認したいとします。男性よりも一般開業医の。入力変数は、名目上の性別です。結果変数は、5ポイントの順序尺度です。各人の意見は他の人から独立しているため、独立したデータがあります。表2から、傾向のχ2検定、または同点の補正を伴うマンホイットニーU検定を使用する必要があります（NB同点は2つ以上で発生します値は同じであるため、ランクの厳密な昇順はありません。これが発生した場合、同値のランクを平均できます）。ただし、一般開業医を共有する人と共有しない人がいる場合、データはそうではありません。独立した、より洗練された分析が求められます。これらの表はガイドとしてのみ考慮されるべきであり、それぞれのケースはそのメリットについて考慮されるべきであることに注意してください。

表2独立した観測値の統計的検定の選択

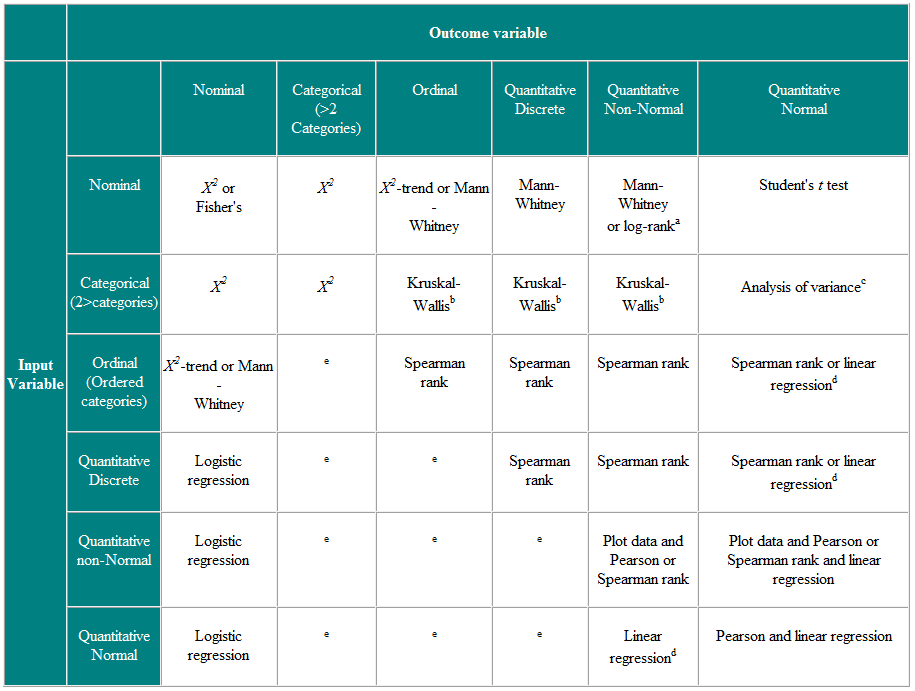
aデータが打ち切られている場合。 b Kruskal-Wallis検定は、3つ以上のグループの順序変数または非正規変数を比較するために使用され、Mann-WhitneyU検定を一般化したものです。 c分散分析は一般的な手法であり、1つのバージョン（一元配置分散分析）を使用して、3つ以上のグループの正規分布変数を比較します。これは、クラスカル・ウォリス検定と同等のパラメトリックです。 d結果変数が従属変数である場合、残差（観測値と回帰からの予測応答の差）がもっともらしく正規分布している場合、独立変数の分布は重要ではありません。 eこれらの状況に対処するために、ポアソン回帰などのより高度な手法がいくつかあります。ただし、特定の仮定が必要であり、結果変数を二分するか、連続として扱う方が簡単な場合がよくあります。

パラメトリック検定は、サンプルが抽出される母集団分布のパラメーターについて仮定を行うものです。 。これは、母集団データが正規分布しているという仮定であることがよくあります。ノンパラメトリック検定は「分布なし」であるため、非正規変数に使用できます。表3は、いくつかのパラメトリック検定に相当するノンパラメトリックを示しています。

表3パラメトリック検定と2つ以上のグループを比較するためのノンパラメトリック検定

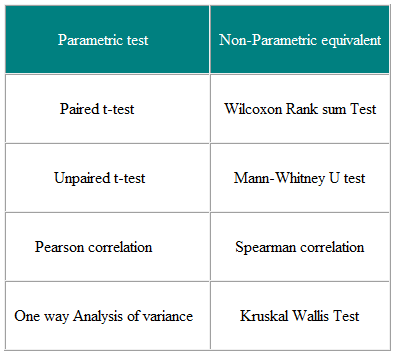
ノンパラメトリック検定は、非正規分布データと非正規分布データの両方に有効です。正規分布のデータなので、常に使用しないのはなぜですか？

すべての場合にノンパラメトリック検定を使用するのが賢明であるように思われます。これにより、正規性の検定の手間が省けます。パラメトリック検定をお勧めします。ただし、次の理由によります。

1.有意性検定だけに関心があることはめったにありません。サンプルの出所である母集団について何か言いたいのですが、これは
で行うのが最適です。パラメータと信頼区間の推定。

2。たとえば、複数を使用して交絡因子を考慮に入れるなど、ノンパラメトリック検定で柔軟なモデリングを行うことは困難です。回帰。

3。パラメトリック検定は通常、ノンパラメトリック検定よりも統計的検出力があります。言い換えると、
実際に存在する場合に有意差を検出する可能性が高くなります。

ノンパラメトリック検定は中央値を比較しますか？

一般的に考えられているのは、 Mann-Whitney U検定は、実際には中央値の違いの検定です。ただし、2つのグループの中央値が同じでありながら、有意なマンホイットニーU検定を行う可能性があります。それぞれが100個の観測値を持つ2つのグループの次のデータを検討してください。グループ1：98（0）、1、2;グループ2：51（0）、1、48（2）。どちらの場合も中央値は0ですが、マンホイットニー検定からP < 0.0001です。 2つのグループの違いが単に場所のシフトである（つまり、一方のグループのデータの分布が他方から一定量だけシフトする）という追加の仮定を立てる準備ができている場合にのみ、次のように言えます。テストは、中央値の差のテストです。ただし、グループの分布が同じである場合、場所を移動すると中央値と平均値が同じ量だけ移動するため、中央値の差は平均値の差と同じになります。したがって、マンホイットニーのU検定は、平均の差の検定でもあります。マンホイットニーのU検定はt検定とどのように関連していますか？データ自体ではなくデータのランクを2つのサンプルのt検定プログラムに入力した場合、得られるP値はマンホイットニーのU検定によって生成された値に非常に近くなります。