離散確率変数の分布を決定するために、PMFまたはCDFのいずれかを提供できます。連続確率変数の場合、CDFは明確に定義されているため、CDFを提供できます。ただし、PMFは、すべての$ x \ in \ mathbb {R} $に対して連続確率変数$ P（X = x）= 0 $であるため、連続確率変数では機能しません。代わりに、通常、確率密度関数（PDF）を定義できます。 PDFは、確率質量ではなく確率密度です。概念は物理学の質量密度と非常に似ています。その単位は単位長さあたりの確率です。 PDFの感覚をつかむには、連続確率変数$ X $を検討し、関数$ f_X（x）$を次のように定義します（制限が存在する場合）：$$ f_X（x）= \ lim _ {\ Delta \ rightarrow 0 ^ +} \ frac {P（x

$$ f_X（x）= \ lim _ {\ Delta \ rightarrow 0} \ frac {F_X（x + \ Delta） -F_X（x）} {\ Delta} $$ $$ = \ frac {dF_X（x）} {dx} = F ” _X（x）、\ hspace {20pt} \ textrm {if} F_X（x）\ textrm {は} x。$$

で微分可能です。したがって、次の定義があります。連続確率変数のPDF：

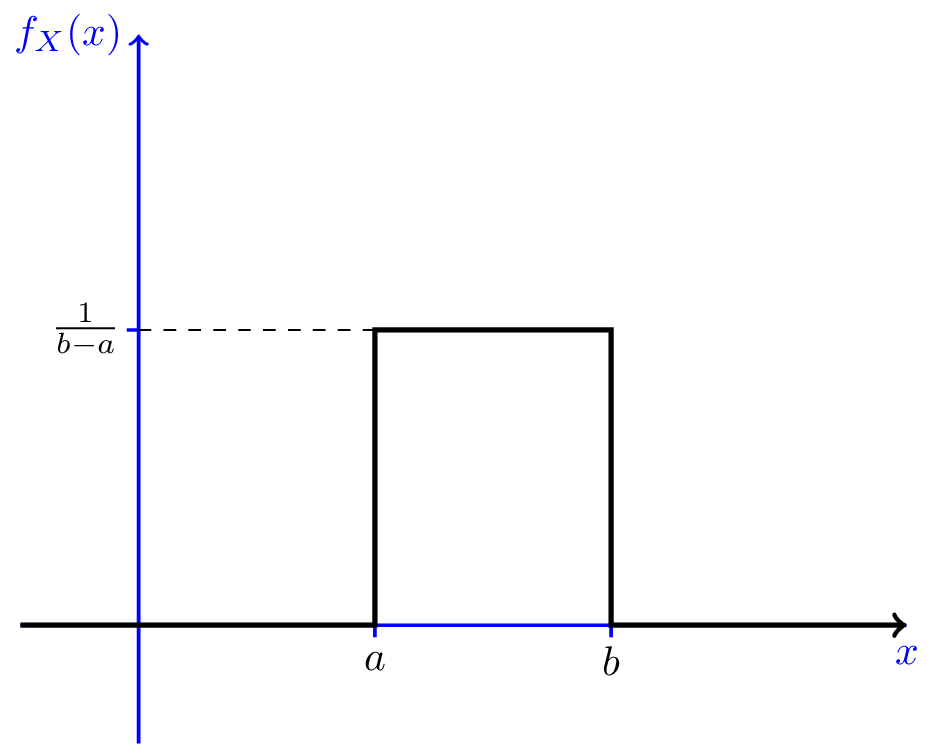
例
$ X $を、次のPDF \ begin {equation} \ nonumber f_X（x）=の連続確率変数とします。 \ left \ {\ begin {array} {ll} ce ^ {-x} & \ quad x \ geq 0 \\ 0 & \ quad \ text {otherwise} \ end {array} \ right。\ end {equation}ここで、$ c $は正の定数。

1. $ c $を検索します。
2. XのCDF、$ F_X（x）$を検索します。
3. $ P（1

範囲