機械学習のためのK最近傍(KNN)アルゴリズム
- K最近傍は、ベースの最も単純な機械学習アルゴリズムの1つです。監視学習手法について。
- K-NNアルゴリズムは、新しいケース/データと利用可能なケースの類似性を想定し、新しいケースを利用可能なカテゴリに最も類似したカテゴリに分類します。
- K-NNアルゴリズムは、利用可能なすべてのデータを保存し、類似性に基づいて新しいデータポイントを分類します。これは、新しいデータが表示されたときに、K-NNアルゴリズムを使用してウェルスイートカテゴリに簡単に分類できることを意味します。
- K-NNアルゴリズムは、分類だけでなく回帰にも使用できますが、ほとんどの場合、分類問題に使用されます。
- K-NNは非パラメトリックアルゴリズムです。つまり、基礎となるデータを想定していません。
- トレーニングセットからすぐに学習せず、代わりにデータセットを保存し、分類時に実行するため、レイジーラーナーアルゴリズムとも呼ばれます。データセットに対するアクション。
- トレーニングフェーズのKNNアルゴリズムは、データセットを保存するだけで、新しいデータを取得すると、そのデータを新しいデータと非常によく似たカテゴリに分類します。
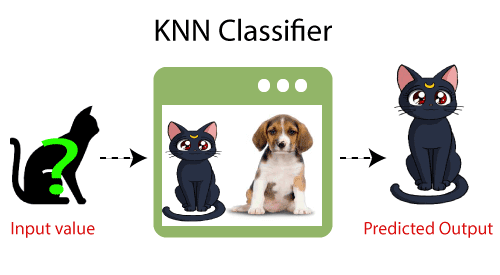
- 例:猫と犬に似た生き物の画像がありますが、それが猫か犬かを知りたいとします。したがって、この識別には、類似性の尺度で機能するKNNアルゴリズムを使用できます。 KNNモデルは、猫と犬の画像に新しいデータセットの類似した機能を見つけ、最も類似した機能に基づいて、猫または犬のカテゴリに分類します。
K-NNアルゴリズムが必要な理由
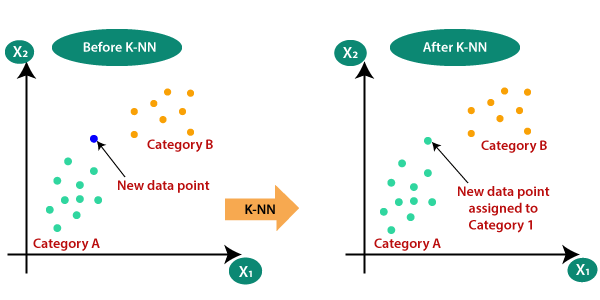
カテゴリAとカテゴリBの2つのカテゴリがあり、新しいデータポイントx1があるとします。したがって、このデータポイントは、これらのカテゴリのどれにあります。このタイプの問題を解決するには、K-NNアルゴリズムが必要です。 K-NNの助けを借りて、特定のデータセットのカテゴリまたはクラスを簡単に識別できます。次の図を検討してください。
K-NNはどのように機能しますか?
K-NNの機能は以下に基づいて説明できます。以下のアルゴリズム:
- ステップ-1:近傍の数Kを選択します
- ステップ-2:近傍のK個のユークリッド距離を計算します
- ステップ3:計算されたユークリッド距離に従ってK最近傍を取得します。
- ステップ4:これらのk近傍のうち、各カテゴリのデータポイントの数を数えます。
- ステップ-5:近傍の数が最大であるカテゴリに新しいデータポイントを割り当てます。
- ステップ-6:モデルの準備ができています。
新しいデータポイントがあり、それを必要なカテゴリに入れる必要があるとします。次の画像について考えてみます。
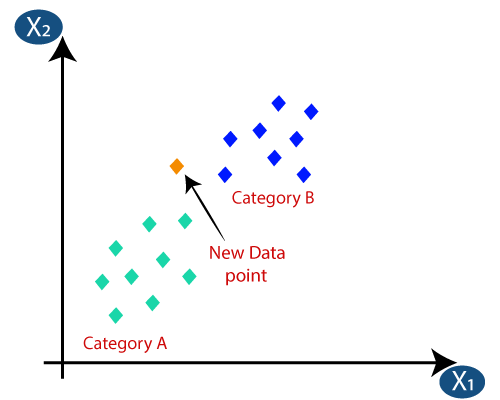
- まず、ネイバーの数を選択するので、k = 5を選択します。
- 次に、データポイント間のユークリッド距離を計算します。ユークリッド距離は、幾何学ですでに研究した2点間の距離です。これは次のように計算できます。
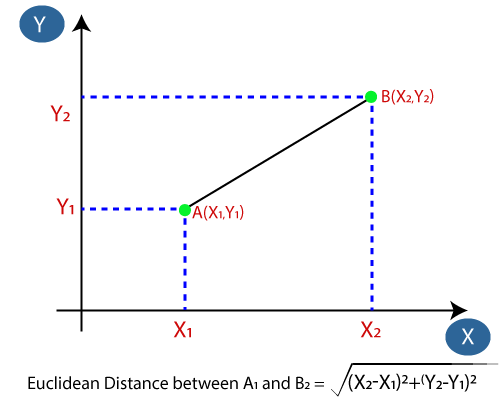
- ユークリッド距離を計算することにより、カテゴリAの3つの最近傍として最近傍を取得しました。次の画像を検討してください。
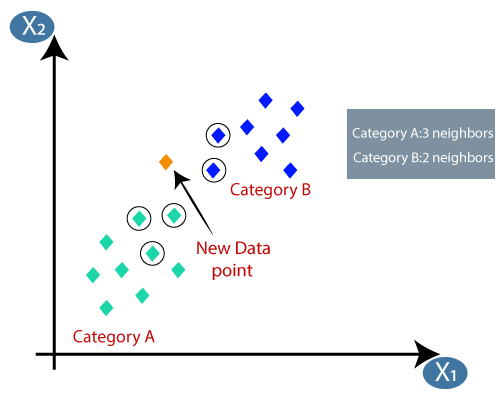
- ご覧のとおり、3つの最近傍はカテゴリからのものです。 A、したがって、この新しいデータポイントはカテゴリAに属している必要があります。
K-NNアルゴリズムでKの値を選択する方法は?
以下にいくつかのポイントを示します。 K-NNアルゴリズムでKの値を選択するときは、次の点に注意してください。
- 「K」の最適な値を決定する特別な方法はないため、最適な値を見つけるためにいくつかの値を試す必要があります。それらのうち。 Kの最も好ましい値は5です。
- K = 1やK = 2などのKの非常に低い値は、ノイズが多く、モデルの外れ値の影響をもたらす可能性があります。
- Kの値は大きいのが適切ですが、問題が発生する可能性があります。
KNNアルゴリズムの利点:
- 実装は簡単です。
- ノイズの多いトレーニングデータに対して堅牢です
- トレーニングデータが大きい場合はより効果的です。
KNNアルゴリズムの欠点:
- いつか複雑になる可能性のあるKの値を常に決定する必要があります。
- すべてのトレーニングサンプルのデータポイント間の距離を計算するため、計算コストが高くなります。 。
KNNアルゴリズムのPython実装
K-NNアルゴリズムのPython実装を行うために、で使用したのと同じ問題とデータセットを使用します。ロジスティック回帰。ただし、ここではモデルのパフォーマンスを向上させます。問題の説明は次のとおりです。
K-NNアルゴリズムの問題:新しいSUV車を製造している自動車メーカーの会社があります。同社は、そのSUVの購入に関心のあるユーザーに広告を提供したいと考えています。したがって、この問題では、ソーシャルネットワークを介した複数のユーザーの情報を含むデータセットがあります。データセットには多くの情報が含まれていますが、独立変数については推定給与と年齢を考慮し、従属変数については購入変数を考慮します。データセットは次のとおりです。
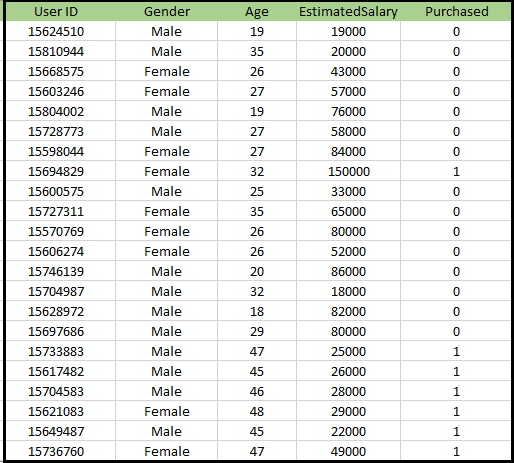
K-NNアルゴリズムを実装する手順:
- データの前処理手順
- K-NNアルゴリズムをトレーニングセットに適合させる
- テスト結果を予測する
- 結果のテスト精度(混同行列の作成)
- テストセットの結果を視覚化する。
データの前処理ステップ:
データの前処理ステップは、ロジスティック回帰とまったく同じままです。以下はコードです。そのため:
上記のコードを実行すると、データセットがプログラムにインポートされ、適切に前処理されます。機能のスケーリング後、テストデータセットは次のようになります。
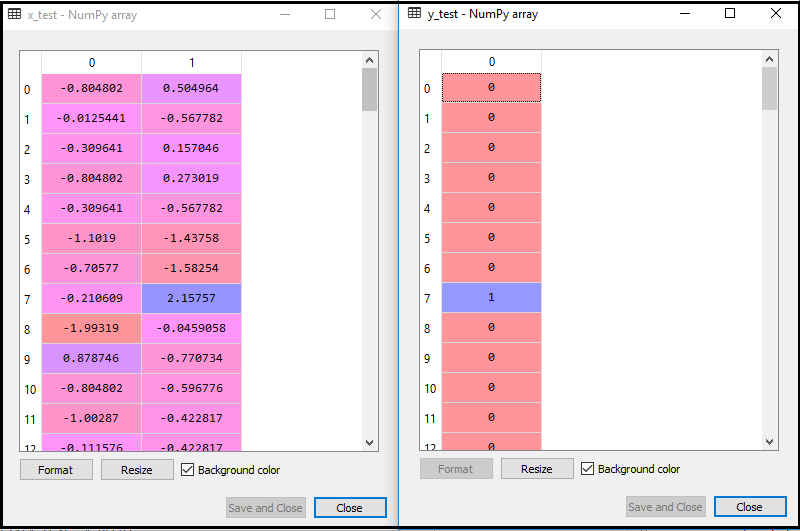
上記の出力からim年齢を重ねると、データが正常にスケーリングされていることがわかります。
- K-NN分類器をトレーニングデータに適合させる:
次に、K-NN分類器をトレーニングデータに適合させます。これを行うには、SklearnNeighborsライブラリのKNeighborsClassifierクラスをインポートします。クラスをインポートした後、クラスのClassifierオブジェクトを作成します。このクラスのパラメータは次のようになります。- n_neighbors:アルゴリズムの必要なネイバーを定義します。通常、5がかかります。
- metric = “minkowski”:これはデフォルトのパラメータであり、ポイント間の距離を決定します。
- p = 2:標準と同等です。ユークリッド距離。
次に、分類器をトレーニングデータに適合させます。そのためのコードは次のとおりです。
出力:上記のコードを実行すると、次のような出力が得られます。
- テスト結果の予測:テストセットの結果を予測するために、ロジスティック回帰で行ったようにy_predベクトルを作成します。そのためのコードは次のとおりです。
出力:
上記のコードの出力は次のようになります。
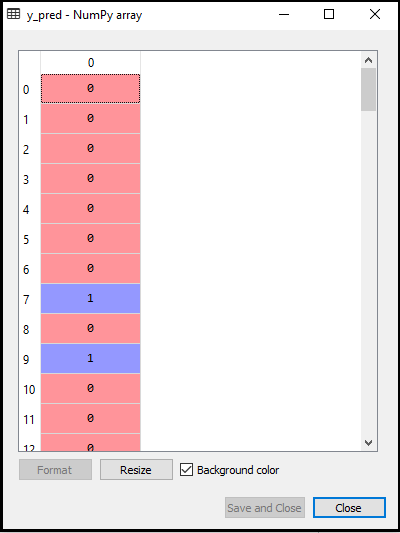
- 混同行列の作成:
次に、K-NNモデルの混同行列を作成して、分類器の精度を確認します。そのためのコードは次のとおりです。
上記のコードでは、confusion_matrix関数をインポートし、変数cmを使用して呼び出しています。
出力:上記のコードを実行すると、次のような行列が得られます。
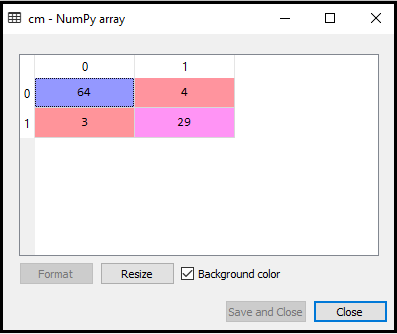
上の画像では、次のように表示されます。 64 + 29 = 93の正しい予測と3+ 4 = 7の誤った予測がありますが、ロジスティック回帰では11の誤った予測がありました。したがって、K-NNアルゴリズムを使用することで、モデルのパフォーマンスが向上したと言えます。
- トレーニングセットの結果の視覚化:
次に、Kのトレーニングセットの結果を視覚化します。 -NNモデル。コードは、グラフの名前を除いて、ロジスティック回帰で行ったものと同じままです。そのためのコードは次のとおりです。
出力:
上記のコードを実行すると、次のグラフが表示されます。
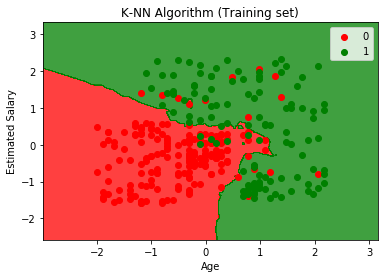
出力グラフは、ロジスティック回帰で発生したグラフとは異なります。以下の点で理解できます。
- ご覧のとおり、グラフは赤い点と緑の点を示しています。緑のポイントはPurchased(1)変数用で、赤のポイントはPurchased(0)変数ではありません。
- グラフは、K-NNアルゴリズムであるため、つまり最近傍を見つけるため、直線や曲線ではなく、不規則な境界を示しています。
- SUVを購入しなかったユーザーのほとんどが赤の領域にあり、SUVを購入したユーザーが緑の領域にあるため、グラフはユーザーを正しいカテゴリに分類しています。
- グラフは良好な結果を示していますが、それでも、赤の領域にいくつかの緑の点と緑の領域に赤の点があります。ただし、このモデルを実行することで過剰適合の問題が防止されるため、これは大きな問題ではありません。
- したがって、モデルは十分にトレーニングされています。
- テストセットの結果の視覚化:
モデルのトレーニング後、新しいデータセットを配置して結果をテストします。テストデータセット。コードは、x_trainやy_trainがx_testやy_testに置き換えられるなど、いくつかの小さな変更を除いて同じままです。
以下はそのコードです:
出力:
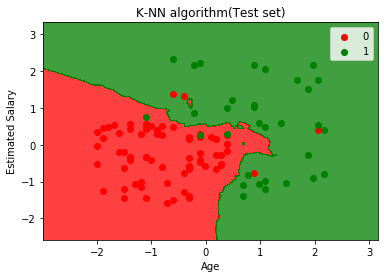
上のグラフは、テストデータセットの出力を示しています。グラフからわかるように、予測された出力は良好です。ほとんどの赤い点が赤い領域にあり、ほとんどの緑の点は緑の領域にあります。
ただし、赤の領域には緑の点がほとんどなく、緑の領域には赤の点がいくつかあります。したがって、これらは混同行列で観察された誤った観測です(7誤った出力)。