遺伝子型
遺伝子型
n。、ˈdʒiːn.oʊ.taɪp
細胞、生物、またはその形質や表現型に寄与する個人
目次
レビュー担当者:Mary Anne Clark、PhD
遺伝子型と表現型
対照的な用語である遺伝子型と表現型は、生物の特徴や特徴を定義します。遺伝子型は、単一の形質(Aaなど)または複数の形質(Aa Bb ccなど)に関連する対立遺伝子を識別します。この用語は、生物(または分類群)の遺伝子のセット全体を指すように拡張できます。この包括的なレベルでは、生物内のすべてのDNAを指すゲノムという用語と多少重複しています。ただし、すべてのDNAが遺伝子で構成されているわけではありません。生物の遺伝子型を完全に書き出すには、ヒトゲノム内の約20,000個の既知の遺伝子のそれぞれの対立遺伝子を表す文字のセットが必要です。
表現型は、生物の物理的または生理学的特徴を表し、遺伝子型の発現の結果です。ただし、個人の表現型を決定する要因は遺伝子型だけではありません。さまざまな環境要因も役割を果たしており、これらは遺伝子の発現に影響を与えて、生物の特徴的な表現型を決定します。
遺伝子、遺伝子型、対立遺伝子
ほとんどの真核生物では、遺伝子は対立遺伝子と呼ばれるペアで提供されます。対になった対立遺伝子は、染色体上の同じ場所(遺伝子座と呼ばれます)を占めます。彼らはまた、同じ特性を制御します。対立遺伝子という用語は、特定の遺伝子の変異体を指します。ほとんどの真核生物は有性生殖を行うため、各親は特定の遺伝子の2つの対立遺伝子のうちの1つに寄与します。各親は異なる系統の生物の産物であるため、ランダムな複製エラーとDNAとの環境相互作用により、各親の遺伝子に異なる変更が加えられました。この違いは、他者性または違いを意味する「対立遺伝子」(allo = other)という用語の基礎です。
形質が単純なメンデルの法則の遺伝形式に従っている場合、対立遺伝子の1つが表現されます。発現している対立遺伝子は優性対立遺伝子であると言われていますが、そうでない対立遺伝子は劣性と呼ばれています。優性対立遺伝子が存在しない場合、劣性対立遺伝子の発現が起こります。
優性対立遺伝子が「A」とラベル付けされ、劣性対立遺伝子が「a」とラベル付けされている場合、「AA」、「aa」、および「Aa」の3つの異なる遺伝子型が可能です。 「ホモ接合」という用語は、「AA」と「aa」のペアを説明するために使用されます。これは、ペアの対立遺伝子が同じ、つまり両方が優性または両方が劣性であるためです。対照的に、「ヘテロ接合」という用語は、対立遺伝子ペアを説明するために使用されます。 、「Aa」。優性形質は遺伝子型AAまたはAaの個体の表現型で発現し、劣性表現型は遺伝子型aaの個体で発現します。すべての形質が単一の遺伝子によって決定されるわけではなく、多くの遺伝子が複数の対立遺伝子を持っています変異体であり、すべての遺伝子ペアが単純な優性/劣性関係にあるわけではありません。共優性、不完全優性、および多遺伝子型遺伝は、非メンデリア型の遺伝の例です。ヒトでは、観察可能な形質の多くは非メンデリアです。身長と皮膚の色たとえば、対立遺伝子のペアだけでなく、いくつかの異なる遺伝子座にある遺伝子の相互作用によってもたらされます。
単純な遺伝子型の予測:パネットスクエア
単純な遺伝子型では、 1つまたはafのみの対立遺伝子いくつかの特性が指定されています。たとえば、エンドウ豆の花の色を決定する遺伝子の遺伝子型は、2つの対立遺伝子Bとbで表されます。 Bは優性対立遺伝子であり、「b」は劣性対立遺伝子です。優性対立遺伝子は紫色の花の形質をコードし、劣性対立遺伝子は白い花の形質をコードします。下のグラフの図を参照してください。
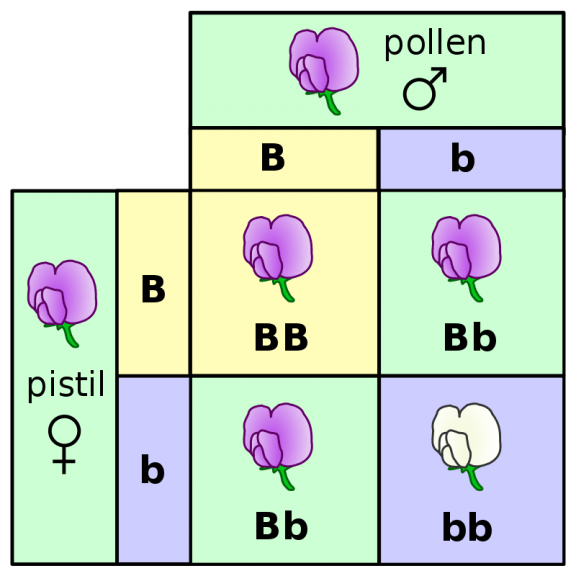
この図は、メンデルの研究の再発見後にReginald Punnettによって最初に導入されたPunnett正方形の例です。Punnett正方形は、遺伝を予測するための遺伝学において不可欠なツールです。パターンと比率。この正方形は、2つのヘテロ接合(Bb)の親の子孫の遺伝子型と表現型の両方を示しており、両方とも紫色の花を持っています。図では、親の配偶子とそれらのさまざまな組み合わせによって生成された子孫に存在する対立遺伝子配偶子が表されます。各親は2種類の配偶子(Bとb)を生成し、それらはすべての可能なペアで組み合わされます.4つの子孫のうち、2つはホモ接合、1つは紫(BB)、1つは白(bb)、2つはヘテロ接合です(Bb)、両方とも優性形質を紫色で表現している。これにより、メンデルによって記述された優性:劣性表現型の3:1の表現型比が得られます。 また、BB、Bb、およびbbの遺伝子型の1:2:1の遺伝子型比も得られます。
関連項目
- 対立遺伝子
- 遺伝子
- ゲノム
- メンデルの法則