• K-Nearest Neighbor ist einer der einfachsten Algorithmen für maschinelles Lernen
• Der K-NN-Algorithmus nimmt die Ähnlichkeit zwischen dem neuen Fall / den neuen Daten und den verfügbaren Fällen an und ordnet den neuen Fall der Kategorie zu, die den verfügbaren Kategorien am ähnlichsten ist.

Der K-NN-Algorithmus speichert alle verfügbaren Daten und klassifiziert einen neuen Datenpunkt basierend auf der Ähnlichkeit. Das heißt, wenn neue Daten erscheinen, können sie mithilfe des K-NN-Algorithmus leicht in eine Well-Suite-Kategorie eingeteilt werden.

Der K-NN-Algorithmus kann sowohl für die Regression als auch für die Klassifizierung verwendet werden, wird jedoch meistens für die Klassifizierungsprobleme verwendet.

K-NN ist ein nicht parametrischer Algorithmus Es werden keine Annahmen zu den zugrunde liegenden Daten getroffen.

Es wird auch als Lazy-Learning-Algorithmus bezeichnet, da es nicht sofort aus dem Trainingssatz lernt, sondern den Datensatz speichert und zum Zeitpunkt der Klassifizierung eine ausführt Aktion für den Datensatz.

Der KNN-Algorithmus in der Trainingsphase speichert nur den Datensatz. Wenn neue Daten abgerufen werden, werden diese Daten in eine Kategorie eingeteilt, die den neuen Daten sehr ähnlich ist.

Beispiel: Angenommen, wir haben ein Bild einer Kreatur, die Katze und Hund ähnelt, aber wir möchten wissen, ob es sich um eine Katze oder einen Hund handelt. Für diese Identifizierung können wir den KNN-Algorithmus verwenden, da er mit einem Ähnlichkeitsmaß arbeitet. Unser KNN-Modell findet die ähnlichen Merkmale des neuen Datensatzes wie die Bilder von Katzen und Hunden und ordnet ihn basierend auf den ähnlichsten Merkmalen entweder der Kategorie Katzen oder Hunde zu.

Warum benötigen wir einen K-NN-Algorithmus?

Angenommen, es gibt zwei Kategorien, dh Kategorie A und Kategorie B, und wir haben einen neuen Datenpunkt x1. Dieser Datenpunkt liegt also in welcher dieser Kategorien. Um diese Art von Problem zu lösen, benötigen wir einen K-NN-Algorithmus. Mit Hilfe von K-NN können wir die Kategorie oder Klasse eines bestimmten Datensatzes leicht identifizieren. Betrachten Sie das folgende Diagramm:

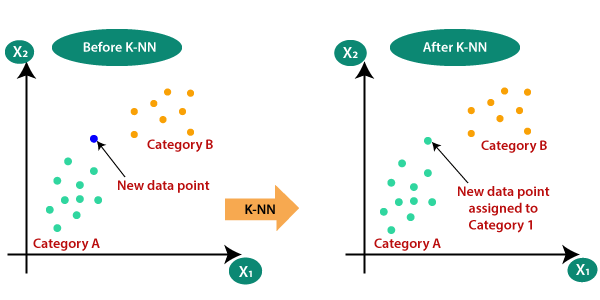
Wie funktioniert K-NN?

Die K-NN-Funktionsweise kann anhand von erklärt werden Der folgende Algorithmus:

• Schritt 1: Wählen Sie die Anzahl K der Nachbarn aus.
• Schritt 2: Berechnen Sie den euklidischen Abstand von K Anzahl der Nachbarn

chritt 3: Nehmen Sie die K nächsten Nachbarn gemäß der berechneten euklidischen Entfernung.

• Schritt 4: Zählen Sie unter diesen k Nachbarn die Anzahl der Datenpunkte in jeder Kategorie.
• Schritt 5: Weisen Sie die neuen Datenpunkte der Kategorie zu, für die die Anzahl der Nachbarn maximal ist.
• Schritt 6: Unser Modell ist bereit.

Angenommen, wir haben einen neuen Datenpunkt und müssen ihn in die erforderliche Kategorie einordnen. Betrachten Sie das folgende Bild:

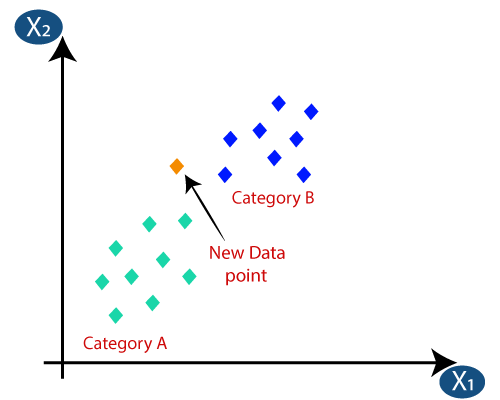
• Zuerst wählen wir die Anzahl der Nachbarn, also wählen wir k = 5.
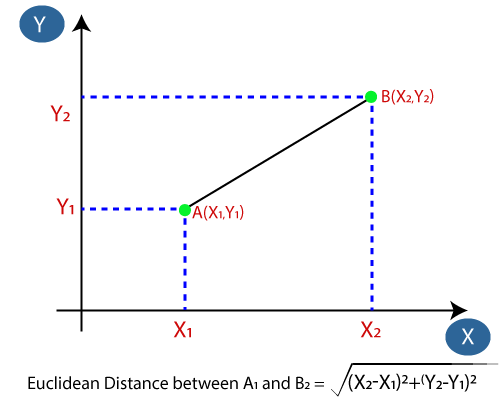
• Als nächstes berechnen wir den euklidischen Abstand zwischen den Datenpunkten. Der euklidische Abstand ist der Abstand zwischen zwei Punkten, den wir bereits in der Geometrie untersucht haben. Es kann berechnet werden als:

• Durch Berechnung der euklidischen Entfernung erhielten wir die nächsten Nachbarn als drei nächste Nachbarn in Kategorie A. und zwei nächste Nachbarn in Kategorie B. Betrachten Sie das folgende Bild:

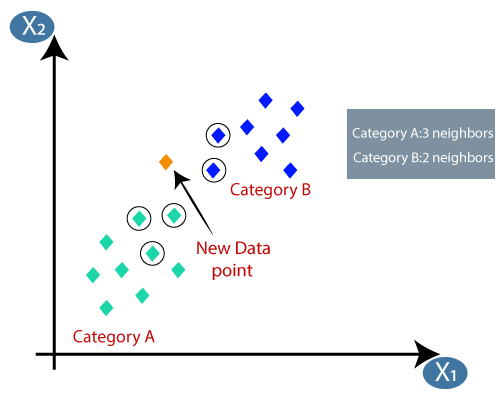
• Wie wir sehen können, stammen die 3 nächsten Nachbarn aus der Kategorie A, daher muss dieser neue Datenpunkt zur Kategorie A gehören.

Wie wählt man den Wert von K im K-NN-Algorithmus aus?

Nachfolgend sind einige Punkte aufgeführt Denken Sie bei der Auswahl des Werts von K im K-NN-Algorithmus daran:

• Es gibt keine bestimmte Möglichkeit, den besten Wert für „K“ zu ermitteln. Daher müssen wir einige Werte ausprobieren, um den besten zu finden aus ihnen heraus. Der am meisten bevorzugte Wert für K ist 5.
• Ein sehr niedriger Wert für K wie K = 1 oder K = 2 kann verrauscht sein und zu den Auswirkungen von Ausreißern im Modell führen.
• Große Werte für K sind gut, können jedoch einige Schwierigkeiten verursachen.

Vorteile des KNN-Algorithmus:

• Es ist einfach zu implementieren.
• Es ist robust gegenüber verrauschten Trainingsdaten.
• Es kann effektiver sein, wenn die Trainingsdaten groß sind.

Nachteile des KNN-Algorithmus:

• Muss immer den Wert von K bestimmen, der einige Zeit komplex sein kann.
• Die Berechnungskosten sind hoch, da der Abstand zwischen den Datenpunkten für alle Trainingsmuster berechnet wird .

Python-Implementierung des KNN-Algorithmus

Um die Python-Implementierung des K-NN-Algorithmus durchzuführen, verwenden wir dasselbe Problem und denselben Datensatz, in dem wir verwendet haben Logistische Regression. Aber hier werden wir die Leistung des Modells verbessern. Unten finden Sie die Problembeschreibung:

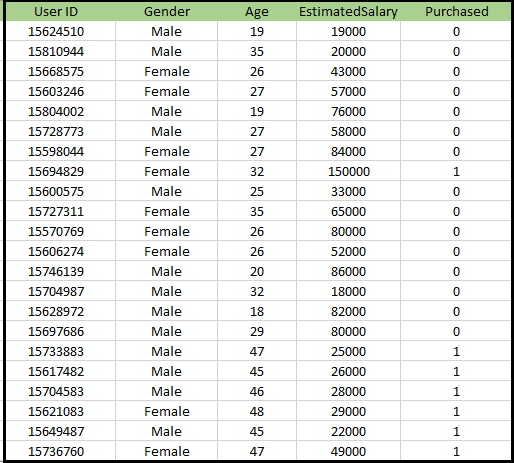
Problem für den K-NN-Algorithmus: Es gibt eine Autoherstellerfirma, die ein neues SUV-Auto hergestellt hat.Das Unternehmen möchte die Anzeigen den Nutzern geben, die am Kauf dieses SUV interessiert sind. Für dieses Problem haben wir einen Datensatz, der Informationen mehrerer Benutzer über das soziale Netzwerk enthält. Der Datensatz enthält viele Informationen, aber das geschätzte Gehalt und Alter, das wir für die unabhängige Variable berücksichtigen, und die gekaufte Variable für die abhängige Variable. Unten ist der Datensatz:

Schritte zum Implementieren des K-NN-Algorithmus:

• Datenvorverarbeitungsschritt
• Anpassen des K-NN-Algorithmus an den Trainingssatz
• Vorhersage des Testergebnisses
• Testgenauigkeit des Ergebnisses (Erstellung einer Verwirrungsmatrix)
• Visualisierung des Testergebnises.

Datenvorverarbeitungsschritt:

Der Datenvorverarbeitungsschritt bleibt genau derselbe wie die logistische Regression. Nachfolgend finden Sie den Code dafür:

Durch Ausführen des obigen Codes wird unser Datensatz in unser Programm importiert und gut vorverarbeitet. Nach der Skalierung der Funktionen sieht unser Testdatensatz folgendermaßen aus:

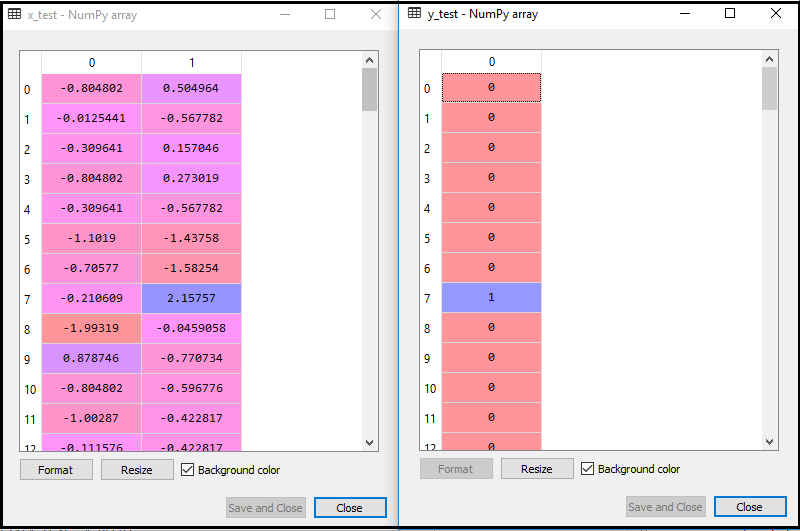
Aus der obigen Ausgabe im Alter können wir sehen, dass unsere Daten erfolgreich skaliert werden.

• Anpassen des K-NN-Klassifikators an die Trainingsdaten:
  Jetzt passen wir den K-NN-Klassifikator an die Trainingsdaten an. Dazu importieren wir die KNeighborsClassifier-Klasse der Sklearn Neighbors-Bibliothek. Nach dem Importieren der Klasse erstellen wir das Classifier-Objekt der Klasse. Der Parameter dieser Klasse lautet
  • n_neighbors: Zum Definieren der erforderlichen Nachbarn des Algorithmus. Normalerweise dauert es 5.
  • metric = „minkowski“: Dies ist der Standardparameter und entscheidet über den Abstand zwischen den Punkten.
  • p = 2: Entspricht dem Standard Euklidische Metrik.

  Und dann passen wir den Klassifikator an die Trainingsdaten an. Unten ist der Code dafür:

Ausgabe: Durch Ausführen des obigen Codes erhalten wir die Ausgabe als:

• Vorhersage des Testergebnisses: Um das Testergebnis vorherzusagen, erstellen wir einen y_pred-Vektor wie in Logistic Regression. Unten ist der Code dafür:

Ausgabe:

Die Ausgabe für den obigen Code lautet:

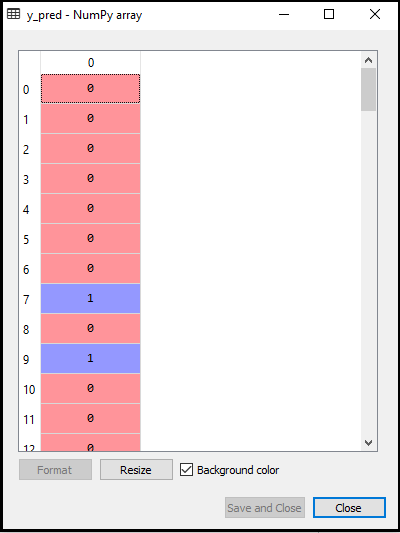
• Erstellen der Verwirrungsmatrix:
  Jetzt erstellen wir die Verwirrungsmatrix für unser K-NN-Modell, um die Genauigkeit des Klassifikators zu überprüfen. Unten ist der Code dafür:

Im obigen Code haben wir die Funktion confusion_matrix importiert und mit der Variablen cm aufgerufen.

Ausgabe: Durch Ausführen des obigen Codes erhalten wir die folgende Matrix:

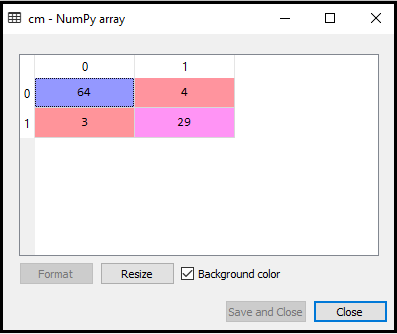
Im obigen Bild sehen wir Es gibt 64 + 29 = 93 korrekte Vorhersagen und 3 + 4 = 7 falsche Vorhersagen, während es in der logistischen Regression 11 falsche Vorhersagen gab. Wir können also sagen, dass die Leistung des Modells durch Verwendung des K-NN-Algorithmus verbessert wird.

• Visualisierung des Trainingssatzergebnisses:
  Nun werden wir das Trainingssatzergebnis für K visualisieren -NN Modell. Der Code bleibt bis auf den Namen des Diagramms derselbe wie bei der logistischen Regression. Unten ist der Code dafür:

Ausgabe:

Durch Ausführen des obigen Codes erhalten wir die folgende Grafik:

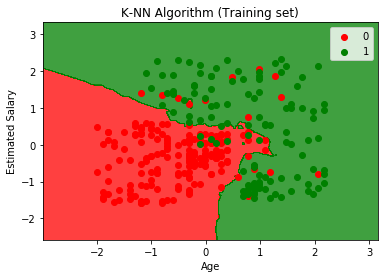
Das Ausgabediagramm unterscheidet sich von dem Diagramm, das wir in der logistischen Regression erstellt haben. Dies kann in den folgenden Punkten verstanden werden:

• Wie wir sehen können, zeigt das Diagramm den roten und den grünen Punkt. Die grünen Punkte gelten für die Variable „Gekauft“ (1) und die roten Punkte für die Variable „Nicht gekauft“ (0).
• Der Graph zeigt eine unregelmäßige Grenze, anstatt eine gerade Linie oder eine Kurve zu zeigen, da es sich um einen K-NN-Algorithmus handelt, d. h. um den nächsten Nachbarn zu finden.
• In der Grafik wurden Benutzer in die richtigen Kategorien eingeteilt, da sich die meisten Benutzer, die den SUV nicht gekauft haben, im roten Bereich und Benutzer, die den SUV gekauft haben, im grünen Bereich befinden.
• Die Grafik zeigt ein gutes Ergebnis, aber es gibt immer noch einige grüne Punkte im roten Bereich und rote Punkte im grünen Bereich. Dies ist jedoch kein großes Problem, da durch dieses Modell verhindert wird, dass Probleme auftreten.
• Daher ist unser Modell gut trainiert.
• Visualisierung des Testergebnises:
  Nach dem Training des Modells werden wir das Ergebnis nun testen, indem wir einen neuen Datensatz einfügen, d. h. Testdatensatz. Der Code bleibt bis auf einige geringfügige Änderungen gleich: x_train und y_train werden durch x_test und y_test ersetzt.
  Nachfolgend finden Sie den Code dafür:

Ausgabe:

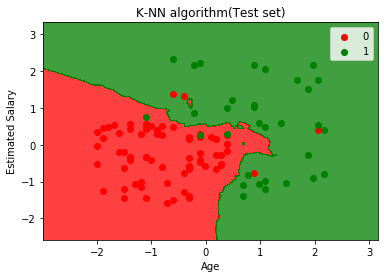
Das obige Diagramm zeigt die Ausgabe für den Testdatensatz. Wie wir in der Grafik sehen können, ist die vorhergesagte Ausgabe gut gut, da die meisten roten Punkte im roten Bereich liegen und Die meisten grünen Punkte befinden sich im grünen Bereich.

Es gibt jedoch nur wenige grüne Punkte im roten Bereich und einige rote Punkte im grünen Bereich. Dies sind also die falschen Beobachtungen, die wir in der Verwirrungsmatrix beobachtet haben (7 Falsche Ausgabe).