Solutions (한국어)
ColligativeProperties
Vapor PressureDepression
물리적 속성은 두 가지 범주로 나눌 수 있습니다. 광범위한 특성 (예 : 질량 및 부피)은 샘플의 크기에 따라 다릅니다. 집중적 특성 (예 : 밀도 및 농도)은 물질의 특징적인 특성이며 연구중인 샘플의 크기에 의존하지 않습니다. 이 섹션에서는 시스템의 집약적 속성의 하위 집합 인 세 번째 범주를 소개합니다. colligativeproperties로 알려진이 세 번째 범주는 솔루션에만 적용 할 수 있습니다. 정의에 따르면 용액의 특성 중 하나는 용질의 정체가 아니라 용액의 용질과 용매 입자 수의 비율에만 의존하는 경우 결합 속성입니다.
솔루션의 물리적 특성 중 거의 충돌 특성이 없습니다. 이 제한된 물리적 특성 집합의 예로, 용액을 형성하기 위해 용질을 추가 할 때 용매의 증기압에 어떤 일이 발생하는지 고려해 보겠습니다. Po를 순수한 액체의 증기압으로 정의합니다. 
용매 및 용질이 추가 된 후 용매의 증기압으로 P.
Po = 순수한 액체의 증기압 또는 용매
P = 용액 내 용매의 증기압
액체의 온도가 끓는점 이하일 때 포인트, 우리는 액체에서 빠져 나가 기체를 형성 할 수있는 분자는 액체 표면 근처에있는 분자들 뿐이라고 가정 할 수 있습니다.
용질이 용매에 추가되면 아래 그림과 같이 일부 용질 분자가 액체 표면 근처의 공간을 차지합니다. 용질이 용매에 용해되면 표면 근처의 용매 분자 수가 감소하고 용매의 증기압이 감소합니다.
이것은 기체상의 용매 분자가 응축되어 액체를 형성하는 속도에 영향을주지 않습니다. 그러나 액체의 용매 분자가 기체 상태로 빠져 나갈 수있는 속도를 감소시킵니다. 결과적으로 용액에서 빠져 나가는 용매의 증기압은 순수한 용매의 증기압보다 작아야합니다.
| P | < | Po | ||
| 증기압 용매 용액 위 |
순수 용매의 증기압 |
1887 년에서 1888 년 사이 Francois-Marie Raoult는 용액의 증기압이 용매의 몰 분율에 순수한 액체의 증기압을 곱한 것과 같습니다.
| P | = | 용제 Po | ||||
| 증기압 솔벤트 용액 위 |
순수 용매의 증기압 |
라울 트의 법칙으로 알려진이 방정식은 이해하기 쉽습니다. 용매가 순수하고 용매의 몰분율이 1 일 때 P는 Po와 같습니다. 용매의 몰분율이 작아짐에 따라 , 용액에서 빠져 나가는 용매의 증기압 또한 더 작아집니다.
현재 용매가 측정 가능한 증기압을 가질 수있을만큼 충분히 휘발성 인 용액의 유일한 성분이라고 가정 해 봅시다. 이것이 사실이라면, 용액의 증기압은 용액에서 배출되는 용매의 증기압과 같을 것입니다. Raoult의 법칙은 용매의 몰 분율이 감소함에 따라 순수한 용매의 증기압과 용액 사이의 차이가 증가 함을 시사합니다.
아솔 루트를 용매에 첨가 할 때 발생하는 증기압의 변화는 다음과 같습니다. 따라서 colligative property. 만약 그것이 용질의 몰 분율에 의존한다면, 용질의 정체가 아닌 용액에서 용질의 입자 수와 용질의 비율에 의존해야합니다.
끓는점 상승 및 어는점 강하
아래 그림은 용질이 용매의 증기압을 낮추는 사실의 결과를 보여줍니다. 이 상 다이어그램에서 점 B와 C를 연결하는 선은 순수한 용매와 증기가 평형을 이루는 온도와 압력의 조합을 포함합니다. 따라서이 선의 각 점은 해당 온도에서 순수한 용매의 증기압을 나타냅니다.이 그림의 점선은 특성을 설명합니다. 아솔 루트를 용매에 용해시켜 얻은 용액.주어진 온도에서 용액에서 빠져 나가는 용매의 증기압은 순수한 용매의 증기압보다 작습니다. 따라서 점선은 실선 아래에 있습니다.
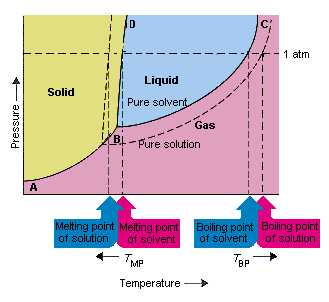
용질이 용매에 첨가 될 때 발생하는 용매의 증기압은 끓는점을 증가시키고 용액의 융점을 감소시킵니다.
이 그림에 따르면 용액은 순수한 용매와 같은 온도에서 끓을 수 없습니다. 증기압이 용액에서 빠져 나가는 용매가 특정 온도에서 순수한 용매의 증기압보다 작 으면 용액이 끓기 전에 더 높은 온도로 가열해야합니다. 따라서 용액을 형성하는 데 사용될 때 발생하는 용매의 증기압이 낮아집니다. 액체의 끓는점을 증가시킵니다.
상 다이어그램이 도입되었을 때, 삼중점은 기체, 액체 및 고체가 동시에 존재할 수있는 온도와 압력의 유일한 조합으로 정의되었습니다. 위 그림은 용액의 삼중점이 순수한 용매의 삼중점보다 낮은 온도에서 발생한다는 사실 자체로 삼중점의 변화는 중요하지 않지만 용액이 얼거나 녹는 온도의 변화를 초래합니다. 왜, 우리는 조심해야 위상 다이어그램에서 고체와 액체 영역을 분리하는 선에 완전히 있습니다. 물질의 융점이 압력에 매우 민감하지 않기 때문에이 선은 거의 수직입니다.
용질을 용매에 첨가해도 용융점이 압력에 의존하는 방식은 바뀌지 않습니다. 따라서 용액의 고체 및 액체 영역을 분리하는 선은 순수한 용매에 대해 동일한 기능을 수행하는 선과 평행합니다. 그러나이 선은 용액의 삼중점을 통과해야하지만, 아솔 루트가 용매에 용해 될 때 발생하는 삼중점의 감소는 용액의 융점을 감소시킵니다.
위 그림은 용질이 용매에 용해 될 때 발생하는 증기압의 변화는 용매의 융점과 끓는점의 변화로 이어집니다. , 용매의 끓는점과 녹는 점의 변화도 결합 속성입니다.
ColligativeProperties 계산
악마에게 가장 좋은 방법 colligativeproperties의 중요성은 Raoult의 법칙의 결과를 조사하는 것입니다. 용액에서 빠져 나가는 용매의 증기압이 용매의 몰 분율에 비례한다는 사실을 발견했습니다.
P = CsolventPo
그러나 용매의 증기압은 충돌 속성이 아닙니다. 용질이 용매에 첨가 될 때 발생하는 증기압의 변화 만이 용액의 응집 특성에 포함될 수 있습니다.
압력은 상태 함수이기 때문에 용매에 용질을 첨가 할 때 발생하는 용매의 증기압의 변화는 순수한 용매의 증기압과 용매의 증기압의 차이로 정의 할 수 있습니다. 솔루션에서 탈출.
P = Po-P
이 방정식에 Raoult의 법칙을 대입하면 다음과 같은 결과를 얻을 수 있습니다.
P = Po-Csolvent Po = (1-Csolvent) Po
이 방정식은 용질의 몰분율과 용매의 몰분율 사이의 관계를 기억하여 단순화 할 수 있습니다.
Csolute + Csolvent = 1
대체 P를 정의하는 방정식에 대한 관계는 라울 트 법칙의 또 다른 형태를 제공합니다.
P = CsolutePo
이 방정식은 용질이 용질에 첨가 될 때 발생하는 용제의 증기압 변화가 용질의 몰 분율에 비례 함을 상기시킵니다. 용매에 더 많은 용매가 용해됨에 따라 용매의 증기압이 감소하고 용매의 증기압의 변화가 증가합니다.
용질이 용매에 첨가 될 때 발생하는 용매의 끓는점 (TBP)의 변화는 용매의 증기압의 변화로 인해 발생하기 때문에 끓는점의 변화 크기도 비례합니다. 용질의 몰분율.
TBP = kbsolute
희석 용액에서 용질의 몰 분율은 다음과 같이 용액의 몰 농도에 비례합니다. 아래 그림.
용질이 용매에 첨가 될 때 발생하는 끓는점 높이의 크기를 설명하는 방정식은 따라서 종종 다음과 같이 작성됩니다.
TBP = kbm
여기에서 TBP는 끓는점 고도입니다. 용질이 용매에 용해 될 때 발생하는 끓는점의 변화 및 kb는 용매에 대한 몰 끓는점 상승 상수로 알려진 비례 상수입니다.
용질이 용매에 첨가 될 때 용매의 빙점 (또는 융점)에 어떤 일이 발생하는지 설명하기 위해 유사한 방정식을 쓸 수 있습니다.
TFP = -kfm
이 방정식에서 TFP는 빙점입니다. 강하 용질이 용매에 용해 될 때 발생하는 빙점의 변화이며 kfis는 용매에 대한 몰랄 빙점 강하 상수입니다. 이 방정식에서 음의 기호는 용질이 첨가 될 때 용매의 어는점이 감소 함을 나타냅니다.
kf 및 kbas 값과 여러 순수 용매에 대한 빙점 및 끓는점은 아래 표에 나와 있습니다.
빙점 강하 상수
끓는점 고도 상수
문제 6 :
유황 35.5g이 CS2 100.0g에 용해되어 끓는점이 49.48oC 인 용액을 생성하는 경우 황의 분자량을 계산합니다.
연습 문제 6에 대한 답을 확인하려면 여기를 클릭하십시오.
연습 문제 6의 해결책을 보려면 여기를 클릭하십시오.
연습 문제 7 :
당 30.0g의 아세트산을 포함하는 용액의 경우 아세트산의 분자량을 결정합니다. 물 킬로그램은 -0.93oC에서 얼어 있습니다. 이 결과는 아세트산이 화학식 CH3CO2H를 갖는다는 가정과 일치합니까?
연습 문제 7에 대한 답을 확인하려면 여기를 클릭하십시오.
연습 문제 7에 대한 해결책을 보려면 여기를 클릭하십시오.
연습 문제 7의 계산에서 어떤 일이 염산과 같은 더 강한 산으로 반복 되었습니까?
실습 문제 8 :
벤젠에 용해 된 0.100m HCl 용액의 빙점 강하가 0.512 ° C 인 반면 물에 용해 된 0.100m HCl 용액의 빙점 강하가 0.352 ° C 인 이유를 설명하십시오.
연습 문제 8에 대한 답을 확인하려면 여기를 클릭하십시오.
1884 년 Jacobus Henricus van “t Hoff는 물에 용해 될 때 해리되는 화합물 용액의 결합 특성을 설명하기 위해 빙점 강하 및 끓는점 상승 표현에 대한 또 다른 용어를 도입했습니다.
TFP =- kf (i) m
0.100 m HCl 용액의 빙점 강하에 대한 실험 값을이 방정식에 대입하면 i 항에 대한 값이 1.89가됩니다. HCl이 물에서 분리되지 않으면 i가 1이됩니다. 완전히 해리되면 나는 2가됩니다. 1.89의 실험 값은이 용액에서 HCl 분자의 95 % 이상이 해리됨을 의미합니다.
연습 문제 9 :
0.60g의 아세트산이 200g의 벤젠에 용해되어 벤젠의 어는점을 5.40 ° C로 낮추는 용액을 형성하는 이유를 설명하십시오.
여기를 클릭하여 답을 확인하십시오. 연습 문제 9
삼투압
1784 년 프랑스의 물리학 자이자 성직자 인 Jean AntoineNollet은 농축 된 알코올 용액으로 채워진 돼지의 방광이 물에 담그면 팽창한다는 것을 발견했습니다. 방광은 물 분자가 용액에 들어가는 것을 허용하는 반투과성 막 역할을했지만 알코올 분자는 다른 방향으로 움직이지 못하게했습니다. 용액을 희석하기 위해 막을 통해 용액의 한 성분이 이동하는 것을 삼투라고하며, 이것이 생성하는 압력을 삼투압 ()이라고합니다.
삼투압은 아래 그림과 같은 장치로 증명할 수 있습니다. 반투막이 엉겅퀴 관의 열린 끝 부분에 묶여 있습니다. 그런 다음 튜브를 물에 설탕 또는 알코올 용액으로 부분적으로 채우고 물 비커에 담근다. 물은 중력으로 인해 물기둥에 가해지는 압력이 막을 통해 물을 구동하는 테 삼투압 균형을 맞출 때까지 튜브로 흘러 들어갑니다.
물이 흐릅니다. 이 용액의 기둥을 아래로 당기는 중력이 막을 통해 물을 밀어내는 삼투압과 균형을 이룰 때까지 알코올 용액을 희석하는 반투막.
Raoult가 용액의 증기압과 순수한 용매의 증기압 사이의 관계를 발견 한 같은 해 Jacobus Henricus van “t Hoff는 희석 용액 ()의 삼투압이 이상 기체 방정식과 유사한 방정식을 따른다는 것을 발견했습니다.
 |
= | nRT | ||
| V |
이 방정식은 삼투압이 충돌 속성의 또 다른 예임을 시사합니다. 압력은 용질 입자의 정체가 아닌 용액 부피에 대한 용질 입자 수의 비율에 따라 달라집니다. n / V 또한 삼투압의 크기를 상기시켜줍니다.이 방정식에 따르면 1.00 M s olution은 0oC에서 22.4 atm의 삼투압을가집니다.
이것은 1.00M 용액이 670 인치 (약 56 피트) 높이의 물 기둥을 지탱할 수 있어야 함을 의미합니다. !
생물 학자와 생화학 자들은 종종 세포의 구성 요소를 분리 할 때 삼투압을 이용합니다. 세포 내 액체보다 훨씬 높은 농도의 이온을 포함하는 수용액에 세포를 첨가하면 세포가 수축하여 세포막이 부러 질 때까지 세포막을 통과하여 물이 세포를 떠납니다. 또는 이온 강도가 훨씬 작은 용액에 세포를 넣을 때 물이 세포에 쏟아지고 세포막이 터질 때까지 세포가 팽창합니다.