두 개 이상의 그룹을 비교하기위한 모수 및 비모수 테스트

통계 : 모수 및 비모수 테스트

이 섹션 다룹니다.

• 테스트 선택
• 매개 변수 테스트
• 비모수 테스트

테스트 선택

통계 테스트를 선택할 때 가장 중요한 질문은 “주요 연구 가설은 무엇입니까?”입니다. 어떤 경우에는 가설이 없습니다. 수사관은 “무엇이 있는지”보고 싶어합니다. 예를 들어, 유병률 연구에서 테스트 할 가설이 없으며 연구의 규모는 조사자가 유병률을 얼마나 정확하게 결정하기를 원하는지에 따라 결정됩니다. 가설이 없으면 통계 검정이 없습니다. 어떤 가설이 확증 적인지 (즉, 일부 가정 된 관계를 테스트하고 있음) 탐색 적 (데이터에 의해 제 안됨)인지를 선험적으로 결정하는 것이 중요합니다. 단일 연구는 전체 가설을 뒷받침 할 수 없습니다. 현명한 계획은 확증 가설의 수를 엄격하게 제한하는 것입니다. 데이터가 제시 한 가설에 대한 통계적 검정을 사용하는 것은 타당하지만, P 값은 지침으로 만 사용해야하며 결과는 후속 연구에서 확인 될 때까지 임시로 처리해야합니다. 유용한 가이드는 Bonferroni 수정을 사용하는 것입니다. 이는 단순히 n 개의 독립적 인 가설을 테스트하는 경우 0.05 / n의 유의 수준을 사용해야한다는 것입니다. 따라서 두 개의 독립적 인 가설이있는 경우 P < 0.025 인 경우에만 결과가 중요하다고 선언됩니다. 테스트가 거의 독립적이기 때문에 이것은 매우 보수적 인 절차입니다. 즉, 귀무 가설을 기각 할 가능성이 거의없는 절차입니다. 조사자는 “데이터가 독립적입니까?”라고 질문해야합니다. 이것은 결정하기 어려울 수 있지만 경험상 동일한 개인 또는 일치하는 개인에 대한 결과는 독립적이지 않습니다. 따라서 교차 시험 또는 대조군이 연령, 성별 및 사회적 계급별로 사례와 일치하는 사례 대조 연구의 결과는 독립적이지 않습니다.

• 분석은 설계를 반영해야합니다. , 따라서 일치하는 디자인에 일치하는 분석이 이어져야합니다.
• 시간이 지남에 따라 측정 된 결과는 특별한주의가 필요합니다. 통계 분석에서 가장 흔한 실수 중 하나는 상관 변수를 독립적 인 것처럼 취급하는 것입니다. 예를 들어, 일부 사람들이 각 다리에 궤양이있는 다리 궤양의 치료를보고 있다고 가정 해 보겠습니다. 30 명의 궤양을 가진 20 명의 피험자가있을 수 있지만, 한 사람의 각 다리에있는 궤양의 상태는 개인의 건강 상태 및 분석에 의해 영향을받을 수 있기 때문에 독립적 인 정보의 수는 20 개입니다. 궤양을 독립적 인 관찰로 간주하는 것은 올바르지 않습니다. 쌍을 이루는 혼합 데이터와 쌍을 이루지 않는 데이터를
  올바르게 분석하려면 통계 전문가에게 문의하십시오.

다음 질문은 “어떤 유형의 데이터가 측정되고 있습니까?”입니다. 사용 된 테스트는 데이터에 의해 결정되어야합니다. 일치 또는 쌍을 이루는 데이터에 대한 테스트의 선택은 표 1에 설명되어 있고 표 2에 독립 데이터에 대한 내용이 설명되어 있습니다.

표 1 쌍을 이루거나 일치하는 관찰에서 통계 테스트 선택

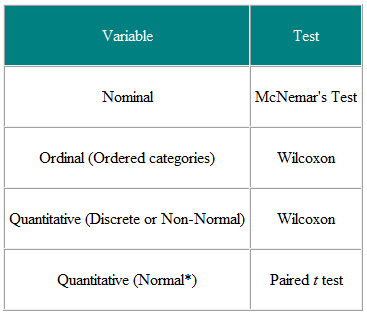
입력 변수와 결과 변수를 결정하는 것이 유용합니다. 예를 들어, 임상 시험에서 입력 변수는 치료 유형 (명목 변수)이고 결과는 아마도 정규 분포 일 수있는 일부 임상 측정 일 수 있습니다. 필요한 테스트는 t- 테스트입니다 (표 2). 그러나 입력 변수가 연속적 (예 : 임상 점수)이고 결과가 명목 (예 : 치료되었거나 치료되지 않음)이면 로지스틱 회귀 분석이 필수 분석입니다. 이 경우 t- 검정은 도움이 될 수 있지만 우리에게 필요한 것, 즉 주어진 임상 점수 값에 대한 치료 가능성을 제공하지는 않습니다. 또 다른 예로, 무작위 표본을 대상으로 일반 개업의가 잘하고 있다고 생각하는지 5 점 척도로 질문하고 여성의 의견이 더 높은지 확인하는 단면 연구가 있다고 가정합니다. 남성보다 일반의의. 입력 변수는 성별이며 명목입니다. 결과 변수는 5 점 순서 척도입니다. 각 개인의 의견은 서로 독립적이므로 독립적 인 데이터를 가지고 있습니다. 표 2에서 추세에 대해서는 χ2 테스트를 사용하거나 동점을 수정 한 Mann-Whitney U 테스트를 사용해야합니다 (NB는 두 개 이상 값이 동일하므로 엄격하게 증가하는 순위 순서가 없습니다.이 경우 동률 값에 대한 순위를 평균화 할 수 있습니다. 그러나 일부 사람들은 일반 진료의를 공유하고 다른 사람들은 그렇지 않은 경우 데이터는 그렇지 않습니다. 독립적이고보다 정교한 분석이 필요합니다. 이러한 표는 지침으로 만 고려되어야하며 각 사례는 그 장점을 고려해야합니다.

표 2 독립 관찰을위한 통계 테스트 선택

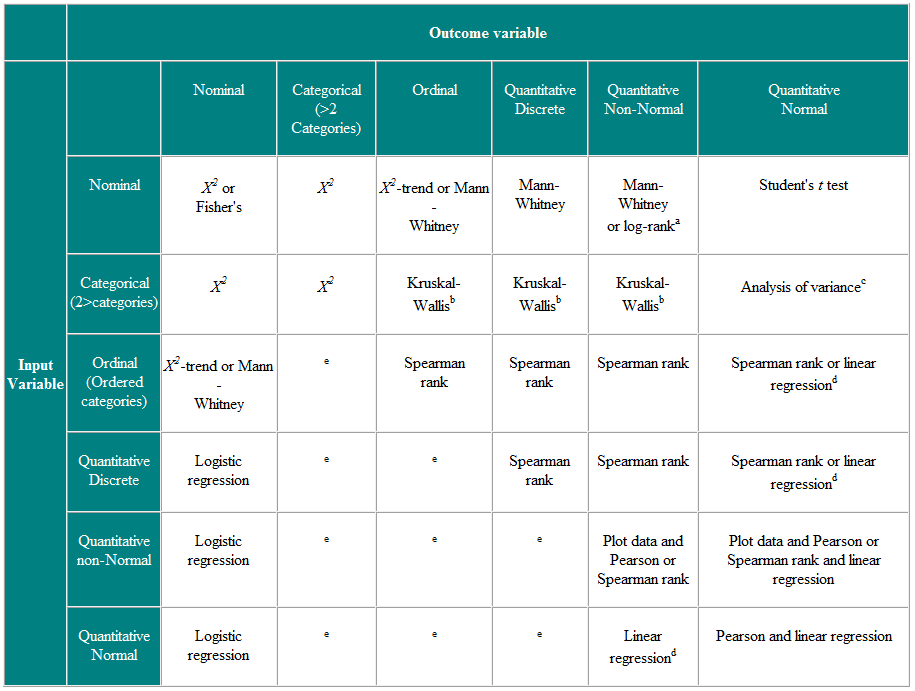
a 데이터가 검열 된 경우. b Kruskal-Wallis 검정은 세 개 이상의 그룹에 대한 순서 형 또는 비정규 변수를 비교하는 데 사용되며 Mann-Whitney U 검정의 일반화입니다. c 분산 분석은 일반적인 기술이며 하나의 버전 (일원 분산 분석)은 두 개 이상의 그룹에 대한 정규 분포 변수를 비교하는 데 사용되며 Kruskal-Wallistest와 모수 적 동등합니다. d 결과 변수가 종속 변수 인 경우 잔차 (관측 된 값과 회귀에서 예측 된 응답 간의 차이)가 그럴듯하게 정규 분포를 따르는 경우 독립 변수의 분포는 중요하지 않습니다. e 이러한 상황을 처리하기위한 포아송 회귀와 같은 더 많은 고급 기술이 있습니다. 그러나 특정 가정이 필요하며 종종 결과 변수를이 분화하거나 연속으로 취급하는 것이 더 쉽습니다.

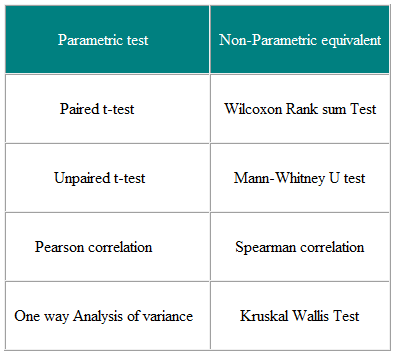
모수 적 검정은 표본이 추출되는 모집단 분포의 매개 변수에 대한 가정을 만드는 것입니다. . 이것은 종종 모집단 데이터가 정규 분포를 따른다는 가정입니다. 비모수 테스트는 “분포가 필요하지 않습니다”. 따라서 비정규 변수에 사용할 수 있습니다. 표 3은 여러 모수 테스트에 해당하는 비모수 테스트를 보여줍니다.

표 3 Parametric 및 두 개 이상의 그룹을 비교하기위한 비모수 테스트

비모수 테스트는 비정상적으로 분산 된 데이터와 정규 분포 데이터이므로 항상 사용하지 않는 이유는 무엇입니까?

모든 경우에 비모수 테스트를 사용하는 것이 현명 해 보이므로 정규성 테스트의 번거 로움을 줄일 수 있습니다. 매개 변수 테스트가 선호됩니다. 그러나 다음과 같은 이유가 있습니다.

1. 우리는 유의성 검정에만 관심이 거의 없습니다. 표본을 가져온 모집단에 대해 말하고 싶습니다.이 작업을 수행하는 것이 가장 좋습니다.
매개 변수 및 신뢰 구간의 추정치.

2. 비모수 테스트로 유연한 모델링을 수행하는 것은 어렵습니다. 예를 들어 다중 회귀.

3. 일반적으로 모수 검정은 비모수 검정보다 통계적 검정력이 더 높습니다. 즉, 실제로 존재하는 경우
중요한 차이를 감지 할 가능성이 더 높습니다.

비모수 테스트는 중앙값을 비교합니까?

Mann-Whitney U 테스트는 실제로 중앙값의 차이에 대한 테스트입니다. 그러나 두 그룹의 중앙값은 같지만 Mann-Whitney U 검정이 중요 할 수 있습니다. 각각 100 개의 관측치가있는 두 그룹에 대한 다음 데이터를 고려하십시오. 그룹 1:98 (0), 1, 2; 그룹 2:51 (0), 1, 48 (2). 두 경우의 중앙값은 0이지만 Mann-Whitney 테스트 P < 0.0001입니다. 두 그룹의 차이가 단순히 위치의 이동 (즉, 한 그룹의 데이터 분포가 다른 그룹에서 고정 된 양만큼 단순히 이동 됨)이라는 추가 가정을 할 준비가되어있는 경우에만 다음과 같이 말할 수 있습니다. 검정은 중앙값의 차이에 대한 검정입니다. 그러나 그룹의 분포가 동일한 경우 위치 이동은 중앙값과 평균을 같은 양만큼 이동하므로 중앙값의 차이는 평균의 차이와 동일합니다. 따라서 Mann-Whitney U 검정은 평균 차이에 대한 검정이기도합니다. Mann- Whitney U 테스트는 t- 테스트와 어떤 관련이 있습니까? 데이터 자체가 아닌 데이터의 순위를 두 개의 샘플 t- 테스트 프로그램에 입력하면 얻은 P 값은 Mann-Whitney U 테스트에서 생성 된 값과 매우 비슷합니다.