이산 랜덤 변수의 분포를 결정하기 위해 PMF 또는 CDF를 제공 할 수 있습니다. 연속 확률 변수의 경우 CDF가 잘 정의되어 있으므로 CDF를 제공 할 수 있습니다. 그러나 PMF는 모든 $ x \ in \ mathbb {R} $에 대해 연속 랜덤 변수 $ P (X = x) = 0 $에 대해 연속 랜덤 변수에 대해 작동하지 않습니다. 대신 일반적으로 확률 밀도 함수 (PDF)를 정의 할 수 있습니다. PDF는 확률 질량이 아닌 확률 밀도입니다. 개념은 물리학의 질량 밀도와 매우 유사합니다. 단위는 단위 길이 당 확률입니다. PDF에 대한 느낌을 얻으려면 연속 랜덤 변수 $ X $를 고려하고 $ f_X (x) $ 함수를 다음과 같이 정의하십시오 (한계가있는 경우) : $$ f_X (x) = \ lim _ {\ Delta \ rightarrow 0 ^ +} \ frac {P (x

$$ f_X (x) = \ lim _ {\ Delta \ rightarrow 0} \ frac {F_X (x + \ Delta) -F_X (x)} {\ Delta} $$ $$ = \ frac {dF_X (x)} {dx} = F ” _X (x), \ hspace {20pt} \ textrm {if} F_X (x) \ textrm {은} x. $$

에서 미분 할 수 있습니다.

따라서 다음과 같은 정의가 있습니다. 연속 랜덤 변수의 PDF :

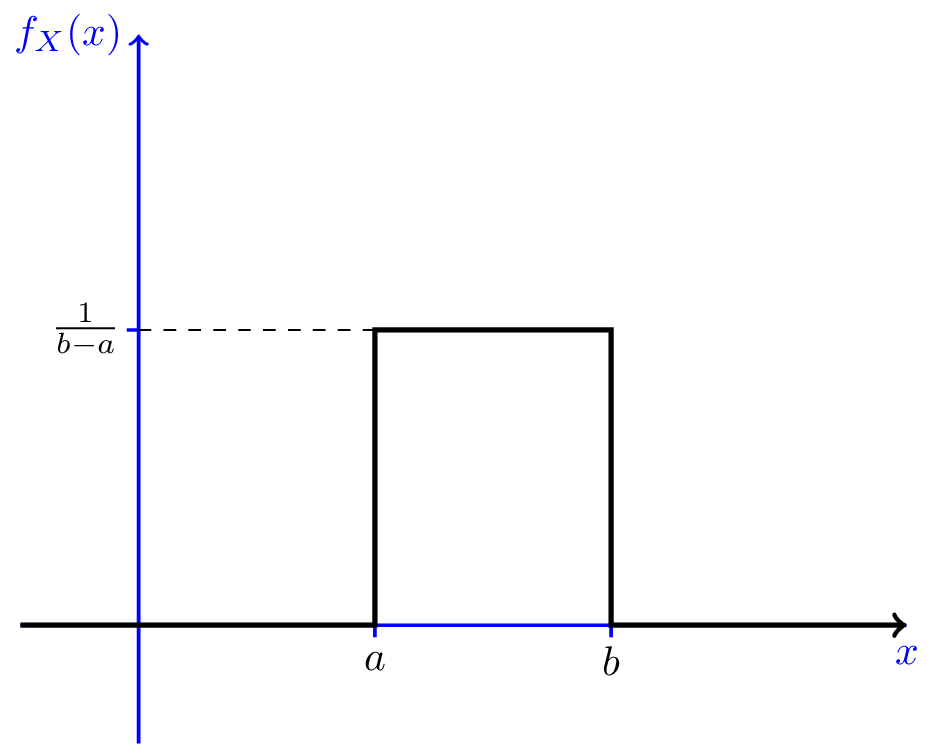
예제
$ X $를 다음 PDF \ begin {equation} \ nonumber f_X (x) =를 갖는 연속 랜덤 변수가되도록합니다. \ left \ {\ begin {array} {ll} ce ^ {-x} & \ quad x \ geq 0 \\ 0 & \ quad \ text {otherwise} \ end {array} \ right. \ end {equation} 여기서 $ c $는 양의 상수.

1. $ c $ 찾기
2. X, $ F_X (x) $의 CDF 찾기
3. $ P (1 찾기

범위