수직 점근선은 출력이 매우 크거나 매우 작을 때 그래프의 동작을 설명하는 반면, 수평 점근선은 그래프의 동작을 다음과 같이 설명하는 데 도움이됩니다. 입력이 매우 커지거나 작아집니다. 다항식의 끝 동작은 선행 용어의 동작을 반영합니다. 마찬가지로, 유리 함수의 끝 동작은 분자 및 분모 함수의 선행 항의 비율을 반영합니다.

수평 점근선을 확인할 때 세 가지 뚜렷한 결과가 있습니다.

사례 1 : 분자의 분모 정도가 >이면 y = 0에 수평 점근선이 있습니다.

사례 2 : 분자의 분모 정도가 <이면 경사 점근선이됩니다.

합리적 함수의 그래프는 수직 점근선을 가로 지르지 않지만 그래프는 다음과 같이 가로 또는 기울어 지거나 가로 지르지 않을 수 있습니다. ymptote. 또한 합리적 함수의 그래프는 많은 수직 점근선을 가질 수 있지만 그래프는 최대 하나의 수평 (또는 경사) 점근선을 가질 것입니다.

분자의 차수가 더 클 경우 유의해야합니다. 분모의 정도가 하나 이상인 경우 그래프의 끝 동작은 감소 된 끝 동작 비율의 동작을 모방합니다. 예를 들어 함수가있는 경우

끝 동작 포함

그래프의 최종 동작은 선행 계수가 양수인 짝수 다항식의 동작과 유사합니다.

예 9 : 수평 및 수직 점근선 식별

함수의 수평 및 수직 점근선 찾기

fleft (xright) = frac {left (x-2right) left (x + 3right)} {left (x-1right) left (x + 2right) left (x-5right)} \

해결책

먼저,이 함수에는 공통 요소가 없으므로 제거 가능한 불연속성이 없습니다.

분모가 0 일 때 함수는 수직 점근선을 가지므로 함수가 정의되지 않습니다. 분모는 x = 1, -2, text {및} 5 \에서 0이되며 이러한 값에서 수직 점근선을 나타냅니다.

분자는 차수가 2이고 분모는 차수가 3입니다. 분모의 분모가 분자의 차수보다 크면 분모가 분자보다 빠르게 증가하여 입력이 커지면 출력이 0이되고 xto pm infty, fleft (xright)가 0 \이됩니다. 이 함수는 y = 0 \에 수평 점근선을 갖습니다.

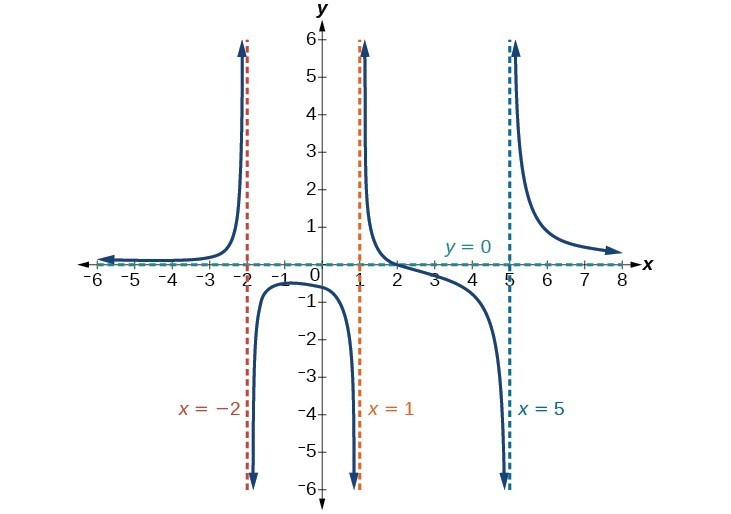
그림 15